How To Build And Analyze A Parallel Circuit
Theory
In the last Hub, we looked at series circuits and saw how they have a common current value through all the component resistors and distribute the voltage drops proportionately to their respective resistances. In this Hub, we'll see how a parallel circuit has a common voltage value across all the component resistors and how it distributes the input current among the resistors depending on the resistor's values. There is also a different formula for determining the overall equivalent resistance of a parallel resistive circuit than is used for determining the overall equivalent resistance of a series circuit. While the equivalent resistance of a series circuit is the sum of all the component resistors, the equivalent resistance of a parallel circuit is always smaller than the smallest of any of the parallel resistors!
Conductances Add Up
With series resistors, you find the equivalent resistance by simply adding the series resistors. With parallel resistors, however, the way to find the equivalent resistance is to add up the reciprocals of the resistors (called the conductances) and then take the reciprocal of that sum to finally get the equivalent resistance. Shown below is a schematic with the formula relating the equivalent resistance to the parallel resistances.
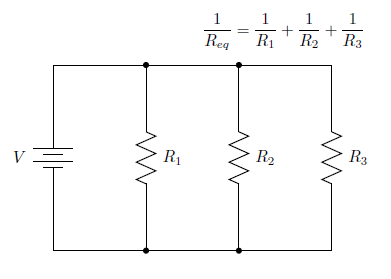
One common special case that has its own convenient formula is the case of two resistors in parallel. Applying the above formula, you get
1/Req = 1/R1 + 1/R2
Taking the reciprocal of both sides, you get
Req = 1/( 1/R1 + 1/R2)
That sum of reciprocals in the denominator on the right hand side can be simplified, giving
Req = 1/( (R1 + R2) / (R1R2) )
We can bring the denominator fraction on top by flipping it, giving
Req = R1R2 / ( R1 + R2 )
So with two resistors in parallel, the equivalent resistance is the product over the sum. Easy to remember! Just remember, that only works for two resistors in parallel. Another special case of this is the case of two resistors of the same value in parallel. Notice that in that case, when you apply the same value for R1 and R2 in the formula above, Req is half of the value of either one of the resistors. So if you have two identical resistors of value X in parallel, the equivalent resistance is 0.5X.
Test Your Understanding
view quiz statisticsAn Example Circuit
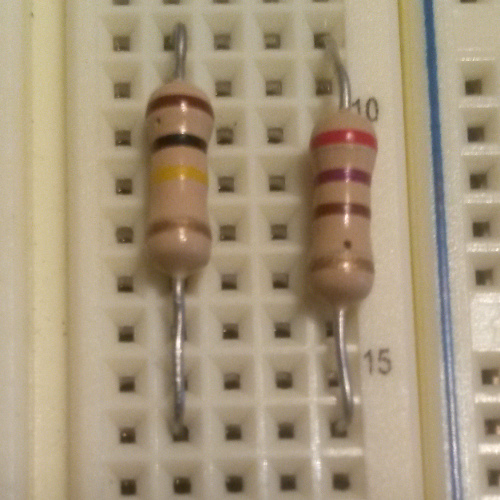
Shown below is an implementation of the schematic above on a prototyping board. The nominal/calculated values and actually measured values of different parts of the circuit are indicated in the table that follows.
Some notes:
- Parallel components have the same voltage across them, so VR1, VR2, and VR3 all share the voltage V, which is the battery voltage.
- IT is the total current that flows out of the positive terminal of the battery before it branches down any resistor path, and IRx is the current in the branch with resistor x. Notice how the three branch currents add up to the total current, just like how in a series circuit, the resistor voltages add up to the total voltage.
- To measure the actual values of each of the individual resistors, I had to remove them from the prototyping board because if I had left them plugged in and took the measurement, though it looked to me like I was placing the multimeter leads only on that resistor, there would still be an electrical path through the other resistors, and I would always get the total parallel resistance value.
- To measure IT, I pulled the red lead coming from the battery to the top node of my circuit, connected one of the leads of my multimeter in current measuring mode to it, and connected the other lead of my multimeter where the red wire originally went in.
- To measure an individual branch current, I pulled the top lead of the resistor from the top node, inserted one of the leads of my multimeter in current measuring mode where the resistor lead originally was, and connected the other lead of my multimeter to the top lead of the resistor.

Element
| Nominal/Calculated Value
| Measured Value
|
|---|---|---|
V
| 1.5 V
| 1.41 V
|
R1
| 1.2 kΩ
| 1.176 kΩ
|
R2
| 100 kΩ
| 98.7 kΩ
|
R3
| 270 Ω
| 266 Ω
|
Req
| 220 Ω
| 217 Ω
|
IT
| 6.82 mA
| 5.79 mA
|
I1
| 1.25 mA
| 1.10 mA
|
I2
| 0.01 mA
| 0.013 mA
|
I3
| 5.56 mA
| 4.74 mA
|
Observations
Most of the measured values are within expected tolerances except for IT and IR3, which seem to be too low (using Ohm's law and the measured voltage V and resistance values RTot and R3) . I tried making those current measurements with another multimeter and got similar readings.
Could it be that there was something bad about that 270 Ω resistor such that its resistance measured OK when tested alone, but when current was running through it, its resistance increased, limiting the current flow? Remember, currents in a parallel circuit node are additive, and the amount flowing in through IT was lower than it should be by practically the same amount that IR3 was lower than it should be. It's a hypothesis.
One way to test this hypothesis is to swap out that resistor and measure IR3 and IT with another 270 Ω resistor. The odds of having two identically faulty resistors would be pretty low. Unfortunately, after doing this, I still recorded similar measurements for the branch and total currents.
Have any ideas what the source of the large discrepancies between the expected and measured currents? Please leave a comment! In the next Hub, we'll look at more complex circuits with series and parallel parts. Thanks for reading!