Beginning Algebra Tutorial I--Exponents and PEMDAS

About Me
Hello and Welcome!!! My name is Patty. I am 37 years old, married, mother of four wonderful children, and recently awarded my Associates Degree in Computer Science.
While working towards my degree, Algebra was one of the hardest subjects for many students. In this tutorial, I will cover a brief introduction to some of the very basic rules of Exponents and the Order of Operations (PEMDAS).
I hope this tutorial serves as a review or helps those just learning this material for the first time. In the near future, I do plan on adding more advanced tutorials.

Lesson One---Exponents
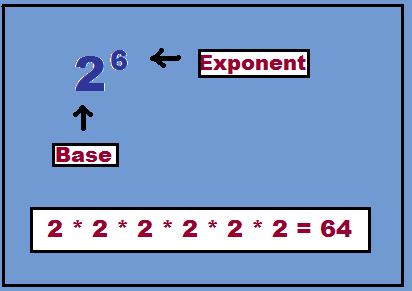
*Note that this symbol • is often used as the multiplication symbol.
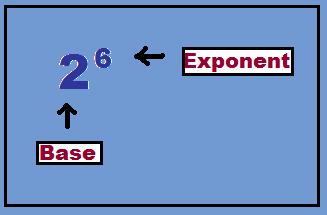
Exponents can seem intimidating to some. Exponents are used for repeated multiplication. For Example instead of saying 2 • 2 • 2 • 2 • 2 • 2, the shorter way would be to use exponents in this case 26 or "two to the sixth power".
In the example above the 2 is the base number and the 6 is the exponent.
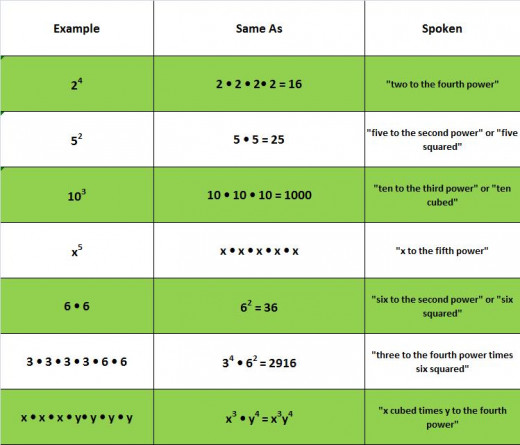
Another way exponents are shown is using this symbol ^ to show the base raised to a certain power.
Examples:
- 102 would look like 10 ^ 2.
- x5 would look like x ^ 5
Below is just some of the very basic rules which will be covered below.
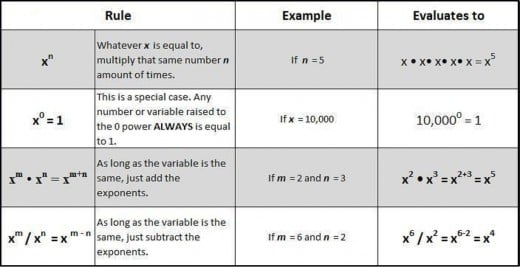
In the chart below, the variable x is the base and n and m are exponents.

Very Basic Exponent Rules

Exponent Rules Example One
xn Whatever x is equal to, multiply that same number n amount of times.

Exponent Rules Example Two
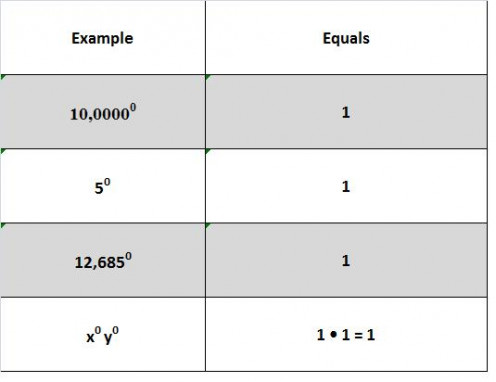
x0 = 1 Any base raised to the 0 power is ALWAYS equal to 1.

Exponent Rules Example Three
xm • xn = xm + n As long as the variable is the same just add the exponents.
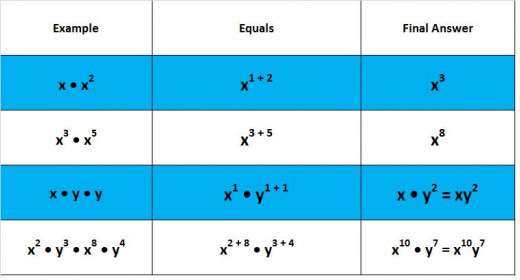

Exponent Rules Example Four
xm / xn = xm - n As long as the variable is the same just subtract the exponents.
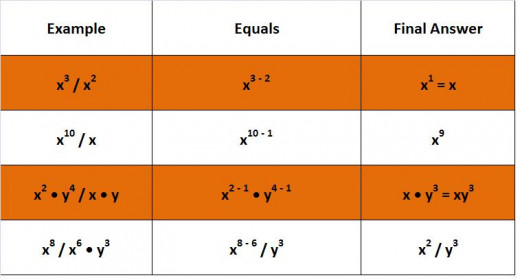


Lesson Two--PEMDAS
Lets begin with the Order of Operations. When solving an equation or simplifying an expression, solve/simplify in this order:
- Parenthesis (first solve what is in the parenthesis and/or brackets)
- Exponents (then evaluate the exponents ex. 23 = 2 x 2 x 2 = 8)
- Multiply and/or Divide (from left to right)
- Add and/or Subtract (from left to right)
One way I was taught to remember this rule:
"Please Excuse My Dear Aunt Sally!"

PEMDAS Examples
In the examples below, I will attempt to show you how to solve the problems step-by-step.

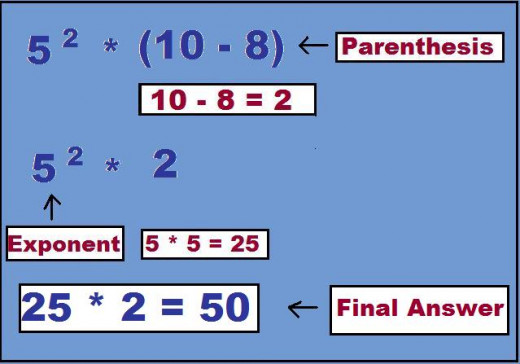
Problem 1: 5 ^ 2 • (10-8)
52 • (10-8) = ?
- First solve what is in the Parenthesis (10-8) = 2
- Now we have 52 • 2 = ?
- Then Evaluate the Exponent 52 = 5 • 5 = 25
- Now we have 25 • 2 = ?
- Finally Multiply and solve: 25 • 2 = 50

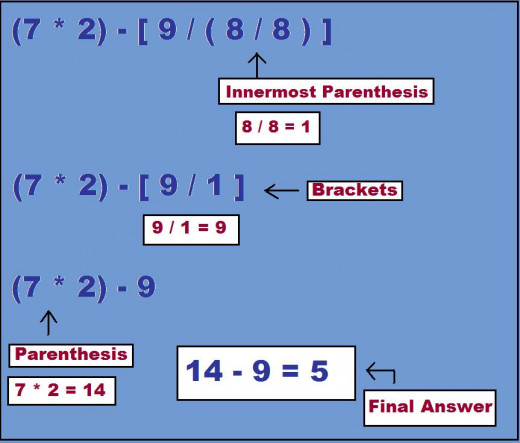
Problem 2: (7 • 2) - [ 9 ÷ (8 ÷ 8) ]
(7 • 2) - [ 9 ÷ (8 ÷ 8) ] = ?
At first glance this problem may seem tricky. In this example, we work with the innermost parenthesis, the parenthesis inside the brackets.
- First solve what is in the innermost Parenthesis (8 ÷ 8) = 1
- Now we have (7 • 2) - [ 9 ÷ 1] = ?
- Then solve what is in the Brackets [ 9 ÷ 1] = 9
- Now we have (7 • 2) - 9 = ?
- Then solve what is in the Parenthesis (7 • 2) = 14
- Now we have 14 - 9 = ?
- Finally Subtract and solve: 14 - 9 = 5

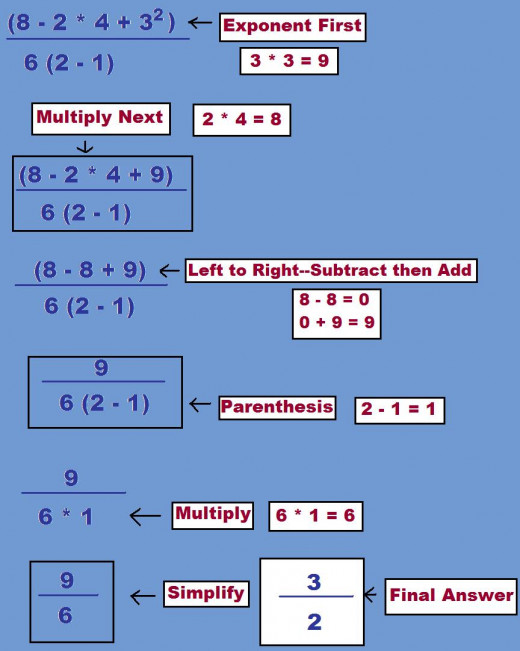
Problem 3: (8 - 2 * 4 + 3 ^ 2) / 6 ( 2 - 1)
(8 - 2 • 4 + 32 )-------------- = ? 6(2 - 1)
This problem may seem a little overwhelming at first. With this type of problem, the fraction bar acts as a type of Parenthesis. We will start with simplifying the top and then the bottom.
- On the top we will start with the Exponent 32 = 3 • 3 = 9
- On the top we now have 8 - 2 • 4 + 9 = ?
- Now the Exponent is gone we move to Multiplication 2 • 4 = 8
- On the top we now have 8 - 8 + 9 = ?
- Reading from left to right we are left with Subtraction and Addition 8 - 8 = 0
- Now on the top we have 0 + 9 = 9
- On the top we are left with 9
- On the bottom we have 6 ( 2 - 1) = ?
- First solve what is in the Parenthesis (2 - 1) = 1
- On the bottom we now have 6 ( 1 ) = 6 • 1 = 6 *Note the Parenthesis act as a multiplication symbol.
- On the bottom we are left with 6
- Now we combine the top and the bottom 9 / 6
- Simplify the fraction and the final answer is 3 / 2

Test Yourself
view quiz statisticsFinal Thoughts
I hope that this tutorial gave you a very basic understanding of the basic rules of Exponents as well as the Order of Operations, PEMDAS.
Take the test on the right to test what you have learned!! If you scored low at first...try, try again. Re-read this article, follow along with the samples provided and try the test again.
For those just learning, remember Math can be hard when first learned, but with practice and determination...Anything is possible!!!
Thank-you for taking the time to read this article. GOOD LUCK and NEVER GIVE UP!!!
If you like this tutorial, you may want to check out my next tutorial on Beginning Algebra Tutorial II--Evaluating Expressions and Solving Equations.