Beginning Algebra Tutorial II--Evaluating Expressions and Solving Equations



Welcome
My first tutorial, Beginning Algebra Tutorial I--Exponents and PEMDAS covered the very basics of Exponents and the Order of Operations (PEMDAS).
In this tutorial, I will explain how to evaluate very basic expressions and solve very basic equations.
Algebra can be difficult for many people and I hope my tutorials shed a light to those that are learning for the first time or serve to help those that have not used Algebra in a long time.

Expression Vs. Equations--What's the difference?
Equations
An Equation does
contain the = sign.
A few examples of equations:
- 5x + 2 = 32
- x/28 = 7
- 8x = 64
Expressions
An Expression does not
contain the = sign.
A few examples of expressions:
- x + y
- 2x
- 5/y

Evaluating Expressions
Let's begin with evaluating expressions. Expressions involve mathematical operations on a combination of numbers and variables. Common variables are x, y, and z, as well as a, b, and c, but many different letters are used to represent a variable depending on the problem.
When asked to evaluate an expression you simply replace x or other variables with the new value/values given.

Evaluate: 2x
If x = 5
- First, understand the problem.
- 2x means 2(x) or 2 • x
- Next look at the information we are given if x = 5
- Now wherever we see an x we simply replace x with the number 5.
- We now have 2(5) or 2 • 5
- Now solve 2 • 5 = 10
In this problem we know if x = 5 the expression evaluates to 10.


Evaluate: 3y + x
If y = 2 and x = 10
- First, understand the problem.
- 3y means 3(y) or 3 • y
- Wherever we see a y we replace y with the number 2.
- We now have 3(2) + x.
- Wherever we see a x we replace x with the number 10.
- We now have 3(2) + 10.
- 3 • 2 = 6
- Now solve 6 + 10 = 16.
In this problem we know if y = 2 and x = 10 the expression evaluates to 16.


Evaluate: 30/y + 2x + 10
If y = 5 and x = 4
- First, understand the problem.
- Wherever we see a y we replace y with the number 5.
- We now have 30/5 + 2x + 10.
- 30/5 = 6
- We now have 6 + 2x + 10.
- Wherever we see a x we replace x with the number 4.
- 2(4) = 2 * 4 = 8.
- We now have 6 + 8 + 10
- Now solve 6 + 8 + 10 = 24.


Evaluate: 96/x - 12y - 3
If x = 12 and y = 4
- First, understand the problem.
- Wherever we see a x we replace x with the number 12.
- We now have 96/12 - 12y - 3.
- 96/12 = 8.
- We now have 8 - 12y - 3.
- Wherever we see a y we replace y with the number 4.
- 12(4) = 12 * 4 = 48.
- We now have 8 - 48 - 3
- Now solve 8 - 48 - 3 = - 43


Solving Equations
Many people can solve simple math problems involving numbers, however once variables are added into the mix, some are baffled.
Properties of Equality
These properties allow us to manipulate equations to help us solve.
The same number can be added, subtracted, multiplied, or divided on each side.
What is done to one side of the equation has to be done on the other side of the equation.
Addition
- a = b then a + c = b + c Addition property c is added to both sides.
Subtraction
- a = b then a - c = b - c Subtraction property c is subtracted from both sides.
Multiplication
- a = b then a * c = b * c Multiplication property c is multiplied on both sides.
Division
- a = b then a/c = b/c Division property c is divided on both sides.
Simple Example
I will begin with a simple math problem.
We should know that 2 + 3 = 5.
Since we already know the above problem, let's throw in a variable to the same equation and solve that same problem.
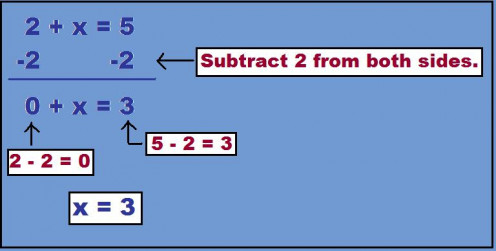
2 + x = 5
Due to the Properties of Equality we are able to manipulate the equation to solve for x.
To solve the equation we want to have the variable x by itself.
In order to have x by itself, we need to subtract the number 2 from both sides because what we do to one side of the equation we need to do to the other side of the equation.
- 2 + x = 5
- Subtract the number 2 from both sides. 2 - 2 + x = 5 - 2
- 2 - 2 = 0
- We now have x = 5 - 2
- 5 - 2 = 3
- x = 3
Notice that 3 is the same number we replaced with the variable x. This was just a simple example to give you an idea on how to solve a very basic equation.

Problem One: 5x - 2 + 4x = 16
- First combine like terms. 5x + 4x = 9x
- Now we have 9x - 2 = 16
- We want to have the x by itself. First add 2 to both sides.
- 9x - 2 + 2 = 16 + 2
- 9x + 0 = 18
- In order to have the x by itself we will need to undo the multiplication of 9x. To undo the multiplication we will need to divide both sides by 9.
- 9x/9 = 18/9 On the left side the 9s cancel out.
- x = 2
- Simplify the right side 18/9
- x = 2



Check Work
In the above equation x = 2.
5x - 2 + 4x = 16
To check work, wherever there is an x, replace the x with the number 2.
- 5(2) - 2 + 4(2) = 16
- 5 * 2 = 10 and 4 * 2 = 8
- 10 - 2 + 8 = 16
- Simplify 10 - 2 + 8 = 16
- 8 + 8 = 16
- 16 = 16
- True 16 does equal 16. So the answer is Correct!

Problem Two: x/28 = 7
This problem is actually really simple. We need to have x by itself. All we have to do is undo the division. In order to undo the division we need to multiply 28 by both sides.



Check Work
In the above equation x = 196.
x/28 = 7
- Wherever there is an x, replace the x with 196.
- 196/28 = 7
This equation is Correct.

Problem Three: 2x - 4 = -3(x + 12)
This may seem tricky at first. Going by the Order of Operations, Parenthesis come first.
- We will use the distributive property to remove the Parenthesis.
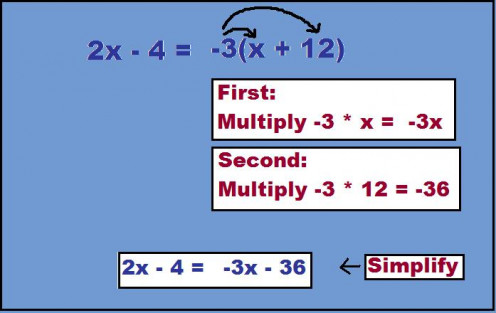
- We now have 2x - 4 = -3x - 36
- We need to have the x variables on one side. So we will add 3x to both sides.
- 2x + 3x - 4 = -3x + 3x - 36
- Combine like terms 2x + 3x = 5x and -3x +3x = 0
- We now have 5x - 4 = - 36
- We need to have x by itself so we need to add 4 to both sides.
- 5x - 4 + 4 = -36 + 4
- 5x = -32
- Divide both sides by 5. 5x/5 = -32/5
- On the left side the 5s cancel out.
- x = -32/5


Check Work
In the above equation x = - 32/5.
2x - 4 = -3(x + 12)
2x - 4 = -3x - 36 (After using the Distributive Property)
To check work, wherever there is an x replace the x with -32/5.
- 2(-32/5) - 4 = -3(-32/5) - 36
- 2(-32/5) - 4 = -84/5
- -3(-32/5) - 36 = -84/5
- -84/5 = -84/5
- True -84/5 = -84/5 so the answer is Correct.


Final Thoughts
I hope that this tutorial gave you a very basic understanding of the basic rules of Evaluating Expressions as well as Solving basic Equations.
For those just learning, remember Math can be hard when first learned, but with practice and determination...Anything is possible!!!
Thank-you for taking the time to read this article. GOOD LUCK and NEVER GIVE UP!!!