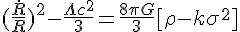
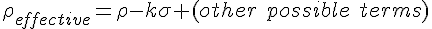
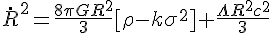
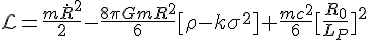
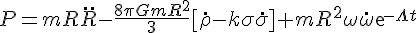
An Overview of my Work: Part Two

In this post, we are going to have a lot less talking and more equations; in my last post,we pretty much covered all the aspects I believed in so I don't wish to get into them again with too much depth. In this post, I will take you through some key equations of the investigation.

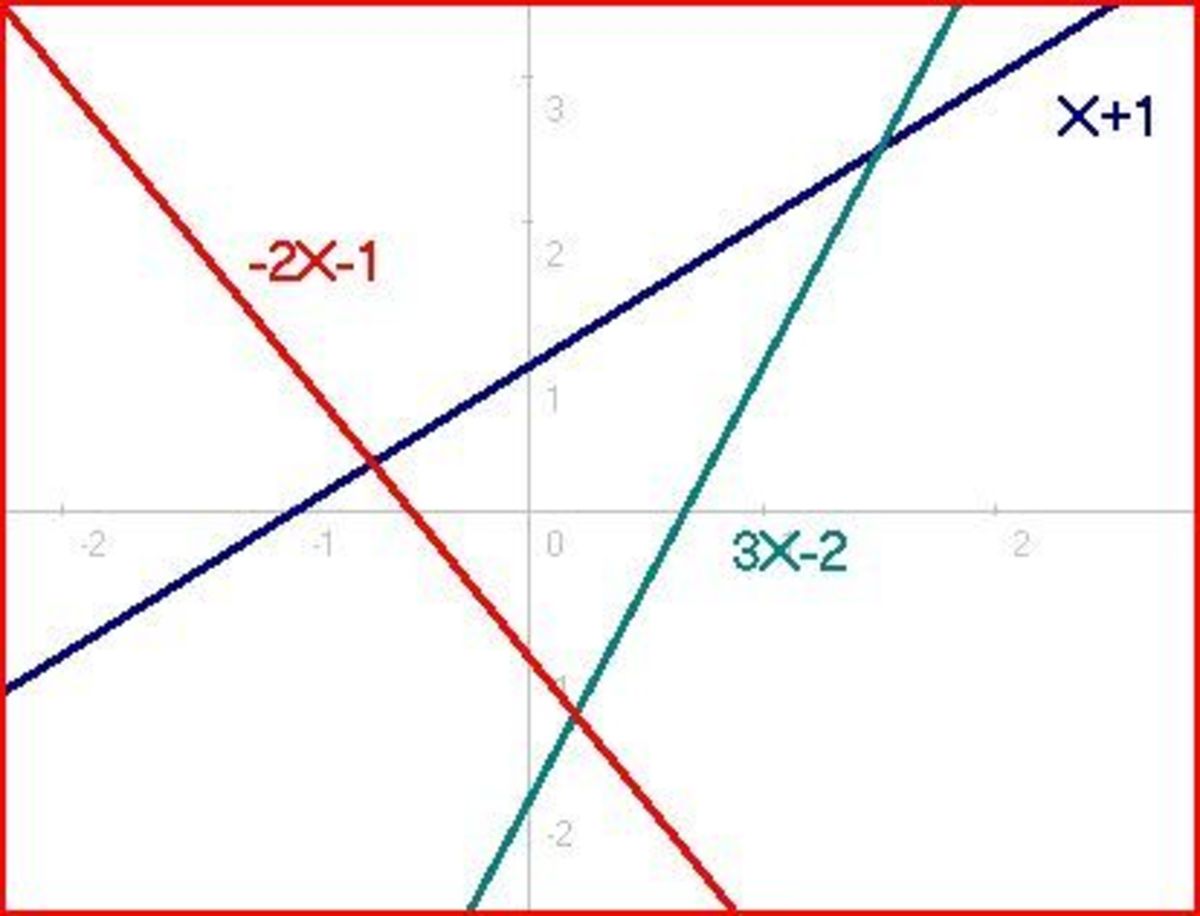
From the list of equations above, the first we take a look at the modified Friedmann equation for an evolving universe with torsion. The next equation describes the effective density part. The next equation is just rearranged for the time derivative of R squared, but doing so we get ΛR² which can be thought of as making R²/L² with L being the Planck length, which effectively scales R with the Planck length

Equation 4, is the Friedmann Lagrangian, an equation I derived myself from the field equations. And finally, the last equation is the Friedmann power equation for the universe, where the power is marked by a change in the energies associated to torsion and to the spin.

NOTE:

The Friedmann energy equation I derived can originally be given with the spin as well. But in some treatements, the rotation may be directly linked with dark energy and so may be the definition of the cosmological constant. In the equation below, the Friedmann energy equation with rotation and a cosmological constant is

E = mR'² = 8πGmR³/3R ρ - mR²ω² + (mc²/3)Λ²R²

If dark energy is rotation, then the cosmological constant can take the form of:

Λc²/3 = ω²

which has a value of

Λ = 3ω²/c² = 10^-56 cm^-2

which is the observed value. The torsion is

Q = 4πGσ/c³ = 10^-28 cm^-1

and the background curvature of the universe is approximately the square of the torsion

Q ² ≈ 10^-56 cm^-2

To get the Lagrangian, you just set the equation to zero and it becomes the Lagrangian

mR'² - 8πGmR²/3(ρ - kσ²) + mc²/3(R/L)² = 0

And the effective density part may be much bigger. A theoretical, non-conserving Friedmann equation I investigated takes the form of:

R'R'' = 8πG R²/6[ρ'(on) + ρ'(off) + ρ'(grav) + ρ'(EM) + ρ'(vel) + ρ'(spin) + ρ'(vac)]

One day I will write up about this equation here as well.