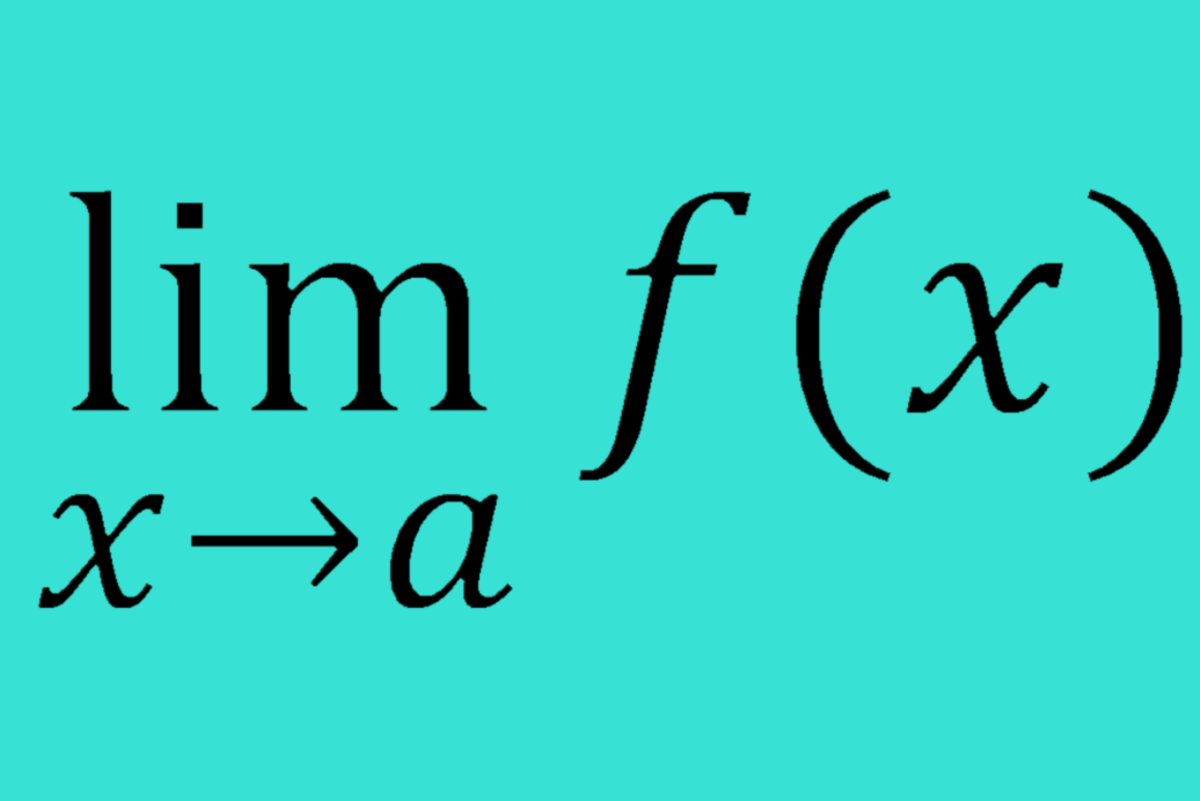Calculus demystified Part 3

We wonder, what in the world! was Issac Newton thinking?

NEWTON

"Sir Lord...If you know me by know, it was the right approach from my own thinking"

LORD

We just found out that you have some type of Aspergers, My 'Sir Newton'

NEWTON

I don't understand you at all!, even your accent is different Sir Lord. Asperberger? Who is that?

LORD

Sorry! Never mind..! We want to get your approval in demystifying this matter, once and for all, My Lord Isaac...!

NEWTON

From our optical point of view and if the celestial bodies approve...alas! We will see, Sir Lord!

BASICS OF INTEGRATION

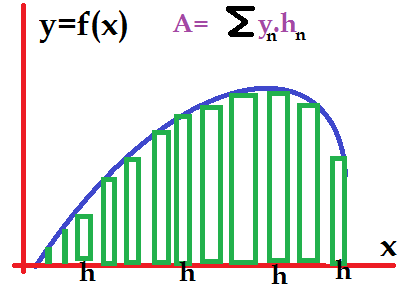
Imagine you have to fence up your backyard with pieces of wood. The catch is that you have to make them fit on the curve shown on the graph(in blue). You know that every piece of wood(vertical slabs) has an individual area of

A₁=Y₁ H₁

Now, common sense tells you that the total area of that fence will be obtained adding the individual areas which will be represented by the summatory on the graph. But, the problem is, you really didn't cover the whole area smoothly for the curve F(X)=Y. That's where our Math wizards from Mesopotamia, and Egypt, and seventeenth century Europe forefathers tried to solve. Enter Integration '∫'...Now off the record, we suspect that Leibniz created the symbol for integration by accident, since Latin was in vogue. Newton did win on this election of the ∫ symbol for Integration; Could've been I as in integrals, but we can tell you Sir Newton, that if you mend the two first letters of your name, you will see what we are talking about. "I'm certainly impressed Sir Lord. Sleek and clever!"

INTEGRATION

We want you to know... that from now on, the inverse of integration is called differentiation. So we are already linking both math tools by our statement. From the graph above, lets make up to what our teachers told us: We chose an interval 'a' and 'b' for x, then if we represent f(x) as the curve in blue. We can 'integrate' the and finally reach out to the formula: But lets state it in a mathematical form:

We are given a function ƒ of a real variable x and an interval [a, b] of the real line, the definite integral. (indefinite integrals for a later hub)summatory

∫f(x)dx

is defined informally to be the net signed area of the region in the xy-plane bounded by the graph of ƒ, the x-axis, and the vertical lines x = a and x = b.

We introduced finally the main purpose of this scary representation. This reminds us of the + sign when we were seven years old, right?

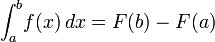
A function F whose 'derivative' is this famous f(x) is called indefinite integral and is represented by

F=∫f(x)dx

Now, take it easy on that. We want you to think...that, "dx is the one Lord told us about in Differentials," so somehow Integration and differentiation are connected, we just need to look for that dy in that tricky F.

if f is a continuous real-valued function defined on [a, b] called close interval, then, once an anti-derivative F of f is known, the definite integral of f over that interval is given by the graph up above.

RIGHT FRESH TO AN EXAMPLE:

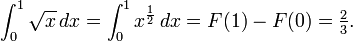
The antiderivative of x^1/2

Can be found in well known tables but for now is like this: F(x) = ²⁄₃x^3/2

We know that ∫xⁿ dx=(xⁿ⁺¹) /n+1 +C where C is a constant

We simple do the operation for intervals[0,1]

F(1)- F(0)

2/3-0=2/3

We hope we have given you some head start on this important subject for a future Engineer or a Scientist....we will continue on a Part4, where we will work on integration by parts.