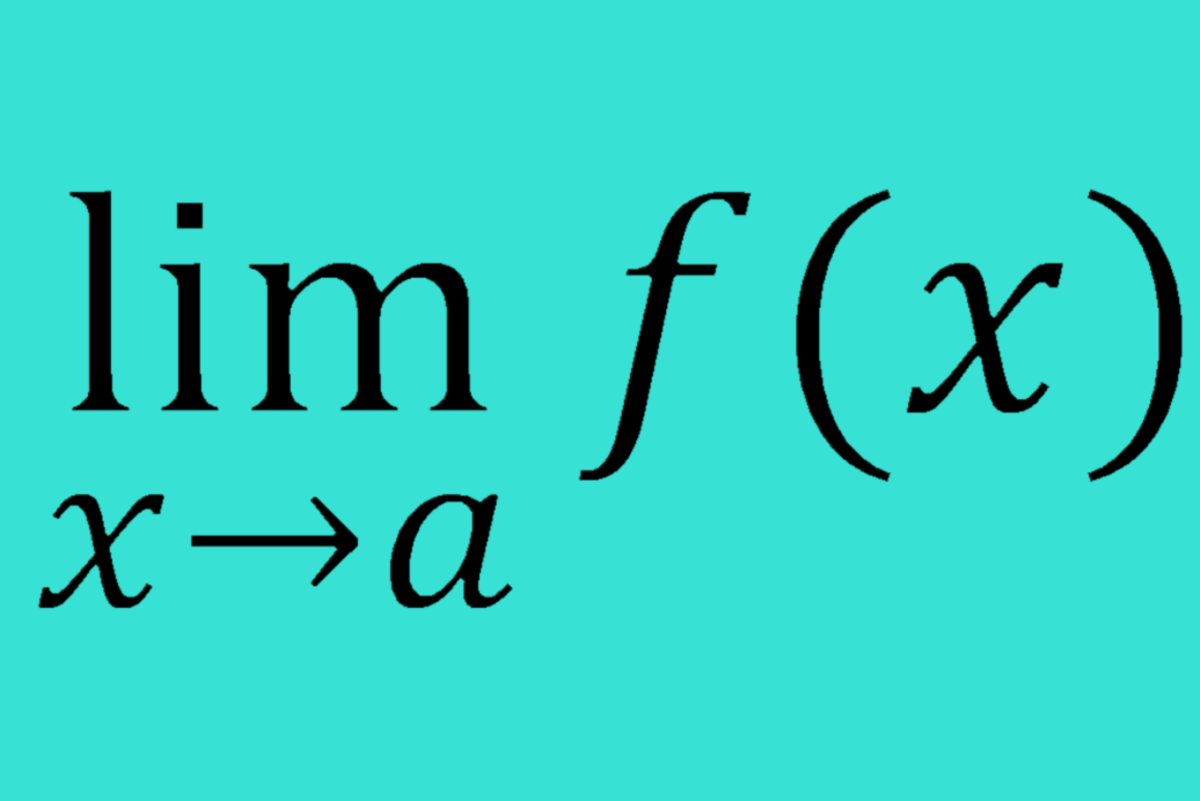Calculus demystified for Real People, Part 4 -- Formulae Rearranged

Integration By Parts

Since we started to study ourselves this crazy math..we wanted to find ways to simplify 'Heuristically' using easier Methods and our own Mnemonics instilled in us by our Tutor... That our Dad got us in Junior High. Lucky us right?

Using some rules of Calculus and rearranging formulas we can attack more complicated problems that will arise in the life of a College dude, you know?

STRAIGHT TO our Subject

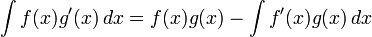
The Equation to the right has a derivative g′ that could be a handicap since we usually see more down to earth functions that multiply themselves as in f(x).g(x)

If we really need a practical formula for

∫f(x).g(x)dx

We postulate a new arrangement as in the formula below. You can obtain this new formula by Integrating both sides of the equation

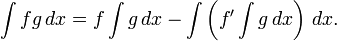
We've got to make sure that f can be differentiated to f′

and g be able to get integrated as well...

EXAMPLE :

We should know that ∫(1/x²)dx = -1/x

and ∫x^-1dx = ln/x/ +c

Consequently Inversely , we can asses that:

(ln x) ′= 1/x ( differentiation of natural logarithm for x)

Let's say we want to integrate this function....we know beforehand that we can break it down...

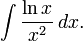
We rearrange it to our formula of 2 functions

∫(lnx)(x^-2 )dx= lnx ∫x^-2dx- ∫ f′ (∫g)dx

where f′ equals to 1/x

and g integrated (∫g) equals to -1/x

replacing in the formula for integration of two functions of the type ∫f.gdx=??

we get the easier to solve equation:

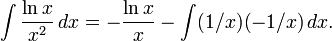
The answer is

-lnx/x -1/x

or -(lnx+1)/x

You should know by now that

∫x^k or ∫x^k = x^k+1/k+1

and inversely

(x^k)′= kx^k-1 (differentiation of a power)