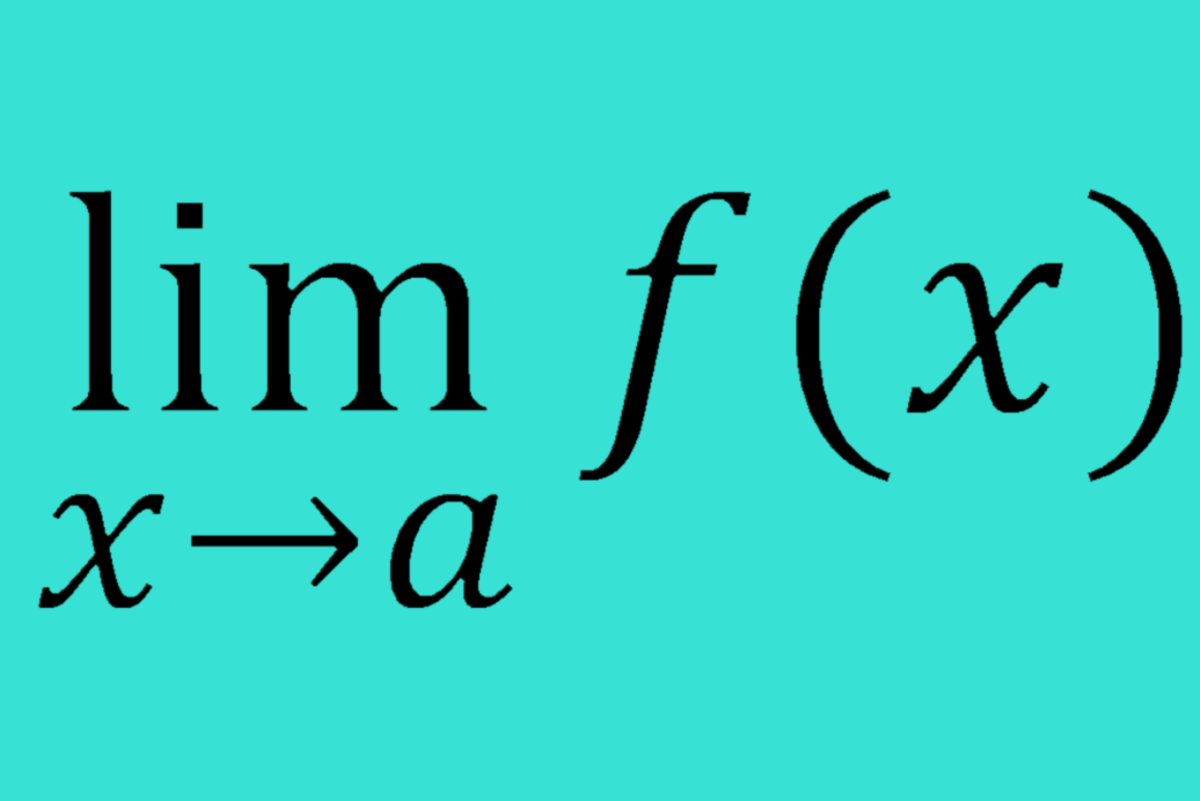Complex Logarithms; part 1: Natural log with a negative argument
2. Paragraphs 12, 13 and 14 is the continuation, from the previous hub, of God's "unconditional" love.
THE ARGUMENT OF A LOGARITHM:
3. The argument of a logarithm is the number or function next to the logarithmic operator. So in this hub it would be the number 1000 in log10(1000). Normal logarithms have positive arguments; however, complex logarithms can give you positive, negative or complex arguments. Although the arguments that complex logarithms can give, including complex numbers and complex functions, can be very diverse there has never been a documented case in the history of mathematics that a complex logarithm gave an "ad hominem" argument. Aren't we all glad of that since we had a belly full of those in elementary school, and from teenagers when told they should stop smoking.
WORK ON L1 THROUGH L7 EXPLAINED:
4. At L1 the number 1000 is the argument for that logarithmic function. A logarithmic function essentially says, What value must the base( 10 in this case) be raised to give an argument of 1000. Of course that value is 3 as shown at L2. We can convert L1 into L2 by exponentiating( a term some authors use). L3 is exponentiating L1; i.e. using L1 as an exponent for the base 10. L2 is the exponential form for L1. At L3 the laws of exponents cancel out 10 raised to the log10 which just leaves the argument of 1000. You can read L3 as 1000 = 103 = 1000. L4 is the natural log function, which has the natural base, "e". The number e is an irrational number( does not settle down to a repeating decimal or a quotient of integers). Its value to 12 decimal places is 2.718281828459. So at L4 the natural log of 153 is about 5.03, which means at L5 that e raised to the 5.03 power will give about 153 for an answer. L6 and L7 repeat the same principle as L3 and L2.
THE IMPOSSIBILITY OF HAVING A NEGATIVE ARGUMENT:
5. L8 is what this hub is about; i.e. in the field of real numbers you can not solve a logarithmic function with a negative number for the argument. L8, L9 and L10 shows why this is impossible. At L8 what number x will you raise 10 in order to get a minus 7? Raising 10 by a positive power will only give you a number from close to 1 to toward infinity depending on the power. Raising 10 to a negative power will just give you a small number from less than 1 on down to approaching zero depending on the value of the negative exponent. Therefore, there is no real number you can plug in for X at L8 to get --7( minus 7).
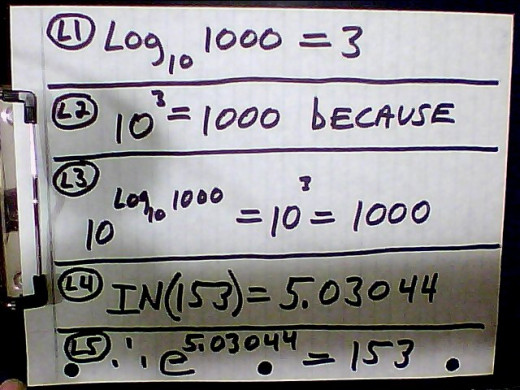
THE FIELD OF COMPLEX NUMBERS TO THE RESCUE:
6. Since mathematics is, in my opinion, God's language---because we progressively discover it, not invent it---we should have expected that taking the log of a negative number would not forever be impossible; after all "with God all things are possible"( Mathew 19:26). We poked around trying to figure out how to do this and finally, many years ago( antilog10 (2.66932) to be more accurate; date now is 2012), we discovered God's field of complex numbers and found a way it could be done. It took us into another dimension--literally--but sometimes that is what it takes to do the impossible. Yes "with God all things are possible"( Mark 10:27) but you have to follow God's rules to make that happen; therefore, we had to follow His laws of complex numbers to find the log of a negative argument.
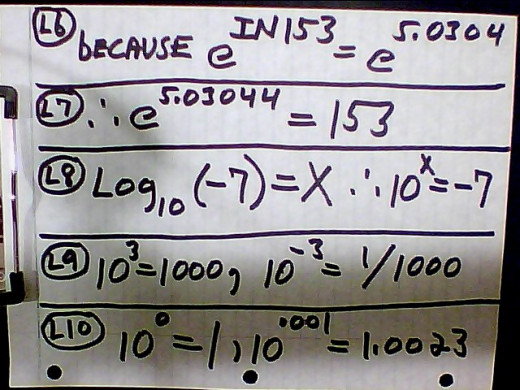
EULER'S FORMULA--HAVE STRONG COFFEE BREWING:
7. Let's take the natural log of --153 at L11, which says, as explained, e must be raised to the complex power z to give --153. L12 writes z in its rectangular, or Cartesian, coordinate form ( X + Yi). The location of X is found on the X-Axis, and Y is found on the Y-Axis; therefore, we have left the dimension of a single line( the real numbers, X), and entered a 2nd dimension of the imaginary numbers( Y), and we are now in the realm of a plane. L13 is simply following the law of exponents and rewrites the exponential function as shown. I changed Y to θ because we will be using Euler's formula( sometimes called identity or equation). Now here is where it gets tricky. At L12 Y represents the Y-coordinate, and as such is 90 degrees( or perpendicular) to the X-Axis. If you will take a look at L31 you will see the arrow of that vector stops at a point on the plane. That point represents a complex number in the plane, and the coordinates of that complex number are represented by the X and Y axes. The complex number is about 32 degrees off the x-axis and located about 6 units from the origin. The Y value at L12 does not represent the same thing as the θ value of L12. They have the same numerical value but they are representing different things. The Y number represents the imaginary component of the complex number, but the θ number represents the angle in radians being used in Euler's formula. I can get away with this because I'm converting to Euler's formula, which is derived in complex analysis, and involves infinite series. Y is pi( 3.14) imaginary units, while θ is pi radians in Euler's formula, and z, the complex number, has an angle of 0.558 radians( about 32 degrees). Math is learned by doing the math. I reread this and it is confusing. As one does problems as these, then as you are solving them the concepts become clear, and you will--as in this case--be able to understand the difference between Y and θ at L12. You have to do the problems to understand math; otherwise, nearly everything in math will seem obscure.
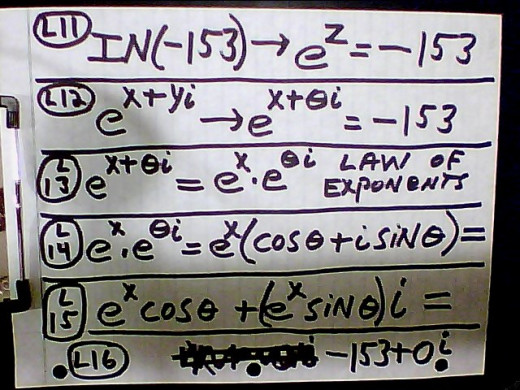
WORK ON L14, 15, AND 16 EXPLAINED:
8. L11, 12 and 13 were explained in the previous paragraph. L14 is Euler's formula. Its derivation and existence will not be explained in this hub, but as usual, we will just follow the rules of math in using it. Euler was a brilliant mathematician, and many mathematical discoveries were made by him. At L15 we just distribute eX to each of the trig functions. The i in front of sin θ tells us this is the imaginary component of the complex number represented by Euler's formula. All the real numbers are a subset of the field of complex numbers; therefore, at L16 the real number of negative 153 is written in its complex form. 0i at L16 is its imaginary component, and it makes sense, since it has a zero imaginary component, making the --153 a real number.
WORK ON L17, 18 AND 19 EXPLAINED:
9. L16 equals L15; therefore, the real component of L15, which is eXcosθ equals the real component of L16, which is --153. Similarly the imaginary component of L15, which is eXsinθ equals the imaginary component of L16, which is zero. This is all represented at L17. We need to solve for θ and X via the simultaneous equations of L15. We want to use a trigonometric identity( trig ID) to get rid of sinθ, and we do this by squaring both equations at L18. The trig ID is substituted for sin2θ at L19
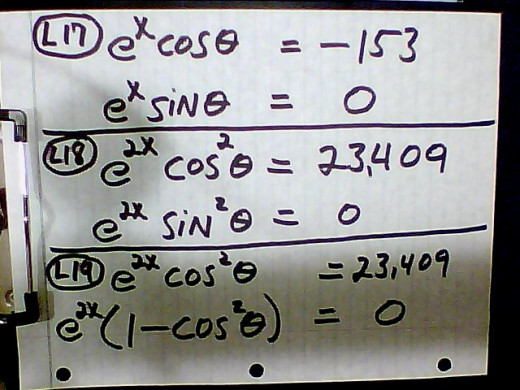
SOLVING FOR X AT L20 THROUGH 23:
10. We add the simultaneous equations at L20 and end up with an equation with only one variable to solve. If that variable is an exponent or part of an exponent then logs are the best way to solve it. Since L20 is an exponential equation to the base e, then taking the natural log of both sides of the equation is the way to go at L21. Laws of logs puts the 2X in front at L22, and IN(e) cancels out to one. The 1.006088 at L22 is supposed to be 10.06088. Finally the X is isolated at L23 and solved to be 5.03044.
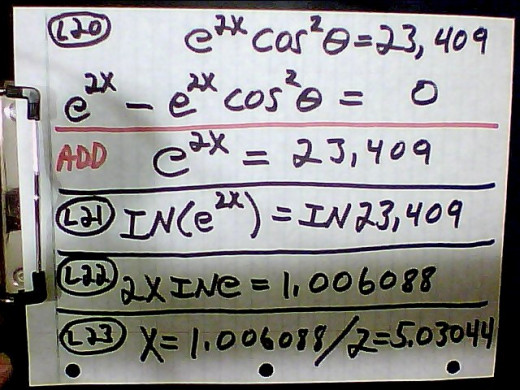
SOLVING FOR θ AT L24 THROUGH L27:
11. This value of X is plugged into the first equation of L17, and this is done at L24. We take the arc cosine of both sides of the equation at L26 in order to isolate θ, and we get a value of pi radians. We have determined both X and Y of the complex number Z and their values are placed at L28. This complex number is put into a form that we can give a graphical representation of it as a vector at L29 through L31. So our answer for this problem is
e(5.03044 +3.141593 i) = --153; therefore
In(--153) = 5.03044 + 3.141593 i
which was the problem we started with at L11.


BOILED ALIVE AND LOVING EVERY SECOND OF IT:
12. This subject of God's "unconditional" love is continued from paragraph 12 of hub#12.7 ( trig to algebraic). The previous paragraphs on this subject may imply that if a Christian sins then--bam--he/she is going to hell. It is not my intention to leave that impression; however, I do believe we are making assumptions concerning God's tolerance that can lead us to eternal torment, and we make assumptions concerning our vulnerability when we allow sin to reign in our lives. When I think of sin and our lives, I think of a story given by a motivational speaker. He applied the story to how we settle into a complacent and mediocre life; thereby giving up on our hopes, dreams, ambitions and aspirations. I think it can also be applied to our sin, conscience, rationality, and eternal fate: If a frog is thrown into boiling hot water he will jump out immediately. Put the frog in water at a comfortable temperature, and he will be content. Then if the temperature is slowly turned up, that frog can be boiled alive; he will not jump out. He will acclimate to the increasing temperature, and remain content. Eventually he dies, but his death began when he remained in the water.
SIN, SOPHISTRY AND SENSE:
13. Sophistry is a powerful word because it is so prevalent in society, as for example politics, but its greatest power is in feigned christianity. When used by politicians it can allure and deliver an entire nation into tyranny; however, that is not possible until it does its pernicious work with the lukewarm christianity within a nation( Leviticus 26:3--6 with 14--17; Jeremiah 18:7--10; Ezekiel 39:23--24). Sophistry is argumentation that has a ring of truth, but is still fallacious. As explained at paragraph 3 of "Intention of Demons," sophistry weakens faith. It rationalizes sin, and sin opens the door for more deception( 2 Timothy 3:13; Jeremiah 9:6; Isaiah 44:20; James 1:26( a major sin leading to an inundation of deception)). Faith adheres to John 7:17 and expects to be delivered from deception. Sophistry ignores the Scripture that says sin is of the Devil( 1 John 3:8; John 8:44 with 47), but faith will acknowledge it. An example of sophistry is, "We are saved by faith and faith alone. It is the gift of God; you can not work your way into heaven." The Scripture to back that statement up is Ephesians 2:5 and 8, which is absolutely true, but the statement is used to imply we can continue to sin, and still be saved. This sophistry will ignore James 2:17, 20 and 26, or Mathew 3:10; and 7:17--19; 1 John 2:3-5, and oh! so much more. If you are a Christian, then does it make sense to you that God would give us hundreds of verses concerning obedience, and yet not expect us to obey them. Does it make sense that God gives us numerous warnings concerning disobedience, and yet not follow through with those warnings?
PAUL SAID, "I HAVE FOUGHT A GOOD FIGHT "( 2 TIMOTHY 4:7):
14. As I said at paragraph 12, I do not want to leave an impression that a Christian sins and immediately is going to hell. These arguments are focused on those of us who are comfortable in the boiling water of paragraph 12. They are focused on how pernicious and precarious it is to toy and play around with sin. I do believe that there are numerous people who believe they are saved but are not saved because the boiling water is just so comfortable, and even if one keeps jumping out because of conscience, it is just so much fun jumping back in again. In Voice CIW's hub he gives an encouraging perspective on this subject. I agree with most of what he wrote; nevertheless, I do, at this time, believe one can sin to the point of losing his/her salvation. When I make the argument to confirm that believe we'll see if I change my mind, but that will be for later. I think Paul's attitude is one all Christians need to secure as their own: FIGHT, FIGHT, FIGHT against sin to the point you hate everything about it. With God all things are possible. Another way to fight is to have the right perspective of God, which North Wind describes in her hub, Is God Your Master or Your Slave?