Differential Calculus
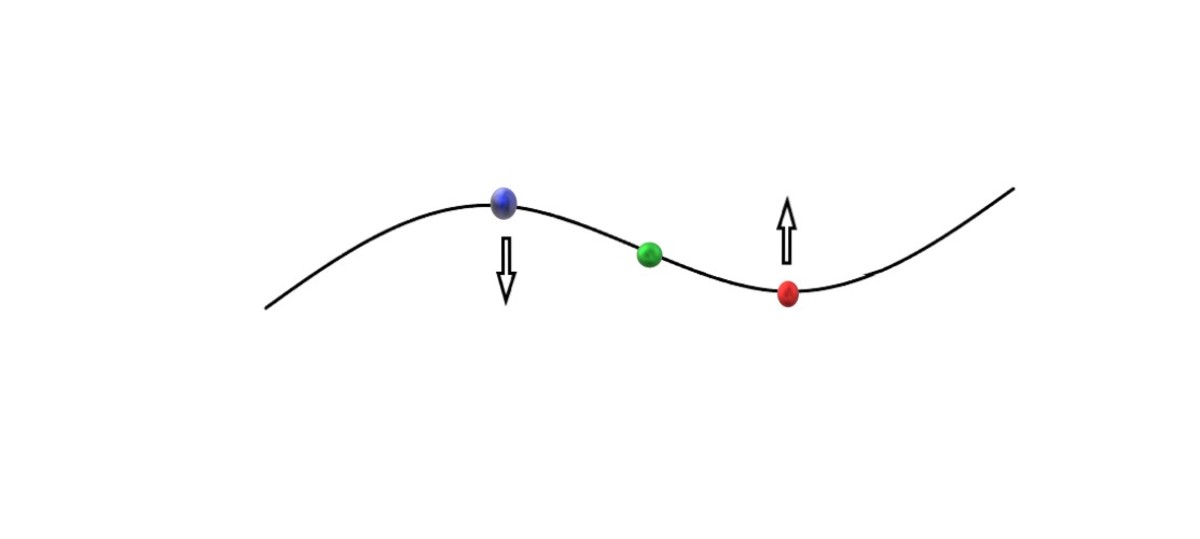
Differential calculus is simply the process of finding the gradient of a curve at any point. That may not sound very exciting, but what is fascinating is how many applications calculus has. Calculus is widely used in physics, astronomy, engineering and economics.
To see a fun example of how calculus is used in astronomy, by using calculus to work out the amount of fuel to place on board a rocket, read this article:
How Calculus is Used in Astronomy
Calculus is used in any problem where something is changing or moving, and you need to find the rate at which that change occurs. It's also useful for finding maximum points, or optimal solutions. To find out how to use differential calculus to calculate the maximum or minimum point of a parabola, please read:
Principle of Differential Calculus
To find the gradient of a straight line, as every high school student learns, you need to divide the change in y between two points on the line by the change in x between the two points.
∆(y) / ∆(x) = gradient
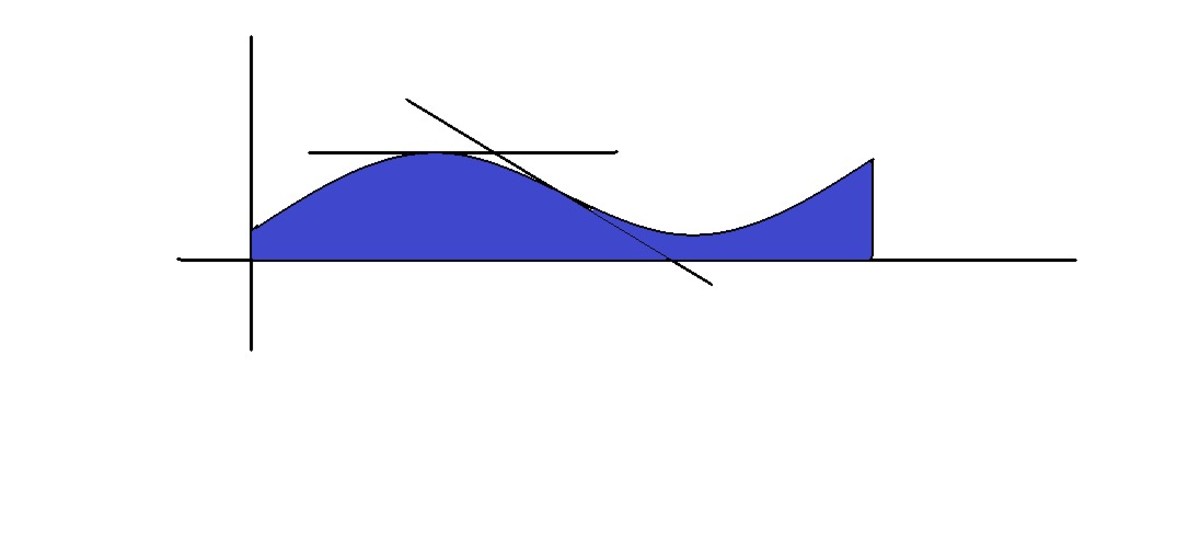
A curve can be approximated by a series of straight lines that connect two points on the curve. Working out the gradient of each straight line gives an approximation of how the gradient of the curve varies. The closer together the two points on the curve are, the more accurate the calculation of the gradient will be.
δ(y) / δ(x) ≈ gradient at (x,y)
Here we have used a small delta “δ”, instead of a capital delta “∆”, to indicate that the changes in x and y are very small.
A completely accurate answer to the gradient of the curve is obtained using a tangent of the curve. To find the tangent to the curve, we move the two connected points on the curve closer and closer together until they are both at the same point.
To represent this mathematically, we make our changes in x and y smaller still, like we did when we reduced them from ∆(x) and ∆(y) to δ(x) and δ(y). Now we make them into infinitely small changes, which we represent by dx and dy.
dy/dx = gradient at (x,y)
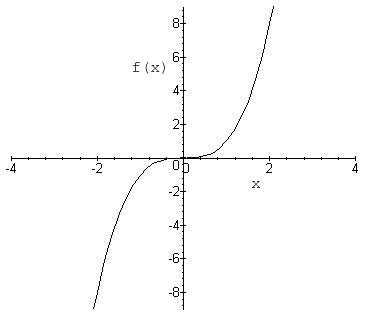
Example: the cubic
As an example, let's calculate the gradient of the curve y = x3 at the point x=2, y=8.
First (poor) approximation:
Approximate the curve as a straight line between x=1.5 and x=2.5
Coordinates of point one: x = 1.5; y = 1.53 = 3.375
Coordinates of point two: x = 2.5; y = 2.53 = 15.625
Gradient ~ (15.625-3.375)/(2.5-1.5) = 12.25
Second (better) approximation:
Approximate the curve as a straight line between x=1.9 and x=2.1
Coordinates of point one: x = 1.9; y = 1.93 = 6.859
Coordinates of point two: x = 2.1; y = 2.13 = 9.261
Gradient ≈ (9.261-6.859)/(2.1-1.9) = 12.01
Using calculus to calculate the gradient (completely accurate)
Let y = x3. Take two points that are infinitely close together to calculate the gradient.
Coordinates of point one: x = x; y = x3.
Coordinates of point two: x = x + dx; y =(x+dx)3 = x3 + 3x2dx + 3xdx2 + dx3
Because “dx” is infinitely small, dx2 ≈ 0 and dx3 ≈ 0
Gradient = (3x2 dx) / dx = 3x2
The gradient of the curve y = x3 at (x,y) is 3x2
For the point x = 2, y = 8, the gradient dy/dx = 3(22) = 12
So our first approximation, 12.25, was quite inaccurate. Our second approximation, using a smaller section of curve, was better, at 12.01.
Quick Reference
y = xn --------------> dy/dx = nxn-1
y = constant ------> dy/dx = 0
y = ex ---------------> dy/dx = ex
y = ln(x) ------------> dy/dx = 1/x
y = sin(x) -----------> dy/dx = cos(x)
y = cos(x) ----------> dy/dx = -sin(x)
Rules of Differentiation
You can repeat the process we just went through to calculate the gradient of any curve, for example:
y = ax2 + bx + c
y = √x
y = ex
By calculating the gradient for all of these curves, you should begin to realise that there are rules for differentiating different types of functions.
Any term in the function that has the form xn differentiates to nxn-1. This works for any value of n, including fractions and negative numbers.
The exponential function, ex, has the special property that it differentiates to itself.
The number e is defined to give this property. It has an approximate value of 2.71828183... Like pi, it is an irrational number: if you write it down as a decimal, it has an infinite number of digits.
Resources

Uses of Calculus
- Calculus and Astronomy: How do they Relate?
Calculus, the mathematical study of variations, is as widely used in astronomy as it is in all other areas of physics. It is used to describe the motions of planets, spaceships and other astronomical bodies. - How to find the Vertex of a Parabola
A parabola is a curve which is given by a quadratic equation: y = ax2 + bx + c Every parabola contains a vertex. A vertex is the maximum or minimum point on the curve, at which the gradient of the curve is...