Does Motion Affect The Speed At Which Time Passes? (Part 4 of 4)

Before we proceed, let’s take a quick timeout to summarize the mind-numbing discoveries that we have thus far gleaned from Albert Einstein’s special theory of relativity, starting with his fundamental postulates and then carrying through to the time dilation and distance contraction phenomena.

• The first postulate, also known as the principle of relativity, asserts that observers in a system which is moving in a straight line and at a constant speed – that is to say, moving with uniform, or non-accelerated motion – cannot feel or sense this motion. In fact, the observers have every right to claim that they are the ones who are at rest and it is the outside world that is moving instead, because all of the laws of physics will operate in exactly the same manner for the observers as they will for those in the outside world. Therefore, there is no experiment that the observers can perform, in the whole of the physical universe, that will detect or reveal whether they are in uniform motion or at rest. The two situations are equivalent.
• The second postulate asserts the invariance of the speed of light. In other words, it asserts that observers in relative uniform motion, regardless of what the relative speeds between them may be, will always measure the speed of light, using their respective rulers and clocks, to have the constant, unchanging value of 186,000 miles per second, or 669,600,000 miles per hour! This is indeed extremely bitter medicine to swallow (to say the least), because it goes against every grain of logic and common sense that we hold about the very intuitive concept of adding and subtracting relative speeds. But it is the correct medicine to ingest nonetheless, as the invariance of the speed of light has been confirmed by countless experiments, the most famous being that performed by Albert Michelson and Edward Morley in 1887.

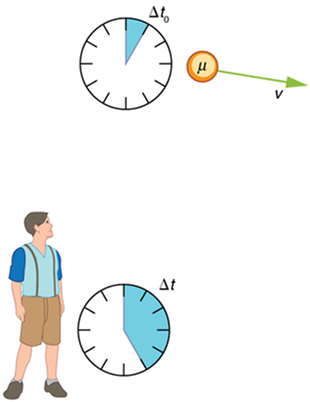
• The time dilation phenomenon arises as an unequivocal consequence of the reality of special relativity’s two fundamental postulates, as we have discovered from our previous thought experiment concerning the photon clock aboard Scotty’s train. Due directly to the second postulate, Scotty’s relatively moving photon clock ticks at a slower rate than our relatively stationary photon clock, as observed from our point of view. This is the case, because Scotty’s photon has to travel a longer distance to complete one tick than our photon does to do the same, and since his photon and our photon must both travel at the same speed of light c, it will thus take Scotty’s photon a greater amount of time to complete one tick than it takes our photon to complete one tick, as observed from our point of view. And since greater relative speeds mean longer and longer distances for Scotty’s photon to travel in order to complete one tick, then the greater the relative speed, the slower the (relatively) moving photon clock ticks. Now, however, due directly to the first postulate, we must and will observe all timekeeping devices, all physical processes, and indeed, time itself aboard Scotty’s train, slow down by the same amount that his photon clock has slowed down! If this was not the case, then Scotty could use the loss in synchronization between his photon clock and all of the physical processes aboard his train to deduce that he was the one that was truly, absolutely moving, which is a deduction that the first postulate asserts cannot be made! Thus, time slows down for objects that are in relative uniform motion! And just as greater relative speeds mean slower and slower ticking clocks, it therefore follows from the first postulate that greater relative speeds mean that time itself passes by more and more slowly!

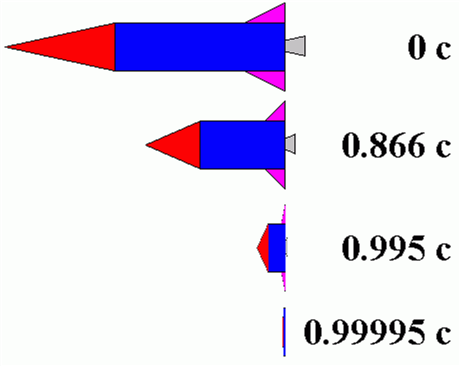
• As the furious flight of the cosmic muons has demonstrated, the distance contraction phenomenon (along the direction of relative motion), is an unequivocal consequence of the time dilation phenomenon. Muons, on average, live a very short life of only 2.2 x 10^-6 seconds before they disintegrate. We still observe, however, that, travelling at a speed of 0.998c relative to the earth, these muons are able to traverse the full height of our atmosphere and penetrate well beneath the earth’s surface, a journey that spans a distance of 34,184 feet, as measured by our rulers, and that takes a much longer 34.8 x 10^-6 seconds of normal time, as measured by our clocks! Hence, as observed from our point of view, it is the time dilation phenomenon that allows the muons to accomplish this feat without disintegrating before even coming close to the earth’s surface. Since the relative speed between the earth and the muons is 0.998c, we observe that the passage of time for the muons is slowed down by a (time dilation) factor of 15.82. THUS, we observe their 2.2 x 10^-6 second lifespan to be dilated, or stretched out, over the course of (2.2 x 10^-6 seconds) x (15.82), or 34.8 x 10^-6 seconds of our normal time, which is enough duration for them to penetrate well beneath the earth’s surface! As observed from the muon’s point of view, however, it is the distance contraction phenomenon that allows the earth – which is, of course, travelling at a speed of 0.998c relative to the muon – to slam into it, BECAUSE from the muon’s perspective, time is passing by at the normal rate, and so its internal clock is not running slowly at all. AND SINCE the equation for distance travelled is { DISTANCE TRAVELLED = SPEED OF TRAVEL x TRAVEL TIME }, THEN, after a normal 2.2 x 10^-6 seconds of lifespan have elapsed on its internal clock, the muon MUST find itself already buried well beneath the earth’s surface as it disintegrates, after the earth has travelled a distance of only (0.998c) x (2.2 x 10^-6 seconds) = (9.823 x 10⁸ feet/second) x (2.2 x 10^-6 seconds), or only 2,161 feet towards it, as measured by the muon’s rulers! THEREFORE, from the muon’s perspective, the entire 34,184 feet of travel distance that we have measured must be contracted, or compressed, into the 2,161 feet of travel distance that the muon has measured! HENCE, the time dilation that we observe happening to the muon results directly in the muon “seeing” a contracted travel distance, and therefore, distance contraction along the direction of relative motion is a direct result of time dilation. Moreover, the greater the relative speed between the earth and the muon becomes, then the disproportionately less will be the amount of time that we observe to elapse on the muon’s internal clock during its journey, because of the greater and greater, ever present effect of the time dilation phenomenon. And therefore, upon further examination of the above equation for DISTANCE TRAVELLED, we realize that even though the SPEED OF TRAVEL will indeed be greater, this greater speed will clearly not be able to offset any of the lesser TRAVEL TIME that we will observe to elapse on the muon’s internal clock due to time dilation. Therefore, the greater the relative speed, the shorter and shorter distances become!
• Time dilation and distance contraction are both symmetrical phenomena, as far as relative uniform motion (i.e., motion in a straight line and at a constant speed) between any two given observers is concerned, because each observer, by the first postulate, has every right to claim that they are at rest and it is the other that is moving. HENCE, each observer will claim that the other’s clocks are ticking more slowly than theirs, while their clocks tick at the normal rate of time passage, and each observer will claim that the other’s rulers are shorter than theirs, while their rulers are at their normal lengths! Therefore, as long as the relative speed between objects is greater than zero, that is to say, as long as there is relative uniform motion between objects, then the time dilation and distance contraction phenomena will be at work, directly affecting these objects, although, as we’ve seen, these effects become noticeable only at significant fractions of the speed of light.

As we stated earlier, this symmetry appears to be paradoxical, and we may well be inclined to ask, as we did previously when Scotty’s T.O. Special roared through the train crossing where we were standing, “which frame of reference, then, is the ‘correct’ point of view?” Strictly speaking, since the two frames are in relative uniform motion with respect to each other, that is, motion in a straight line and at a constant speed, then the laws of physics do not ‘favour’ one frame over the other. The laws of physics behave exactly the same way in either frame. Therefore, with regard to the space station and the spaceship, neither of the two sets of observers, we nor the astronauts, has the privilege to conclude that, “Yes, we are definitely the ones who are moving!”, and thus, the most that can be said by either party is that, “We and the other frame of reference are in uniform motion relative to each other.” Hence, since we are strictly speaking only about relative uniform motion between reference frames, then we must conclude that both points of view are equally correct! But from this very conclusion arose an apparent logical inconsistency, which was brought to light by several physicists shortly after Einstein published his special^[2] theory of relativity in 1905, in what was coined “The Clock Paradox”, which was later given its more famous name, “The Twin Paradox”. The focus of this argument, as we might have already surmised, was directly on the apparent paradoxical nature of the symmetry of the time dilation phenomenon. However, as we shall discover, the term ‘apparent’ is quite appropriate, because once we comprehend the full picture, no paradox actually exists! To do so, we must, in our later discussions, take a more detailed look at the distance contraction phenomenon, and then, examine perhaps the strangest, most unexpected, but most aesthetic consequence of the special theory, namely, the relativity of simultaneous events. And so, once again, let’s be prepared to hold on to our false teeth!

On a final note, we can use the inverse of the time dilation factor (i.e., the quantity

which is the inverse of

to directly calculate corresponding time intervals, that is, time durations, between two frames of reference that are in relative uniform motion with respect to one another.

For example, if the spaceship zooms past our space station at a relative speed of 0.9798c, then we will observe that the astronauts’ clocks are ticking at a rate that is

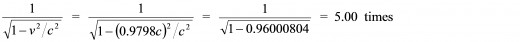
slower than our clocks. Therefore, if a time interval of Δt_STATION elapses on our clocks here on our space station, then we will observe a lesser corresponding time interval of only

elapse on the astronauts’ clocks. But we take notice of the fact that the value ¹/_5.00 is the inverse of the time dilation factor, whose value is 5.00. And if we call the (lesser) corresponding time interval that we had observed to elapse on the astronauts’ clocks Δt_{ASTROS AS SEEN BY STATION}, then clearly, from our point of view, the relationship between these two time intervals is given by the equation

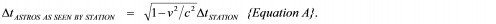
And checking the validity of {Equation A} by substituting the value of the relative speed directly into the equation, yields

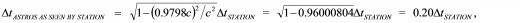
which is exactly the result we obtained above. But of course, because of the symmetry of relativity, from the astronauts’ point of view, they will observe that it is our clocks that are ticking 5.00 times slower than theirs instead, and hence, from their perspective, this relationship between corresponding time intervals must be given by the completely symmetrical equation

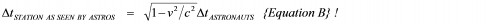
Okay, time for a quick example that will hopefully shed more light on and clear up this last area of our discussion. Let’s say that a second spaceship blazes past our space station again, this time at the hair scorching relative speed of 99.499% of the speed of light, that is, 0.99499c. From the astronauts’ point of view, they are at rest, and it is our space station that is moving past them at 0.99499c instead. On board their stationary spaceship, the astronauts let 180.0 seconds of normal time elapse on their clocks.

The question is, then, what corresponding time interval will the astronauts observe to have elapsed on our clocks on the moving space station? Well, from the astronauts’ perspective, clocks on board the ship must, as pointed out above, be ticking at the normal rate of time passage, since the astronauts have every right to claim that they are the ones at rest, and also, since the ship’s clocks are, of course, stationary relative to the astronauts. Consequently, the astronauts will observe clocks on our moving space station to be ticking at a slower rate than normal. Now, from {Equation B}, we know that

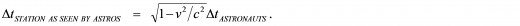
Thus, simply substituting the known quantities into the equation gives us:

Therefore, the astronauts will observe a corresponding lesser time interval of only 18.0 seconds to have elapsed on our clocks on the space station!

Now on the other hand, if we observe a time interval of Δt_{ASTROS AS SEEN BY STATION}, elapse on the astronauts’ clocks, then we, who consider ourselves (on board our space station) to be at rest, will therefore observe a greater corresponding time interval of

elapse on our clocks here on the space station (we are just re-arranging Equation A). And substituting v = 0.9798c, from our original example, for the relative speed between the spaceship and the space station, we of course obtain the result that

because we observe their clocks ticking 5.00 times slower than ours. But not to be outdone, if the astronauts observe a time interval of Δt_{STATION AS SEEN BY ASTROS} elapse on our clocks, then from the astronauts’ perspective, who consider themselves to be at rest, it therefore follows that

(we are just re-arranging Equation B), because of relativity’s symmetry. And substituting v = 0.9798c once more for the relative speed between our space station and the spaceship, we of course obtain the completely symmetrical result that

because the astronauts observe our clocks ticking 5.00 times slower than theirs instead!

Okay, time for one final example – finally. Let’s say that a third and final spaceship zooms past the space station, again at the relative speed of 0.99499c (where are all of these astronauts going? Is there a poker tourney on Pluto that we aren’t aware of ?…). We see their ship fly by, and we observe a time interval of 30.0 seconds elapse on their ship’s clocks before they decide to draw their window blinds and head home to Pluto, so as to take part in the Solar System Series of Texas Hold ‘Em.

Now, the question is, what corresponding time interval will we observe to have elapsed on our clocks here on the space station? Well, from our point of view, we are at rest, and it is the spaceship that is moving past our space station at 0.99499c. Hence, we will observe that clocks on board their ship are, of course, ticking at a slower rate than normal, while our clocks on the space station will be ticking at the normal rate of time passage (since our clocks are stationary, relative to us). And, from re-arranging {Equation A}, we know that

So again, simply substituting the known quantities into the equation gives us:

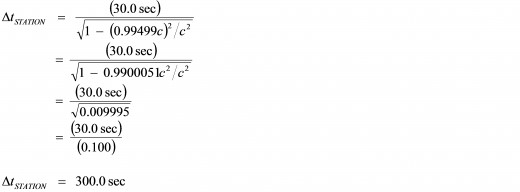
Therefore, we will observe a corresponding greater time interval of 300.0 seconds to have elapsed on our clocks here on the space station! And as a matter for observation, we notice that for both of our examples, the relativistic time dilation factor has a value of 10. This is because both examples use the same value of 0.99499c for the relative speed between the two frames of reference!

Thus, if we carefully analyze these latest calculations and examples, we can conclude that the inverse of the time dilation factor is (also) a ratio that can be thought of as having the following meaning:

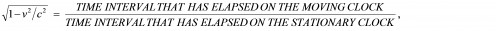
as seen from the point of view of the stationary observer.

Now, looking at our equation, let’s do a little re-naming to make things simpler. Let us call the “TIME INTERVAL THAT HAS ELAPSED ON THE MOVING CLOCK” Δt_MOVING, and the corresponding “TIME INTERVAL THAT HAS ELAPSED ON THE STATIONARY CLOCK” Δt_STATIONARY. Hence, our equation for the inverse of the time dilation factor becomes

(from the perspective of the stationary observer), which is much easier to read! But as we know all too well by now, relative to an observer, a moving clock always ticks more slowly than a clock that is stationary. Consequently, the amount of time, Δt_MOVING, that elapses on the moving clock will always be less than the corresponding amount of (normal) time, Δt_STATIONARY, that elapses on its stationary counterpart. And because this relation,

is always true for two clocks that are in uniform motion relative to each other, then the value of the ratio

must always be less than 1, from the viewpoint of the stationary observer. Therefore, the value of the quantity

that is, the inverse of the time dilation factor, must also always be less than 1, from the viewpoint of the stationary observer.

But, with all of this “motion – commotion” going on, who, exactly, is the stationary observer? Is it us? Is it Scotty? How about those ‘fuzzy’ little muons? Or perhaps it’s the astronouts? Who is it? Indeed, we’ve got a pretty good grip on the crux of special relativity, if we can answer this question without reading any further. Nonetheless, we must answer this question, as it cuts straight to the core of Albert Einstein’s remarkable theory. Hence: Since our entire discussion has been strictly concerning relative uniform motion, then by special relativity’s first postulate, namely, the principle of relativity, we (hopefully) now know that: any and all observers can consider their respective reference frames to be at rest, that is, stationary! We, Scotty, the muons, the astronauts, paramecium, amoebae, big rocks and small rocks – any and all observers, provided that they are in relative uniform motion – can assert that they are the stationary observers, and it is the other observers or objects that are moving instead! Therefore, the equation for the time dilation and length contraction factor, along with the equation for the inverse of the time dilation factor, must apply from the viewpoints of any and all observers in relative uniform motion! And as a direct result of this fact, everyone will claim that they possess the fastest ticking clocks and the longest measuring rulers in the universe! And so, Einstein indeed discovered the truth that, as far as relative uniform motion is concerned, all observers are created equal! Tally – ho!!

We close our current discourse with a quote from Einstein himself, from the book “The Evolution of Physics” (1938), which he co-authoured with L. Infeld, that summarizes our findings quite nicely.

“In classical [Newtonian] physics it was always assumed that clocks in motion and at rest have the same rhythm, that rods in motion and at rest have the same length. If the velocity of light is the same in all coordinate systems, if the [principle of] relativity… is valid, then we must sacrifice this assumption. It is difficult to get rid of deep-rooted prejudices, but there is no other way.”

[2] The reason for the word “special” in the special theory of relativity is that the theory is an analysis of the effects of only a certain type of motion, specifically, uniform motion – motion in a straight line and at a constant speed. But there is also accelerated motion, in which the speed changes its direction and/or magnitude over time, such as the motion that we feel when our muscle car takes a tight corner, or as it accelerates from zero to sixty on the drag strip. In 1916, Albert Einstein published his masterpiece, the general theory of relativity. It encompassed accelerated motion and subsumed special relativity, but very much more, it was a radical new theory about the inner workings of the gravitational force, which, until then, had no “how gravity actually works” manual. It was Einstein’s insight that one cannot distinguish the effects of accelerated motion from those of a gravitational field – which he would later call the “happiest thought” of his life – that showed him what his end result must be. For instance, if we were in a windowless elevator somewhere out in deep space where gravity was absent, and if the elevator was accelerating “upward” at the constant rate of one g, then the effects that we would experience in the elevator would be indistinguishable from the effects that we would experience standing on the surface of the earth, where gravity is present. We would feel the floor of the elevator pressing up against our feet, just as the surface of the earth presses up against our feet. If we were to let go of an object, say a billiard ball, it would ‘fall’ to the floor of the elevator with increasing speed, in exactly the same way that an object dropped from a height would fall to the surface of the earth with increasing speed. According to Einstein, the effects of accelerated motion are equivalent to those of gravity. Now, applying special relativity’s time dilation and distance contraction phenomena to analyze the effects that accelerated motion has on space and time, he discovered that, from the point of view of the accelerating observer, accelerated motion bends space itself, and warps time itself. Furthermore, a greater acceleration produces a greater bending and warping, or “curvature”, of “space-time”. Hence, with this analysis, Einstein was able to make the final brilliant and intrepid link in his logic, asserting that since accelerated motion and gravity are equivalent, and since acceleration curves space-time, then gravity itself must also be the curvature of space-time. It took him ten years of intense, and at times tormented thinking to mathematically achieve this end result. According to the general theory of relativity, then, gravity is not some mysterious, instantaneous attractive force between objects, but rather, gravity is the curvature of space and the warping of time caused by an object’s presence, whose influence is propagated at exactly the speed of light. And it is this curving of space-time by the presence of mass that causes the “attractive” force between all objects, with a greater mass, just as with a greater acceleration, producing a greater curvature of space-time, thus producing a greater “attractive” force. Hence, our earth is following a path in the curved space-time created by the sun, as it orbits. And the moon is, in turn, following a path in the curved space-time created by the earth, as it orbits us. To aid with the ‘visualization’ of this curvature, physicists often use the analogy of a heavy bowling ball that is placed at the centre of a stretched – out, flat rubber sheet, with the sheet itself representing space. The presence of the ball warps the surface of the sheet, creating a curvature that is greatest nearest the ball, which then becomes less and less as the distance from the ball increases. Now, if a small marble is rolling in the vicinity of the heavy bowling ball, then it will follow the curved path created by the ball and ‘orbit’ the bowling ball. However, this is an extremely simple analogy at best, because to begin with, Einstein first had to deal with how the presence of mass curves our three dimensional space and warps the passage of time, and then, as if that were not enough, he had to deal with what the combined effect of this curvature of three dimensional space and this warping of time has on the motion of material bodies! His theory has correctly predicted the motion of objects in our vast universe (and the trajectory of light itself!) where Newton’s theory of gravity has failed, as once more, Newtonian gravity is only accurate when dealing with objects of comparatively small mass, which are traveling at relative speeds much less than the speed of light. The true essence of Einstein’s genius lies is the fact that there was absolutely no experimental evidence that existed, at the time, that he could use to guide him in formulating the general theory, although he knew that for very small (i.e., everyday) relative speeds, the general theory’s equations had to transform into Newton’s equations of gravity and motion as a limiting case. Hence, having only his single elegant premise – that one cannot distinguish the effects of accelerated motion from those of a gravitational field – and his special theory to build upon, he created the general theory using pure thought and reason alone! Einstein’s general theory of relativity continues to be the theory of gravitation in use to this day, passing all rigorous tests that have been thrown its way. It is one of the two fundamental pillars of modern physics (the other being quantum mechanics, for which Einstein also helped to lay the foundation!), and is considered by many to be the greatest individual intellectual achievement of all time.