Factorising quadratic expressions, and solving quadratic equations
Needed for:
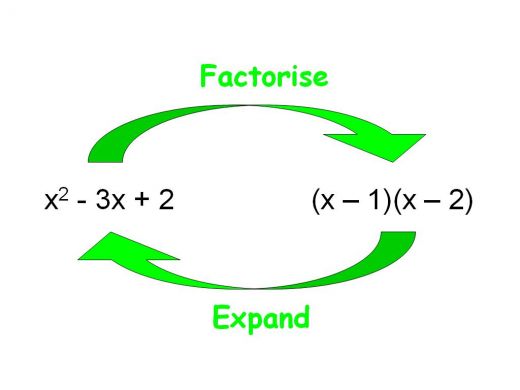
What do we mean by factorising?
Factorising - or factoring, to non-British English speakers - is the process of breaking an expression into its factors.
You may have seen how to factorise a linear expression by taking out a common factor:
2x + 4 = 2(x + 2) as 2 is a common factor of both 2x and 4.
This process is the opposite of expanding the bracket - and the same is true for quadratics.
What does "quadratic" mean?
A quadratic is an algebraic expression where the highest power of the unknown variable is 2 - in other words, anything in the form ax2 + bx + c. Generally, we write them in descending order; the x2 term first, then the x term, then the constant c.
Useful links:
- Explore: MathsNet
Interactive graph of y=(x-a)(x-b). Play with the values and see what happens - use the coloured squares at the top-right to change interactives. - Activities: GCSE Bitesize
Notes and activities for UK GCSE students, from foundation to higher tier, including the Quadratic Formula. - Notes: mathsrevision.net
More notes on expanding and factorising quadratics, as well as the difference fo two squares - Practice: Interactive Algebra
Practice your skills with increasingly complex questions and step-by-step answers. - Notes: Solving by Factoring
Demonstrates how to solve quadratics using factorising in more detail than this guide.
Factorising as the inverse of expanding
When you worked on expanding a double bracket (x + a)(x + b), you may have noticed that:
- The numbers in the brackets always add up to the number of "xs," or the "coefficient of x."
- The numbers in the brackets always multiply to make the +? on the end, or "the constant term."
If we expand (x + a)(x + b) we get x2 + ax + bx + ab, or x2 + (a+b)x + ab - which supports the observations above...
So, to factorise a quadratic we need to find two numbers that add up to the x coefficient, and multiply to make the constant on the end. For example:
"Factorise x2 + 7x + 12"
We need two numbers that:
- Sum to 7
- Have a product of 12
From this we can (hopefully) see that the numbers we need are 3 and 4.
Top tip: Look for factors of the constant first, as there are a finite number of possibilities! In this case, the only possible integer pairs are: 1 & 12, 2 & 6, 3 & 4, -3 & -4, -2 & -6, -1 & -12. Then find the pair that sum to the number you need.
So how do I solve quadratic equations?
The "solutions," or roots, of a quadratic are the values of x where the graph would cross - or touch - the x axis. In other words, they are the x values that make the whole equation equal zero.
Because we are multiplying our two linear factors (the pair of brackets) together to make our quadratic, we can make the whole expression zero by making either bracket zero; anything multiplied by zero is still zero!
So to solve x2 + 7x + 12 = 0:
- Factorise: (x + 3)(x + 4)
- What x value makes the first bracket zero? -3 + 3 = 0, so x = -3.
- What x value makes the second bracket zero? -4 + 4 = 0, so x = -4.
This means our roots are x = -3 and x = -4. If you plotted the graph of y = x2 + 7x + 12, it would cross the x-axis at these points.
If you have a quadratic that won't factorise, you need to learn the Quadratic Formula - but it's not too hard!