Finding the factors and roots of a polynomial equation
Builds on:
Needed for:
What do we mean by "polynomial?"
Polynomial expressions are ones that have different powers of the same variable in, for example quadratics (or trinomials to Americans?) have an x2 term, an x term and a constant - cubics have an x3, an x2, an x and a constant. And so on...
The roots of a polynomial expression f(x) are where the graph of y = f(x) crosses the x-axis, or the values of x that make the expression equal to zero.
The simplest case of this would be factorising a quadratic equation in order to solve it, but the principles apply to all polynomials.
Factorising cubics
Cubic expressions, having x3 as the largest power of x, can be thought of as the product of a quadratic and a linear expression:
(x + n)(ax2 + bx + c) would give a cubic expression as the highest possible power of x would be given by multiplying the x term in the first bracket by the x2 term in the second.
You would generally be given the linear expression in the question, so the question becomes: how do we find the values of a, b, and c in the quadratic?
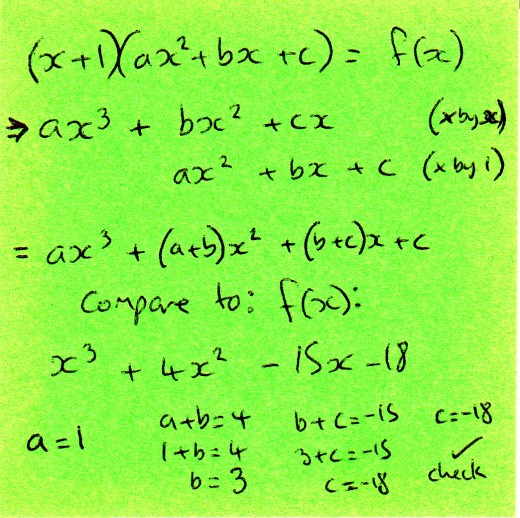
- Notes: University of Warwick
An excellent PowerPoint that breaks down the method described here, and shows an alternative too. - Alternative: Long division
You could also divide the cubic by the linear expression using "algebraic long division" - here's how! - Practice: Cool Math
Practice your polynomial skills online - bags and bags of activities here!
Comparing coefficients
If we know the linear expression that is a factor of our cubic, and the cubic expression we are trying to find the roots of, we can simply expand the brackets above and compare our coefficients - for example:
"Given that (x + 1) is a factor of f(x) = x3 + 4x2 - 15x - 18, solve f(x) = 0"
We multiply our (x + 1) by a "dummy" quadratic ax2 + bx + c to see how many of each power of x we get - we then compare the coefficients to f(x) in order to find the values of a, b, and c in our quadratic. See image!
Personally, I find it easier to multiply through by each term in the linear factor separately, and write the x3, x2, x and constant terms together - but that's just me.
We can then factorise the quadratic normally to find the missing roots.
In this example, the quadratic we need would be x2 + 3x - 18 (given the values of a, b, and c in the image above) which factorises to (x - 3)(x + 6), so our three factors are (x +1)(x - 3)(x + 6).
Our roots are whatever x values make f(x) = 0, which we can do by making each bracket zero - just like solving a quadratic. This gives x = -1, x = 3, and x = -6. This is where the graph of y = f(x) crosses the x-axis, if you want to check!
What if you're not given the linear factor?
Any linear factor of a polynomial can be found using the Factor Theorem, which is really just a special case of the Remainder Theorem - but that's another story!