How to Add Fractions With the Same Denominators

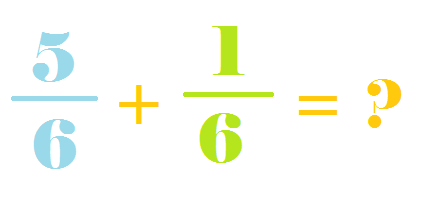
Adding fractions with like denominators is very easy to learn and even easier to do! When adding fractions together, keep in mind these terms. The numerator is the number on top of the fraction bar and the denominator is the number on the bottom of the fraction bar.

When a fraction has the same denominator, it is referred to as having common denominators. Fractions with common denominators will have the same number as their denominator. For example, the fraction 4/5 and 1/5 have a common denominator. The same goes for 4/5 and 2/10. When you are dealing with fractions, it is easy if you reduce the fraction to simplest terms. When you reduce 2/10, you get 1/5. Always remember to reduce the fraction as it will make math involving fractions a lot easier.

Adding fractions with a common denominator is very simple. Remember, fractions with a common denominator will have the same number as their denominators. Because the fractions have common denominators, we can ignore them.

Let's say you have the problem 1/4 + 3/4.

• Since they have common denominators, we can ignore the /4.
• Now you have 1 + 3. Solve.
• 1 + 3 is 4. Therefore, the new numerator is 4.
• Plug in the denominator again to make it a fraction.
• The new fraction is 4/4. Don't forget to simplify.
• The new fraction is 1/1 or, simplified even further, 1.

Fractions are not whole numbers. Fractions are a part of a whole number. 1/10 is 10% of 1. That being said, the denominator can be imagined as the item you are counting. I have 1 piece of a 10.

Let's say you have the problem 1/10 + 3/10.
Let's add the numerators. 1 + 3 is 4. The new numerator is 4.
Now, for the sake of this example, let's add the denominators.
10 + 10 is 20. Oh look, the new denominator is 20.

By adding the denominators, I have created a new "item". It is no longer a piece of a 10. They have become a piece of a 20.

To put it another way, you wouldn't put 2 cupcakes together and say they made cake (although that would be awesome). You would still only have 2 cupcakes.

If you are adding numerators, one of these times the numerator is going to be greater than the denominator.

Let's say you have the problem 1/5 + 4/5 + 2/5.

• Even for problems with 3 or more fractions, the process is the same.
• Ignore the denominator and pay attention to the numerator.
• 1 + 4 + 2 is 7.
• Now let's plug in the denominator. Our new fraction is 7/5.

7/5 is not the right answer. This is what we call an improper fraction. Even though you cannot reduce 7/5, it is still not in it's simplest form.

Remember, a fraction is signifying a part of the whole. If I have 3/5, I have 3 parts of 5 pieces that make a whole number. If I had five 1/5 pieces, I would have a whole number.

Let's go back and look at the fraction 7/5.

• If you imagine this as pizza slices, I have 7 slices of pizza. 5 slices make a whole.
• If I put all 5 slices together, I will have one whole and 2 slices.
• In fraction terms, that is the same as 1(2/5). I have one whole number and 2 leftover 5 pieces.