Algebra: The Elimination Method
system of linear equation problems

The elimination method
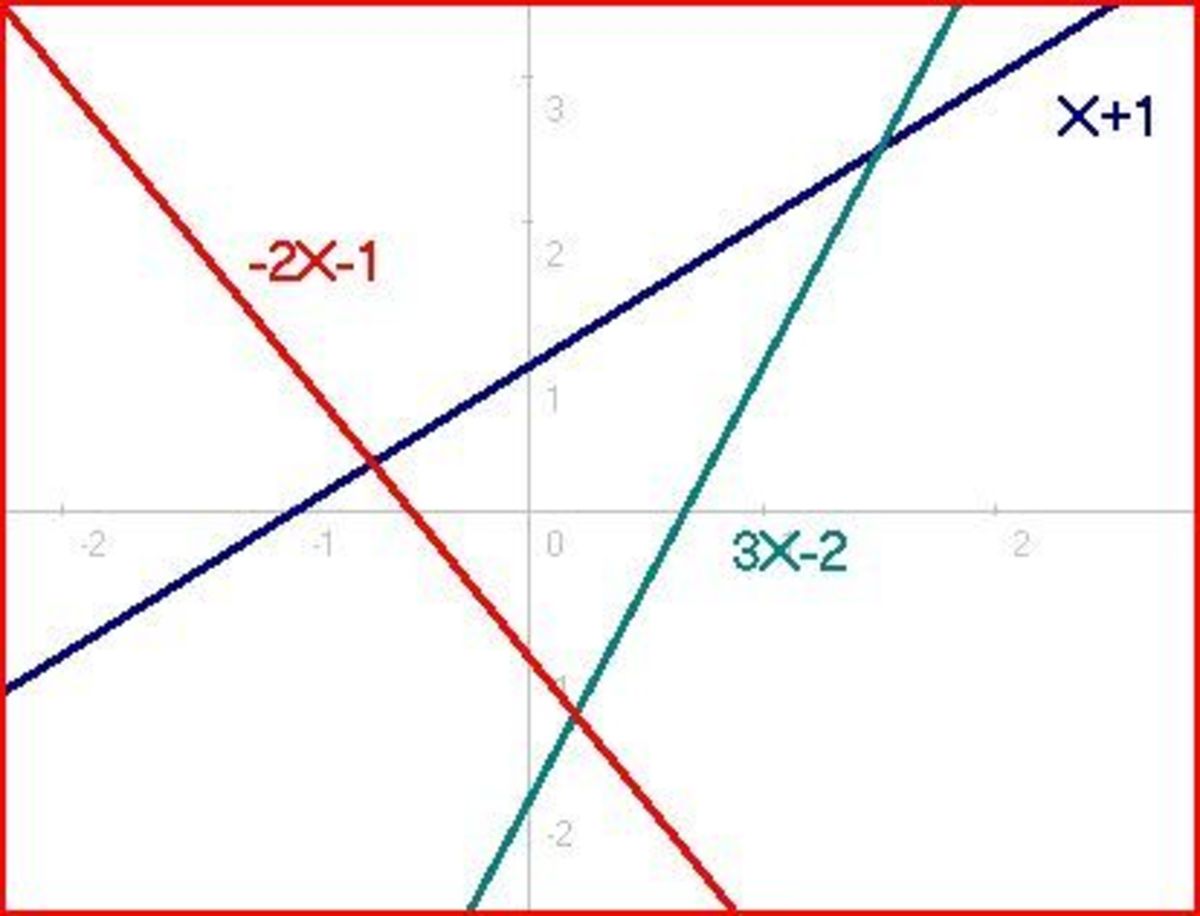
If you read my article on the substitution method, you know that when I first was taught how to use this method in class I was confused about what I learned. And when I looked online I could never find anything on how to use the elimination method. This is another method that can be used to solve a system of linear equations, along with the substitution method and the graphing method. The answer should be at the coordinates at which the two equations would meet if they were graphed. And there are three types of answers you can receive from a system of linear equations. First, you may find that the system has one specific answer, you should find one coordinate where they would meet on a graph. Next, you may find that the system has unlimited solutions, in this case they will be the same two lines. Finally, you may find that there is no solution, the lines will be parallel to each other when they are graphed. Now that we covered that i'll show you how to use the method.
A graphed system of linear equations
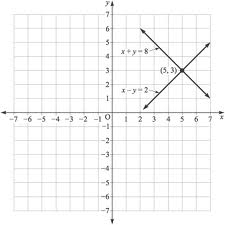
How to use the elimination method
Now i'm going to use the elimination method to solve the system of equations: X+2Y=-1 and 4X-4Y=20, you may want to follow along on a piece of paper as well. The first thing you do is take the first equation and multiply both sides by two. The equation should now read: 2X+4Y=-2 and then you do something weird (at least it seemed weird the first time I heard this) you add the equations. 2X+4Y=-2 + 4X-4Y=20, 2X and 4X and 6X the 4Y and -4Y cancel each out and -2 and 20 equal 18. So you have 6X=18 to get X by itself you divide each side by 6 and you find X=3. Then you take the original first equation and substitute three in for X: 3+2Y=-1. minus three from each side and you have 2Y=-4 divide each side by 2 and you find Y=-2. Then you take the second equation and substitute in both three for X and negative two for Y so you have 4(3)-4(-2)=20. Multiply 4 and 3 to get 12, and -4 and -2 to get 8, you now have 12+8=20. And this is true so we know that the answer we have come up with is true, so (3,-2) is correct. Also above you can use the second equation to find the second variable then use the first equation to check your answers It doesn't matter as long as you don't use the same one twice.
How to find a system with no solution or infinite solutions
When going through an equation when finding your first variable you may find something such as 8=2 or 16=16. If the statement is true, the 16=16, then the lines are the same and the system of equations has infinite solutions. If the the system comes out with something that is false, such as 8=2, then the lines are parallel and there are no solutions to the system. This is the end, I hope this helps you understand how to us the elimination method I also have a hub on the substitution method here is a link if you want to check it out: http://greekwarrior.hubpages.com/hub/How-to-use-the-substitution-method