Algebra: The Substitution Method
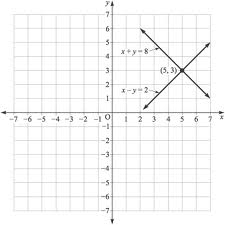
A system of linear equations
The substitution method
When I first learned how to use this method I left class confused and couldn't figure out how to solve the problems. And I couldn't really find anything online that would help me with it either so, now that I understand it, I though i'd write my own guide on how to use this. This is one of the methods that can be used to solve a system of linear equations simply put. This is where two lines would meet if the two lines were graphed. There are three different types of answers you can receive from this, the first is you can find the system has no solution, it meets nowhere on the graph and the two lines will be parallel to each other. Next, you may find that the graph has infinite solutions, in this case the two lines are the same line. And finally, you can find that the graph has one specific answer and it meets at one location on the graph.
Here is a link to a hub on how to use the elimination method:
http://greekwarrior.hubpages.com/hub/How-to-use-the-elimination-method
Solving a system of linear equations
Now i'll show you how to solve a system using the substitution method. I'll solve the problem: X+2Y=-1 and 4X-4Y=20 feel free to follow along on a piece of paper, the first thing you should you do is take one of the two equations we will take the first one X+2Y=-1. Now subtract 2Y from each side to find X you should have X=-2Y-1. Next, you take the second equation: 4X-4Y=20 and substitute -2Y-1 into the equation in place of X because we know that X is equal to that. You should have 4(-2Y-1)-4Y=20 then distribute the four to the 2Y-1 and get -8Y-4-4Y=20. Then add four to each side and you get -8Y-4Y=24 then combine like terms and you find -12Y=24. Then divide -12 on each side and finally you have Y=-2 and you substitute Y into the first equation. You now have X+2(-2)=-1 multiply 2 and -2 to get X+-4=-1 then add four to each side and you figure out X=3. Now you know that Y=-2 and X=3 substitute each of these into the second equation to check to make sure that what you got is correct. Now you have 4(3)-4(-2)=20 multiply 4 by 3 and -4 by -2 you should have 12+8=20 which it does so you know that the answers you got are truly correct. When your solving the equations make sure that you alternate between the first and second equation like I did above. Start by figuring out one other way to write a variable (X or Y let's say we find X) using the first equation then, substitute it into the second equation to solve the other variable (Y). Next, substitute the answer to that variable (Y) into the first equation to solve the other variable (X). Finally substitute both variables (X and Y) into the second equation to check your answers. You can also switch everything and start with the second equation then go to the first and so on and also the first variable you find can be Y I just used X in the example.
Now try to solve this systems of linear equations now:
1. Y=2X and 2X+Y=8
Answers
1. X=2 and Y=4
2. 8=8, infinite solutions
Infinite and no solution
When your solving a problem you may find that the variables cancel each other out when you combine like terms. When solving a problem you don't figure the answer to a variable but, you find something like 2=3 or 4=4. If this happens the answer is either no solution or infinite solutions. When what you get is true for example 4=4 then their are infinite solutions and the lines are the same. And when what you get is false, like 2=3, then the answer would be no solution, the lines are parallel and they never meet on the graph.
Now that you know this, try the following problem
2. X-5Y=2 and 4X-20Y=8