Log, Ln, e --The World of Logarithms/Problems and Applications
If you've ever seen this rover "Curiosity" that landed on Mars on August 6, 2012, chances are, NASA made use of complex binary algorithms. Let's put it simply this way: the rover was already going down on Martian surface with critical tasks of survival; last second decision making was handed by powerful computers, that put into practice that yes/no input/output.
Of course, we as general public/viewers saw it as another historical event, but behind all that awesomeness there was math, and logarithms for sure.
Just considered HubPages for a second. Those buttons for flagging, voting up/down are essentially handled by logarithmic formulae. There is an intrinsic association between logarithms and algorithms. The whole math involved in it can take us back to those flowcharts that involved commands like, If, GoTo, loops and of course "start" and "end." We are writing a more popular view of this torture of math. In real life we talk about getting input and delivering an output. Let's see what we have store:

What The Heck is This Number "e"?
If you ask Mark Zuckerberg, you will be asking about a God for him. Is a number he needed in his algorithmic ideas to start FaceBook. Silicon Valley think of this number as magical, but what is it?
e= 2.7182
Was named Euler's constant in honor of Leonhard Euler (1707-1787), a Swiss Mathematician that loved his math like us.
If you want a more accurate number here it is
e=2.71828182845904523536028747135266249775724709369995.
But, what is it, Lord?
Is a constant number obtained from this sumatory : Σ (1 + 1/n)n for n=∞ or infinite.
It was chosen as the base for napiers natural logarithm ln with base e.
An example of this sum of infinite series is shown below.
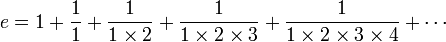

Logarithm : Definition
John Napier introduced the name and its definition on His work, Mirifici Logarithmorum Canonis Descriptio (1614). Back then you had to write everything in Latin, and carefully spell the name of the King of the day whom the written piece would be dedicated to, with all kind of silly eulogies, sort of kissing their butt... but let's go straight to business:
Logarithm - ROUGH DEFINITION
The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For instance, you have the number 10,000 and you have a base of 10. You want to find the number x where:
10x =10,000
Common sense will indicate that x=4, but mathematicians wanted to make it look better and more academic... oh Gosh! Please, Sir John Napier and Monsieur Euler!
logarithmorum10 (10,000) = 4 (this nomenclature was understood in 1614-1615)
Right away it was shortened to "log"
Today, we recognize it better like this:
log10 (10,000) = 4
Napier, found that e=2.7182 was a more natural base than our base of 10 (100, 1000, 10,000)
LN is born
Smart enough, Napier squeezed his last name in the natural logarithm 'ln' (logarithmun naturalis). Why is better than 10? Well, life is based on natural increments. If you borrow money from the bank, the interest yielded will be based on this powerful number--Sort of π for "Geo" and "Trigo." I see those young kids saying..."ew! Now Lord is getting on our nerves!"
Life is not based in rigid numbers of 10, 20 or 30's. Don't want to go deeper, because then our brain will blow, before the end of this article. So help me God!

Practical examples:
Solving algebraic equations involving logarithms
We are skipping some hard math and go straight to the point in here: Math can be harder enough if you follow your teacher's somber archaic methods.
We want to make sure we know this logarithm identities for further use.
log(a*b) = log(a) + log(b)
log(a/b) = log(a) - log(b)
log(ab) = b*log(a)
log(1) = 0 because 100=1 here and in China. Please, math is not a joke!
Any base to the power of the logarithm with the same base will cancel the base and the logarithm. This is the beauty:
-
10 log10(x) = x
-
e ln(x) = x
EXAMPLE 1
log(5x+1) - log(x-5) = log(20) (base of 10)
If we make use of the trick of the relation : 10 log10(x) = x then we are getting somewhere:
Let's shortened the equation into an easier one
log((5x+1)/(x-5)) =log(20)
10 log(5x+1/X-5) = 10 log(20)
(5x-1)/(x-5) = 20 ( please Josh! You didn't pay attention? And you Jon?)
Now we have a more easier equation that happens to be linear (I know Miss Olive...I know! bear with us.)
5x-1=20(x-5)
5x-1=20x -100
moving x to the right side:
20x-5x=100-1
15x=99 x=99/15 x=6.6
Example 2
e(9x-5) - e (2x-1) =45
By using the relation: ln e x = x, we get rid of the monster equation and solve it!
lne(9x-5) - lne (2x-1) = ln (45)
ln(9x-5)/(2x-1)=ln(45) by simplifying we get:
(9x-5)/(2x-1)=ln(45) ; lets call ln(45)=k, by going to the natural log tables:
ln(45)= 3.8066624898 or 3.8, k=3.8
Solving the equation:
9x-5 =k(2x-1)
9x-5= 2xk-k
9x-2xk=5-k (almost done Josh!)
x(9-2k)=5-k
x=(5-k)/(9-2k) replacing k=3.8= ln(45)
we find x:
x=5-3.8/[9-2(3.8)]
x=1.2/(9-7.6)
x=1.2/1.4
x=0.857
We study this logarithms for nothing?
Certainly, if you want to be a scientist or chemist you will see it at the pH of any solution. Or perhaps at the Richter scale quake measurement magnitude formula; or behind the HP scoring...? You don't have to kill yourself by going any further. We are who we are. We all have unique qualities, and we all fit in the equation of life. But at least you got the hang of it, right?
This is not us....Just in case Tammy. Kelly, Ardie or Lathing ask...!
More fun math links...
- Pascal's Triangle For Dummies
Pascal's triangle is a triangle array of the binomial coefficients in a triangle. It is named after the French mathematician Blaise Pascal, but has been known from centuries. It was already known in India, China and Greece. We followed his steps goin - Who Created the Mathematical Symbols?
Going back in time with my 'young self,' trying to find out who the heck made these symbols just to torture our kids? - Pythagorean Theorem -- Applications On Real Time...!
Practical applications of the Pythagorean Theorem. Real time applications. - Geometric Sequences -- Real Life Applications
Practical and real life applications for geometric sequences.