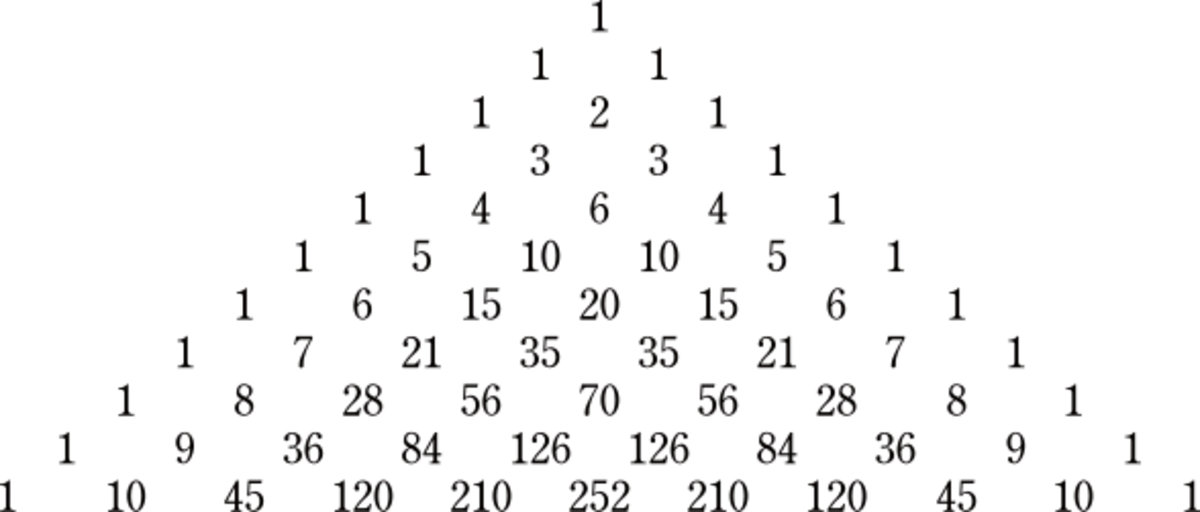Pascal's Triangle For Dummies

Pascal's triangle is a triangle array of the binomial coefficients in a triangle. It is named after the French mathematician Blaise Pascal, but has been known from centuries. It was already known in India, China and Greece.
For the western world is known as Pascal's triangle since 1730. Just take a look how the name array changes according to the country or continent:
Khayyam triangle in Iran, after Omar Khayyam a poet and mathematician from Persia (1048-1131 A.D.)
Yang Hui's triangle in China, after Yang Hui (1238–1298)
In Italy, it is referred to as Tartaglia's triangle, named for the Italian algebraist Niccolo Fontana Tartaglia (1500–1577)
Binomial Expansion
Given (a+b)n as an algebraic binomial to the nth power, we will have an expansion with some coefficients that can be found on the Pascal's triangle. For years we have been struggling for ways of memorizing this set of numbers in a triangle. After checking the original 'building block', we came out with an idea: Mnemonics and graphics.
Consider the expansion:
(x + y)2 = x2 + 2xy + y2 = 1x2y0 + 2x1y1 + 1x0y2
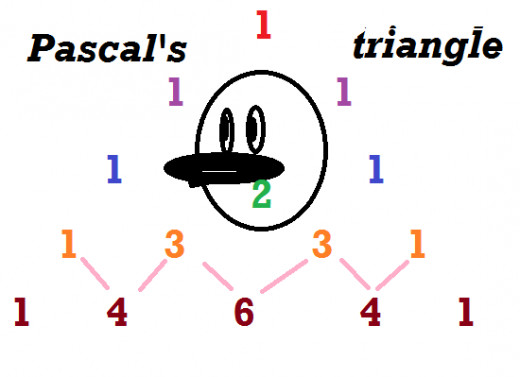
Pascal's triangle determines the coefficients which arise in BINOMIAL EXPANSIONS. For example we can build a triangle from scratch positioning our 'duck' on arrow #3. 'Duckier' will be surrounded by numbers 1.
Many High school students have had problems building this triangle. Our teacher would start with number 1 on top. Arrow 2 would be kind of useless but contained two number 1's as coefficients. Which now make sense to us:
(a+b)1 = 1a+1b
Using that duck in place, we can build Pascal's triangle all the way down with a solid foundation.
Bellow we have binomials to the power of 3, 4, 5,6 and 7. Notice the coefficients that follow the Pascal' triangle array with no problem.
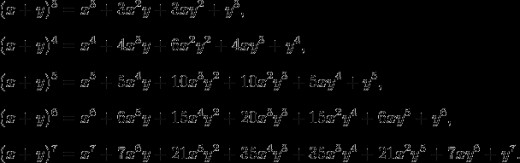
Now that you are able to take this graphic-algebraic expansion, we see that the sequence of coefficients on the "eighth arrow" will be like this:
1, 7, 21, 35, 21, 7, 1
How would you calculate (0.999)5 ?
In the next video, a teacher will talk about Pascal and a practical example... in real time.
Tip spoiler: (0.999)5 = (1- 0.001)5
Solving 0.0999 to the Fifth Power -- watch her trick

About Blaise Pascal
Blaise Pascal (19 June 1623 – 19 August 1662), was a French mathematician, physicist, inventor, writer and Catholic Philosopher. Blaise's father was a tax collector in Rouen, which made Blaise get used to calculations. Actually, at 19 he invented the mechanical calculator which was know as Pascaline. This way, young Pascal would help his father on the tedious accounting calculations. Unfortunately he died at 39 of age, due to tuberculosis and stomach cancer. His legacy was remarkable to engineering, science and philosophy.
Related hubs...
- Math problem...! What math problem?
Sometimes we feel sorry for our kids, especially those that never had a chance to have a tutor. We have technology and we have a will. We can be read in Bangladesh, and we can be seen in Santa Fe, Argentina. This monster called math can be insidious - SIMPLE ALGEBRA EQUATIONS-HOW TO SOLVE THEM
An unique way to solve a simple equation using fun and creative situations. Mnemonics at work. - HOW TO HANDLE A MATH PROBLEM
A very unique way to confront Math. A 5 minute REVIEW THAT PROMISE TO CHANGE YOUR LIFE. Practical tips for you to have. - SOLVING DIVISIONS THE EASY WAY
The esiest way to help our kids to grab divisions with an open mind, and gain coinfidence and build their skills with a solid foundation. - Why Is Math So Hard?
Self explanatory. Reasons why math is so hard. Insightful details for parents, teachers and our kids.