Logarithms: Help for a Great Algebra Mystery

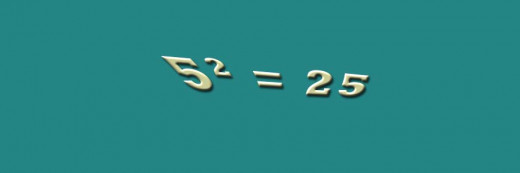
Of all the math topics that I have taught, it seems that logarithms are one of the most difficult for students to understand. While there may be many reasons for this, it seems to me the word "logarithm" is just too ominous, like a lion waiting to consume its prey. However, the mystery surrounding logarithms is really very easy to dispel. That is the purpose in this article.

The secret to working with logarithms is to realize that the term "logarithm" is a fancy term for exponent. When a person is working with logarithms, that person is simply working with exponents. The algebra student will remember working with the exponent rules. In essence, these rules are logarithm rules. The only real difference is with logarithms the focus is primarily upon working with the exponents rather than the base (bottom).

Certainly, no algebra student could argue with the fact that 4² = 16. This is generally read, "4 squared (or to the second power) equals 16." A little different rewording will move the problem into logarithms. If the wording is changed to "Two is the exponent that goes on 4 to produce 16" the original meaning is not changed. However, this gets us to a logarithm statement.

First, "Two is" means

2 =

Next, "the exponent" is the same as saying logarithm (we use log as an abbreviation)

2 = log

In the original statement 4 is the base. It is still the base, but since we are working with exponents (logarithms), we write 4 as a subscript.

2 = log₄

Finally, "to produce 16" is the inside of the logarithm.

2 = log₄16.

Now we have converted 4² = 16 (which is called exponential form) into 2 = log₄16 (which is called logarithmic form). The two statements mean the same thing: "Two is the exponent that goes on 4 to produce 16".

Another example would be 2^-3 = 1/8. "Two to the negative three power is equal to one-eighth" is the same as "Negative three is the exponent that goes on two to produce one-eighth". In logarithmic form,

-3 = log₂ 1/8

One more example would be 9^1/2 = 3. "Nine to the one-half power is equal to three" is the same as "One-half is the exponent that goes on nine to produce three." In logarithmic form,

1/2 = log₉ 3

Every algebra student needs to realize that logarithms are just exponents. There should be no mystery surrounding logarithms because they are something with which the algebra student is already familiar. But understanding this relationship will help the student in higher level mathematics to solve equations involving variable exponents. The mystery has been revealed.

1. Purple Math

2. Math Geek

3. Math.com

4. Interact Math