Factoring: The Holy Grail of Algebra
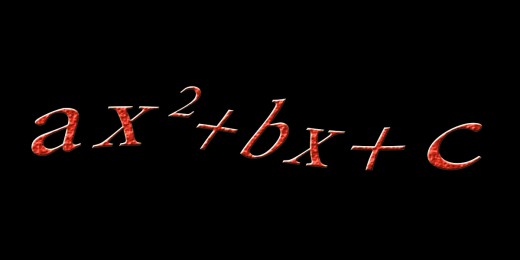
Students have always found factoring to be a thorn in their side. In my experience this is usually because of bad teaching or an overwhelming fear of the subject. Whenever I teach factoring I find myself battling these two causes rather than actually guiding students through factoring. In my opinion, one of the most harmful things a teacher can do to a student is teach the trial-and-error method of factoring. Throughout algebra we teach step-by-step logical procedures. Then along comes the trial-and-error method and we tell students to stop thinking logically and just guess until they get it right. Something is not right about that.
The Logical Path -- Factoring by Grouping
In my algebra classes, I only teach the factoring by grouping method. It is a logical, step-by-step procedure that most students can follow. The steps are listed below. This procedure assumes there is no Greatest Common Factor (GCF).
Given ax2 + bx + c,
1. Find a*c. Yes, this a simple step of multiplying the coefficient on x2 and the constant.
2. Find two numbers that multiply to the same number found in step one AND that add up to b. This is the step where most mistakes are made. If a pair of numbers cannot be found, the trinomial is not factorable in the rational numbers.
3. Break the middle term bx up into two terms using the two numbers found in step two as coefficients. This is why the two numbers had to add to b, because we are breaking b up.
4. Factor by grouping. After step three, you now have four terms. Put parentheses around the first two and around the last two and continue with factoring by grouping.
Students grasp this method far more easily than just guessing. The next section will show some examples.
Example 1
Suppose we have the trinomial 10x2 + 17x + 3. Thus, a=10, b=17, and c=3.
1. Find a*c = 10*3 = 30.
2. Find two numbers multiplying to 30 AND adding up to 17: 15 & 2 (Incidentally, it does not matter which is first).
3. Break up 17x into two pieces using 15 & 2 found in step 2: 10x2 + 15x + 2x + 3.
4. Factor by grouping: (10x2 + 15x) + (2x + 3)
5x(2x + 3) + 1(2x + 3)
(2x + 3)(5x + 1)
So 10x2 + 17x + 3 factors into (2x + 3)(5x + 1).
Example 2
Suppose we have the trinomial 6x2 + 7x - 3. Thus, a=6, b=7, and c= -3.
1. Find a*c = 6* -3 = -18.
2. Find two numbers multiplying to -18 AND adding up to 7: -2 & 9 (It does not matter which is first).
3. Break up 7x into two pieces using -2 & 9 found in step 2: 6x2 - 2x + 9x - 3.
4. Factor by grouping: (6x2 - 2x) + (9x - 3)
2x(3x - 1 ) + 3(3x - 1)
(3x - 1)(2x + 3)
So 6x2 + 7x - 3 factors into (3x - 1)(2x + 3).
Prime Example
A polynomial that is not factorable is called prime. When factoring trinomials, you will be able to tell in step two whether it is prime or factorable. If you cannot find a pair of numbers that meet both qualifications in step 2, you probably have a prime polynomial. For example, suppose we have x2 + 8x + 1. So a=1, b=8, and c=1.
1. a*c = 1*1 = 1.
2. Find two numbers multiplying to 1 and adding up to 8. It cannot be done. So the trinomial is prime.
Summary
This has been a brief tutorial on the factoring by grouping method for factoring trinomials. This method is a step-by-step procedure that gets factoring done correctly. Once again, the critical part is step two. There is only one pair of numbers that meets the qualifications (if the trinomial is factorable). Students often make mistakes because they hurry through this step and do not get the right two numbers. Nevertheless, this is the easiest method of factoring trinomials an algebra student can have.
For online math help, check out:
Other Math Articles:
- Learn Math: Online Problem Help
The Internet is full of online math problem help. In this article I review some of my favorite places which I recommend to my students. - Factoring by Grouping: Help with Four Term Polynomia...
Factoring by grouping is a useful process in algebra to help factor polynomials. This article describes this process. - Factoring: The Holy Grail of Algebra
Factoring and students often don't mix. This article shows a sure way to factor a trinomial provided it is factorable. - Logarithms: Help for a Great Algebra Mystery
This article takes the mystery out of logarithms and shows the algebra student already knows them.