Apollonius
Apollonius was born in Perga in southern Asia Minor in about 262 BC. He spent most of his life in Alexandria where he studied under the successors of Euclid; though he did spend a few years in Pergamum in western Asia Minor at a new university and library modelled on that at Alexandria.
Not much else is known about the life of Apollonius.
Apollonius is best remembered as one of the great mathematicians of antiquity. He was named ‘The Great Geometer’, mainly because of his work on conic sections. His greatest work, named Conics consisted of eight books and contained some 400 propositions. The eighth book is lost, but the other seven have been preserved. The first four are in Greek and expand on the work on conic sections of Euclid and other mathematicians; the other three have come down to us as ninth century Arabic translations and are more specialised.
Apollonius was also an astronomer. In contrast to the model Eudoxus proposed to represent the motion of the planets using concentric spheres, Apollonius proposed two alternative models called epicyclic motion and eccentric motion. In the epicyclic scheme, a planet was assumed to move uniformly about a small circle whose centre also moved uniformly around the circumference of a larger circle whose centre was the centre of the Earth. In the eccentric scheme, a planet was assumed to move uniformly about a large circle whose centre also moved uniformly around the circumference of a smaller circle whose centre was the centre of the Earth. These ideas led directly to the scheme for the motion of the planets later devised by Ptolemy.
Apollonius died in Alexandria around 200 BC.
A contribution of Apollonius to mathematics
Apollonius introduced the names ellipse, parabola and hyperbola for the three types of conic section, and obtained the conic sections from one circular double cone. If the double cone is cut by a plane, the curve formed by the intersection of the cone and the plane is called a conic section.
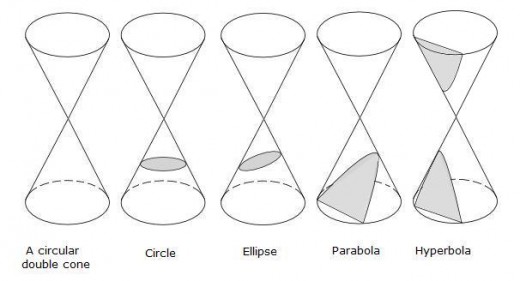
A circle is, of course, a special kind of ellipse, and is obtained by making a section through one cone parallel to the base of the cone.
Generally an ellipse is obtained by taking a section through the cone at a slight angle, and with all points on the curved face of the cone.
If the angle is increased so that the section goes through the base of the cone but with the vertex on the curved face of the cone and on the opposite side of the centre of the base of the cone, then we get a parabola.
If the angle is increased still further so that the section goes through the base of the cone and with the vertex on the curved face of the cone but on the same side of the centre of the base of the cone, then we get one branch of an hyperbola. The other branch is shown on the other half of the double cone.
Apollonius investigated the geometry of these conic sections and recorded them in his Conics . These ideas later formed the basis of the celestial mechanics of Kepler and Newton in the seventeenth century.