Michelson-Morley Experiment

The ether is the hypothetical medium that at one time was thought to support light waves. Many people feel that the Michelson-Morley experiment proved that the ether does not exit. However, this reasoning and calculations were based on the Galilean transformations (that is it did not allow for spatial contraction and time dilation). These calculations indicated that the time it would take for light to travel a distance in one direction and back would be different if the light traveled the same distance at 90^O to the first path. That is if the system were moving through the ether. The speed of light c = 3x10⁸ meters per second and the earth's speed in its orbit around the sun is about 0.01c. Therefore our speed through the ether must be at least 0.01c.

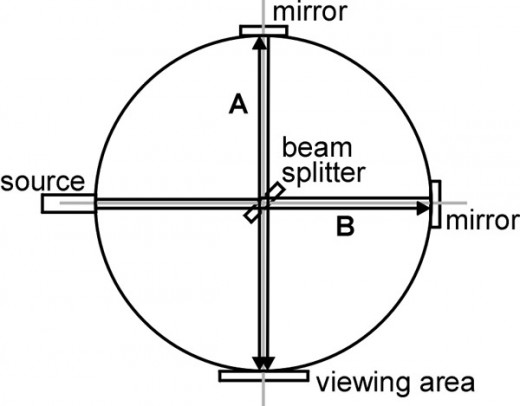
Figure 1 is a diagram of the device used in the Michelson-Morley experiment called an interferometer. A beam of light is emitted from a source on the left side of the diagram. This beam of light hits a beam splitter in the center of the diagram which divides it into two beams. One beam is reflected upward along arm A to a mirror at the top of the diagram which reflects it back to the beam splitter. The other beam is transmitted through the beam splitter along arm B to a mirror on the right side of the diagram, which reflects it back to the beam splitter. Part of both returning beams are combined by the beam splitter and travel down to a viewing area at the bottom of the diagram. If the distance that both beams travel along the arms A and B is the same then both beams will be in phase and cause a constructive interference pattern on the viewing area.* The circle represents all the possible positions that the ends of arms A & B could be rotated through

It was reasoned if this interferometer were moving to the right through the ether, the beam traveling along arm A would have to travel 2A/(1-v²/c²)^1/2 to make the round trip and the beam traveling along arm B would have to travel 2B/(1-v²/c²). This difference in time would cause the beams to be out of phase and create certain interference pattern. If the device were rotated, the distance that light must travel along each beam would change, thus causing the interference pattern to change. This could be easily seen if it occurred, but it never did, no matter the angle of rotation. The difference in the paths can be seen in figure 2. Here a speed of 0.6c was used for better separation in the illustrations.

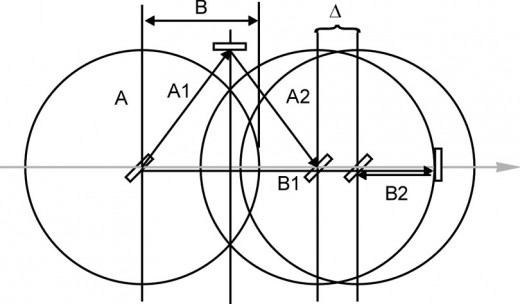
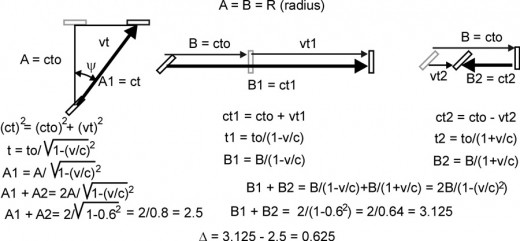
Fig. 3 shows the calculations (using the Galilean transformations) for an interferometer moving through space with a velocity of 0.6c. The time for light to travel the distance of the vertical arm A up and back down is 2.5 time units. The time for light to travel the distance of the horizontal arm B to the right and back to the left is 3.125 time units. The time difference Δ for light to travel the two differ paths is 0.625 time units.

For comparison, examine figure 4 and 5 which illustrates the interferometer moving through space with a velocity of 0.8c using the Lorentz transformations (that is allowing for spatial contraction and time dilation). The circle that represents all the possible positions, that the ends of arms A & B could be rotated through, is now contracted into the vertical ellipse (the spatial ellipse). Light strikes the beam splitter at the center of this ellipse and at that instant, starts its path along arms A & B. The large horizontal ellipse (the time ellipse) represents all the possible positions that the mirrors could have been rotated to, when the light strikes them. The term time ellipse is used because each part of the ellipse occurs at a different time as the light intercepts the circumference of the moving spatial ellipse.

The beam splitter is at the left focus of the time ellipse at the instant the light leaves it. The beam splitter is at the right focus of the time ellipse when the reflected light returns to the beam splitter. The sum of the distance from one focus to a point on the boundary of the time ellipse and the distance from that point to the other focus is a constant. This means no matter what the orientation if the interferometer to its motion through space, each light beam will always take the same amount of time to travel from the beam splitter to the mirrors and back again. This shows why the interference pattern in the Michelson-Morley experiment never changed no matter the orientation of the interferometer, even if the ether did exists. From this we see that the Michelson-Morley neither proved nor disproved the existence of the ether.

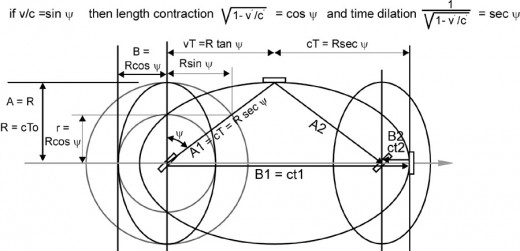
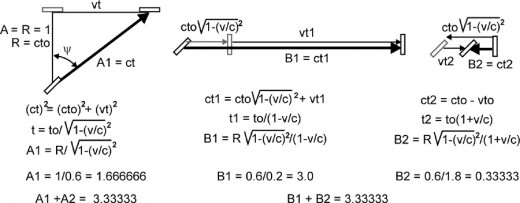
Fig. 5 shows the calculations (using the Lorentz transformations) for an interferometer moving through space with a velocity of 0.8c. The time for light to travel the distance of the vertical arm A up and back down and the time for light to travel the distance of the horizontal arm B to the right and back to the left are both the same. The two different paths that light travels are the focal radii of an ellipse. The ellipse is defined as the locus of points for which the sum of their distances (the focal radii) from two fixed points, the foci, is constant.

This repeated the Michelson-Morley experiment using unequal arms.* It was expected that even when taking the contraction hypothesis into account, one could expect a fringe shift on rotation of the interferometer because of the different lengths of the arms. No such shift was observed.

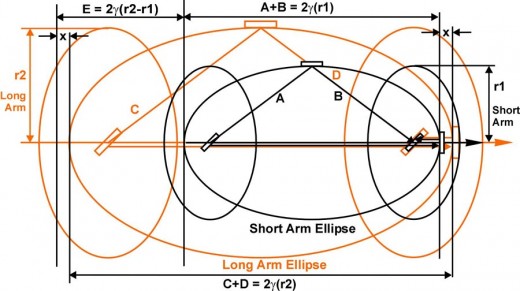
However, would unequal fixed arms cause a fringe shift on rotation of the interferometer? In fig. 6 the short arm ellipse is the locus of all the points where the light rays intercept all the possible positions of the mirror on the short arm rotated 360^O. The distance A + B is a constant 2γ(r1) regardless of the rotation the arm. The long arm ellipse is the locus of all the points where the light rays intercept all the possible positions of the mirror on the long arm rotated 360^O. The distance C + D is a constant 2γ(r2) regardless of the rotation the arm. The distance E, between the lengths of the two ellipses is a constant 2γ(r2-r1) regardless of the rotation the arm. In fig. 5-16, x is the offset between the front of long arm ellipse and the front of the short arm ellipse. The length of x = γ(1-v/c)(r2-r1).

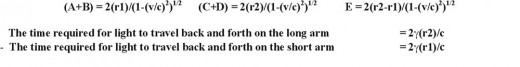
Since the time difference between the two paths is always a constant, the phase shift between the two beams should remain constant. Therefore, on rotation of the interferometer a fringe shift would not occur. Hence the Kennedy-Thorndike experiment neither proved nor disproved the existence the ether.

*Space-time Physics by Edwin F. Taylor & John A. Wheeler