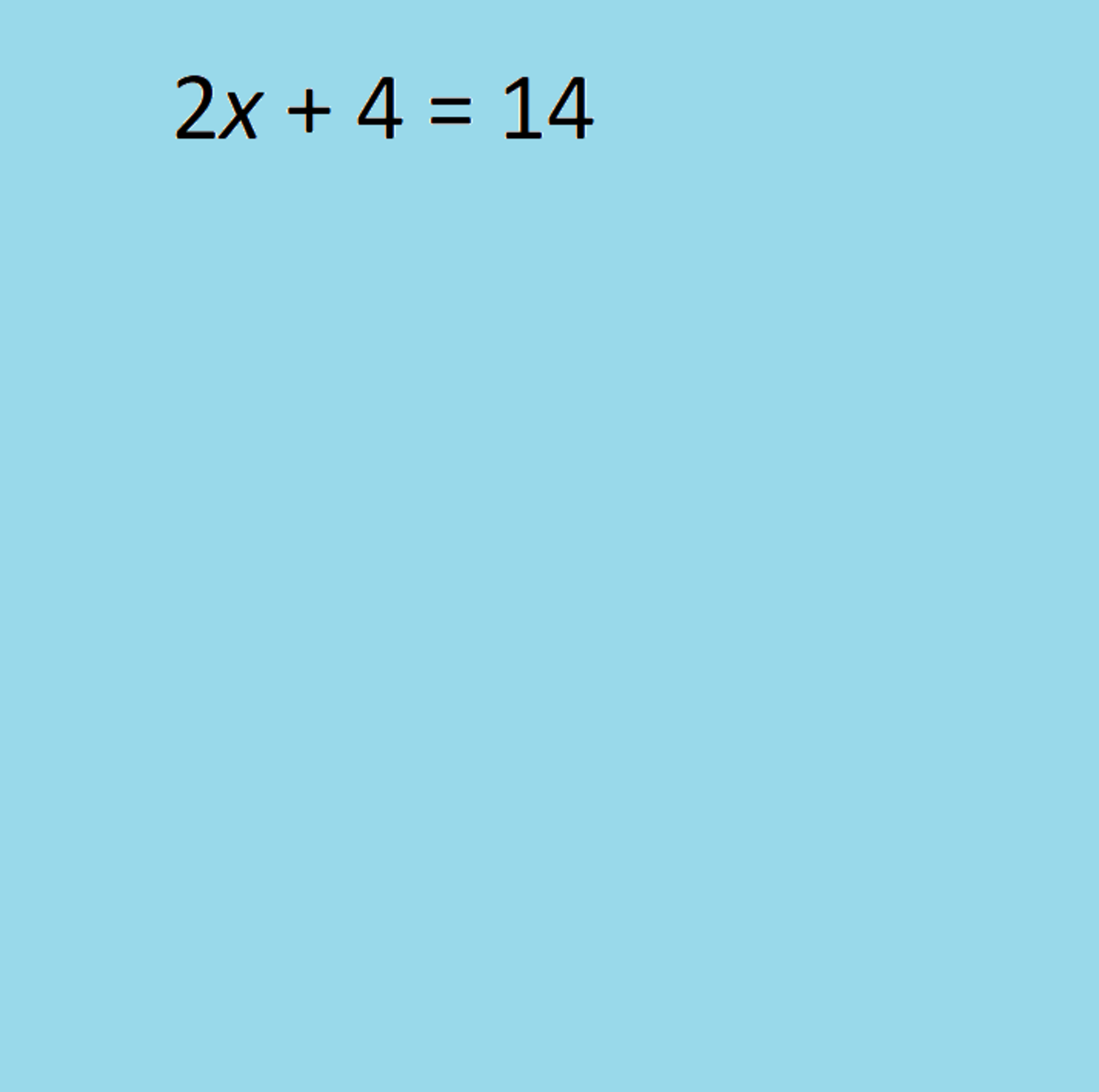More Help To Ace Your SAT Math Test, Tip #1
Now that I’ve introduced a critical strategy for increasing your SAT, ACT, GRE or GMAT math score – applying actual numbers – next I’d like to convince you to practice this strategy. In my test prep classes, I have to insist that students use this strategy in the assigned homework. Why? Because some of them will object that they know a faster way to solve it. Although there usually is a faster way to solve each math problem, the only way to get good at applying actual numbers is … well … to apply actual numbers! You don’t want to be trying it out for the first time on Test Day; you want this strategy to be a handy tool on Test Day.
Math problems may contain various features that determine how to apply actual numbers. Each of my next several hubs will discuss one of these features. I am using problems from the practice SAT test that the College Board currently has available on its website.
SAT Math Problem
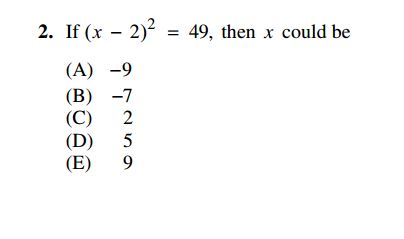
An Equation with a Single Variable
Of course! Math wizards, you most certainly can solve this one algebraically, and it would be faster. Go ahead! If you recognize that you can take the square root of both sides first, then you’ll make quick work of this one. If you FOIL it instead, well, you can get there from here:
x2 – 4x + 4 = 49
x2 – 4x – 45 = 0
(x – 9)(x + 5) = 0
et cetera
But even a problem as straightforward as this has lots of pitfalls – and the test writers pay attention to those pitfalls, and create answer choices accordingly. (Yep, they’re that mean.) For example, you’d could get answer choice (A) if you made a careless mistake on the first factor above. You might get answer choice (D) if you make a mistake with the value of x – 2, or answer choice (B) if you confuse x and x – 2.
Applying actual numbers on this problem is as easy as substituting the values of the answer choices into the equation:
(A) (-9 – 2)2 = 49 … but (-9 – 2)2 = 121, not 49, so cross off (A)
(B) (-7 – 2)2 = 49 … but (-7 – 2)2 = 81, not 49, so cross off (B)
(C) (2 – 2)2 = 49 … but (2 – 2)2 = 0, not 49, so cross off (C)
(D) (5 – 2)2 = 49 … but (5 – 2)2 = 9, not 49, so cross off (D)
(E) (9 – 2)2 = 49 … and (9 – 2)2 = 49, so select (E)
Could be ...
By the way, on this particular problem there’s a failsafe even if you make the silly mistake of thinking that -9 – 2 = -7. Notice that you’re asked which answer choice could be the value of x. For any “could be true” questions like this one, only one answer choice could possibly work out correctly. If at first you thought both (A) and (E) worked correctly, then you’d know for sure that you made a mistake – because this is a “could be true” question. I’ll have more tips about using question logic in a future hub.
The tip illustrated by this hub: When you see an equation with one variable, and the answer choices are actual numbers, then plug those numbers into the equation and see which one works.