More Help To Ace Your SAT Math Test, Tip #2

So far I’ve shown you my choice for the best way to improve your SAT math score – applying actual numbers – and I’ve shown how to use this technique in problems involving one variable. Let’s take the next logical step and look at problems that have an equation with more than one variable. In fact, let’s look at one of the ways in which the test writer’s make a problem look a little more complex – using f(x) instead of a simple variable like y.

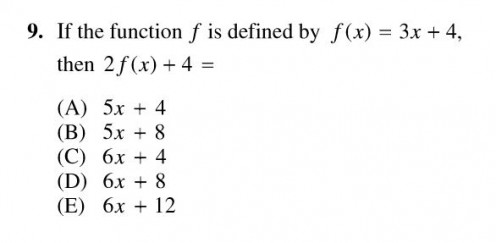
Seeing f(x) causes some test takers' eyes to glaze over. They mentally lapse back to that awful Algebra 2 class, where the teacher might as well have written out some problems with Greek. ( .... Oh, that’s right – she did!)

Not to worry! Although this may not work for every single function problem on a test like the SAT, often you can simply substitute y for f(x), and then handle the problem just like you would a two-variable problem:

With x and y instead of x and f(x), many test takers can now handle this problem algebraically, and I’ll give you an algebraic solution at the end of this hub. But for now I’ll do what I set out to do: give you another example of applying actual numbers.

As with the first problem I showed you when I introduced this strategy, the problem that we’re working on has variables in the answer choices. So we’ll pick numbers for the variables and find the answer to the question; apply the numbers we’ve picked to the answer choices; and select the answer choice that comes up with the same answer.

The one restriction when I pick numbers is that I must follow the rules in the question. In this case, the only rule is the equation y = 3x + 4. So I can’t just randomly pick a number for y and a number for x. Instead, I’ll pick a value for one of the variables and compute the value of the other variable. And the variable for which I’ll pick a number is the one that is NOT standing all by itself. That is, I’ll pick a value for x here, not for y. (If you think this through, you’ll see why: Suppose I pick y = 5. How do I compute the value for x? It’s a bit complicated! And furthermore, x is going to be some fraction. Ugh! Let me avoid fractions whenever I can!)

To keep the arithmetic easy, I’m going to pick a small number for x, though I won’t pick 0 or 1, because those numbers sometimes make the problem more difficult. So let’s go with the next easiest number – 2. If x = 2, then

y = 3(2) + 4 = 6 + 4 = 10

Now that I have a value for each variable, I will answer the question.

2f(x) + 4 = 2y + 4 = 2(10) + 4 = 24

The correct answer choice will give me a value of 24 when I plug in 2 for x:

(A) 5(2) + 4 = 10
(B) 5(2) + 8 = 14
(C) 6(2) + 4 = 16
(D) 6(2) + 8 = 20
(E) 6(2) + 12 = 24 ✓

To summarize: The feature to watch for is that the question includes an equation with more than one variable. The key to applying actual numbers is to pick a number for the variable that is NOT by itself, then compute the value of the other variable.

As promised, here is how I would solve this problem algebraically (still using y instead of f(x) for simplicity):

y = 3x + 4, so

2y + 4 = 2(3x + 4) + 4

(I’m betting that the test writer deliberately set this up with the repetitive “+ 4” just to see if anyone would think that the second one should be left off. That mistake would result in answer choice (D), by the way.)

2(3x + 4) + 4 = 6x + 8 + 4 = 6x + 12

Don’t forget – if you solve a problem algebraically, you can always check your work by applying numbers only to the answer choice you’ve selected.

And yes, this way is definitely faster. On Test Day, do it this way if you can. But when you’re practicing, apply actual numbers until you’re very familiar with this strategy.