How to Solve for Properties and Proofs of the Projection of Vectors for Calculus

Sometimes as we analyze vectors we are interested in finding out the individual components of a vector and where they are in relation to another but different vector. We may need to know how much each part points away from another vector and how much is along-side it. When we look at how much of a vector component is parallel to another vector, we are looking at the projection of that vector. Take a look at the following setup to see how this plays out.

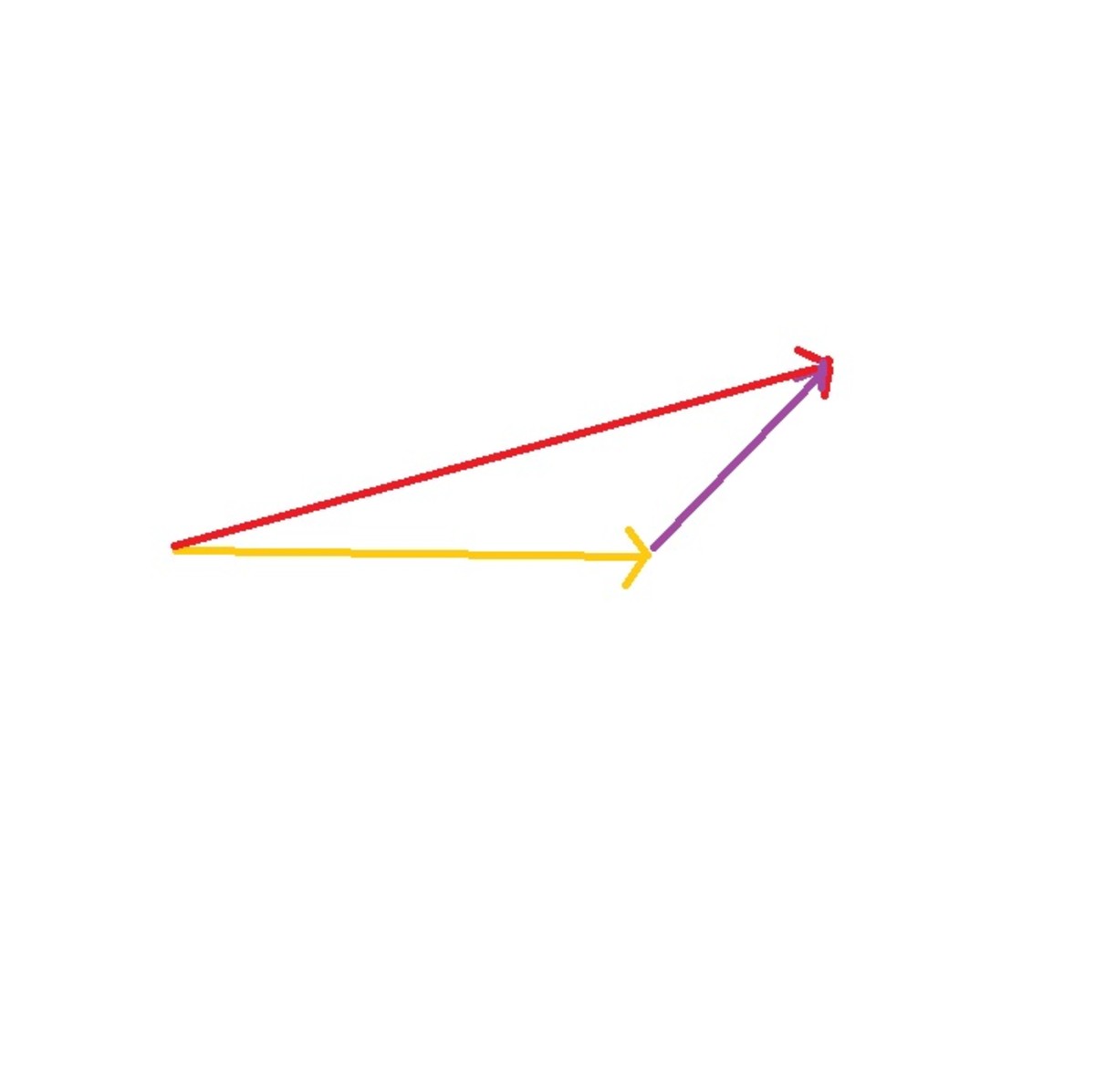
If I have two non-zero vectors a and b, I can break a down into the components c₁ and c₂ so that a = c₁ + c₂. These components are special because c₁ is parallel to b and c₂ is orthogonal to b. Because c₁ lies on b we say that it is the component of a onto b, or that the projection of a onto b is c₁. We notate this as

c₁ = proj_ab

And don’t forget, c₂ is orthogonal to b. It is also important to point out something you may observe as you use the projection. If the angle between the vectors is acute, then the projection points in the same direction as b and will seem to overlap portions of b, but if the angle between vectors is obtuse then the projection will point in the opposite direction as b and will not overlap it. The projection will still be parallel to b but the direction it points in depends on that angle, so tread carefully when confronted with this (Larson 785).

Now, it is great if you have the above information (knowing a, b, c₁, and c₂) because finding the projection is simply just extracting the correct information and inserting it into the proper equation. But what if you only knew a and b? How could you find that projection of a onto b without knowing those scalars or components? Well, note that c₁ has the length of c₁ (since it is just a component of a, the magnitude is just ||c₁|| = [(c₁)²]^0.5 = c₁) and it is in the direction of b. But to find a vector in that direction, I need to know the unit vector along that particular vector, in this case b. The unit vector in the direction of b would be b / ||b||. So,

c₁ = c₁(b/ ||b||)

But what does the c₁ equal? As previously mentioned, c₁ is a component of a. We need to use the angle between the vectors and basic trigonometry to find the component that is along b. Specifically,

c₁ = ||a||CosΘ

But CosΘ = (a ∙ b) / (||a||||b||), so

c₁ = ||a|| (a ∙ b) / (||a||||b||) = (a ∙ b) / ||b||

So, the projection of a onto b is

c₁ = [(a ∙ b) / ||b||] (b/ ||b||) = b (a ∙ b) / (||b||²) (786)

So now that we know what the projection of a onto b is, it may be insightful to observe the following:

c₁ = b (a ∙ b) / (||b||²) = [(a ∙ b)/||b||] (b/||b||) = k (b/||b||)

We can call k = (a ∙ b)/||b|| the component of a in the direction of b because the b/||b|| term is just a unit vector in the direction of b and k simply tells us the scalar amount of a that will end up being in that direction. It helps us see the underlining meaning behind many unusual terms and lots of jargon, which with calculus is very easy to get lost in. Knowing the meaning behind the equations is half the battle, truly (786).

If you are up for more calculus proofs, be sure to swing by my main website for even more!

Larson, Ron, Robert Hostetler, and Bruce H. Edwards. Calculus: Early Transcendental Functions. Maidenhead: McGraw-Hill Education, 2007. Print. 785-6.