Simple Harmonic Motion: Springs, Circuits, and Pendulums
Simple harmonic motion (SHM) is a type of oscillation in which the acceleration of the moving object is proportional to its displacement from a neutral position. It is the type of motion that is exhibited by a mass oscillating on a spring. Simple harmonic motion also appears in many other physical systems, such as swinging pendulums or electrical circuits.

Simple Harmonic Oscillator
The typical example of a simple harmonic oscillator is a system in which a mass is attached to one end of a spring, and the other end of the spring is fixed.
When the mass is pulled until it is a distance x from its original position, the spring stretches and a tension force acts on the mass. This force is:
F = -kx
where k is the spring constant and x is the size of the displacement. The minus sign is present because the force acts in the opposite direction to the displacement.
When the mass is released from a displacement x0, this force causes the mass to accelerate back towards its original position, according to the Newton's formula F = ma (force is mass times acceleration). However, because the mass continues to accelerate as it approaches its original neutral position, it overshoots its original position and the spring goes into compression. The compressed spring then exerts a force that decelerates the mass. The mass slows to a stop at a displacement of -x0, and the force acts to accelerate the mass back towards its original position. The mass continues to oscillate between positions x0 and -x0.
By equating the two expressions for F and writing the acceleration as
a = m d2x/dt2, we can write down a second-order differential equation which describes the motion:
d2x/dt2 = -(k/m)x
The solution to this equation is:
x = x0 cos(ωt), where ω=√(k/m) is the frequency of the oscillation and x0 is the initial displacement.
Each full oscillation takes 2π/ω seconds to complete.
Damped Simple Harmonic Motion
In the absence of friction, the mass on the spring would continue oscillating in this way for all eternity. However, in reality, energy is lost through frictional forces and the oscillation gradually decreases in amplitude until finally it stops altogether. This is known as damped simple harmonic motion:
Examples of Simple Harmonic Motion
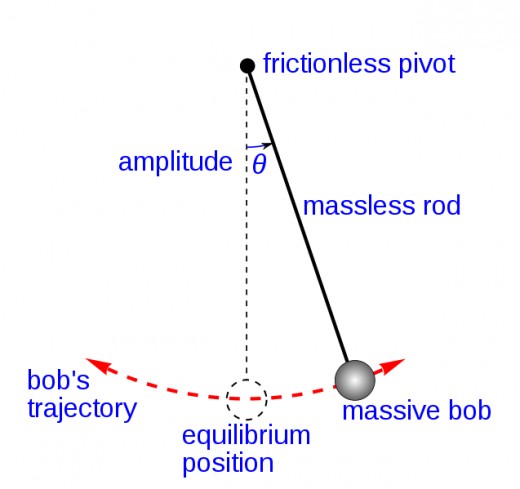
The motion of a swinging pendulum, for example in a grandfather clock, is approximately simple harmonic motion. The approximation holds providing the amplitude of the pendulum's swing is small.
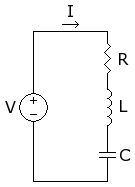
The flow of current in an electrical circuit containing a resistor, an inductor and a capacitor (an RLC circuit) is another example of simple harmonic motion. In this case, the voltage across the plates of the capacitor drives current to flow through the circuit. As the current flows through the inductor, a magnetic field builds up around it which keeps the current flowing even when the voltage across the capacitor has reduced to zero. The flow of current gradually builds up a voltage in the opposite direction across the capacitor plates. This voltage decelerates the flow of current and eventually reverses its direction. The current oscillates backwards and forwards, continually changing direction, just like the mass on the spring. Adding a resistor to the circuit introduces damping which eventually causes the oscillations to die away to nothing. These circuits are used in the tuning mechanisms of analogue radios.