Damped Simple Harmonic Motion

Damped simple harmonic motion is the real behaviour displayed by harmonic oscillators such as masses on springs, electrical circuits and pendulums.

Simple Harmonic Motion is an oscillating motion that occurs in systems where the force on the mass is proportional to its displacement from an equilibrium position - for example, a mass on a stretched spring or a pendulum. The equations of simple harmonic motion are beautifully simple. However, they are only an approximation to what happens in real physical systems. Real systems display damped simple harmonic motion. The damping - which causes the oscillation to slow down and stop - comes from frictional forces that occur in all real physical systems.

The equation that describes simple harmonic motion, in the absence of damping, is:

d²x/dt² = -(k/m)x

where k is the spring constant, x is the position of the mass m, and d²x/dt² is its acceleration. To learn more about this equation, see Simple Harmonic Motion.

The action of frictional forces (damping) can be included in the mathematical equation by adding in another term:

Frictional forces = -cv

The constant c is called the damping coefficient. This force is proportional to the velocity of the mass, and acts in the opposite direction to the mass' motion, which is why there is a minus sign in the expression. Once we add this term, the differential equation for damped SHM is:

m d²x/dt² = -k x – c dx/dt

It is nice to write this in the form:

d²x/dt² = - ω₀²x – 2ζω₀ dx/dt

where ω₀ = k/m is the oscillation frequency of the undamped oscillator.
ζ = c/(2mω₀) is called the damping ratio. The value of this damping ratio characterizes the behaviour of the system:

• If ζ > 1, the system returns to equilibrium without oscillating. This is called overdamping.
• If ζ = 1, the system returns to equilibrium, without oscillating, in the shortest possible time. This is called critical damping.
• If ζ < 1, the system oscillates for a while before returning to equilibrium. This is called underdamping.

You can prove these conditions by solving the equation to get an expression for x, which describes the motion of the oscillating mass:

x = x₀ exp(ζ ω₀ t) cos(ωt)

where ω = ω₀√( 1 – ζ² ) is the frequency of oscillation of the damped oscillator.

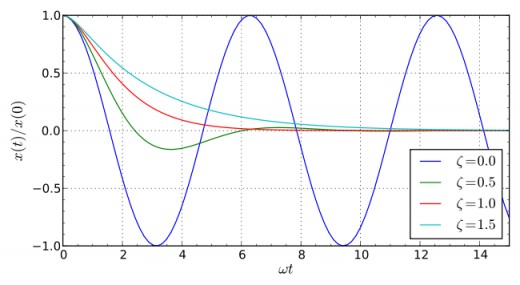
The solutions for the undamped, underdamped, critically damped and overdamped cases are plotted below. The undamped case (blue) continues oscillating. The underdamped case (green) oscillates once and then stops. The critically damped case (red) is the case in which the mass returns to equilibrium most quickly.

Damping is very useful in situations where oscillations are not desirable. For example, a door should be designed to swing shut and come to a gentle stop. To make this happen, the closing mechanism for the door must be critically damped. If the damping was too high, the door would take a long time to close, and if it were underdamped the door would slam shut quickly and ricochet noisily off the doorframe.

Electrical circuits in which the direction of the current oscillates according to simple harmonic motion (RLC circuits) are used as filters in electronics. An application for these circuits is in the tuning of an analogue radio. When the user turns the tuning knob, the capacitance of the circuit increases or decreases, so that the circuit's frequency of oscillation, ω, is increased or decreased. The circuit receives only receives radio waves that have a frequency close to ω. Therefore adjusting the capacitance of the circuit changes the station that the radio is tuned to.

The range of frequencies around ω that the radio can receive depends on the degree of damping. The higher the damping, the wider the range that will be received. For a radio to be usuable, the range of frequencies received must not be too high, or it would be receiving signals from more than one station at once. However, the damping in the circuit must be high enough that the system does not oscillate for too long after receiving the signal. The correct amount of damping can be selected by choosing the correct amount of resistance to include in the circuit.