Stellar Numbers (Part 1)

We are given the following diagrams which show a triangular pattern of evenly spaced dots. The numbers of dots in each diagram are examples of triangular numbers. (1,3,6,)…

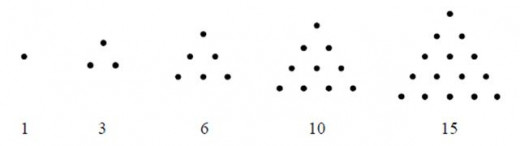
Looking at this triangular numbers we can link them to sequences where each triangle is sum of numbers. Next thing we can see is that every next triangle have one more row which is added to the previous triangle. This information which can be seen from these triangles can be put in table.

By using this table it is easier to work with data. So if each number of dots is sum of certain part of sequence we get that:

S₁=1; S₂=3, S₃=6, S₄=10, S₅=15

Since each number represent sum, we should find actual numbers in this sequence and from general formula for sum which says that: S_n=U₁+U₂ + U₃ + U₄ + … + U_n we can calculate these five numbers in this sequence: 1, 3, 6, 10, 15 and put them in table like it was shown above.

So; if S_n=U₁+U₂ + U₃ + U₄ + … + U_n then S₂=U₂+U₁ and since we have S₂ which is 3 and we know U₁ which is 1 we can calculate U₂; U₂= S₂ -U₁, we can therefore say that: U₂=3-1 so we can calculate this and U₂=2.

So; if S_n=U₁+U₂ + U₃+U₄+…+U_n then S₃=U₁+U₂+U₃ and since U₁+U₂=S₂ then S₃=S₂+U₃, so U₃=S₃-S₂ and from this U₃=6-3 we can calculate that U₃=3.

So; if S_n=U₁+U₂ + U₃+U₄+…+U_n then S₄=U₁+U₂+U₃+U₄ and since U₁+U₂+U₃ =S₃ then S₄=S₃+U₄, so U₄=S₄-S₃ and from this U₄=10-6 we can calculate that U₄=4.

So; if S_n=U₁+U₂ + U₃+U₄+…+U_n then S₅=U₁+U₂+U₃+U₄+U₅ and since U₁+U₂+U₃+U₄=S₄ then S₅=S₄+U₅, so U₅=S₅-S₄ and from this U₅=15-10 we can calculate that U₅=5.

From this information we can calculate difference in this sequence which can be determined by general formula which says d=U_n-U_n-1 and this formula is good only if sequence is arithmetic and difference is same between each number in sequence, this can be checked only by calculating three or more differences.

So, if we want to calculate difference between first and second number we take info from our earlier calculation and we get that U₂=2 and U₁=1 and then calculate d₁=2-1 and difference between first and second number is d₁=1.

If we want to prove that sequence is arithmetic we must calculate difference between second and third number so we take info from our earlier calculation and we get that U₃=3 and U₂=2 and then calculate d₂=3-2 and difference between first and second number is d₂=1. Since d₂ and d₁ are the same we can assume that this sequence is arithmetic but to be sure I will calculate d₃ and d_4.

Since d=U_n-U_n-1 then d₃=4-3 => d₃=1 and d₄=5-4 => d₄=1.

With these calculations we proved that this sequence is arithmetic and that the difference between each of them is 1. With this information we know that each new triangle has new row which is larger by one dot each time. And since this is typical arithmetic sequence we have general formula for sum of sequence terms which says that S_n= n/2 * (U₁+U_n) we can calculate how much dots have any triangle in this sequence.

For example if we want to calculate how many dots have the 15^th triangle in this sequence we will calculate it like this:

First of all we will find what is 15^th term in sequence and we will do that like this: U_n=U₁+(n-1)d so for the 15^th term in sequence is U₁₅=1+(15-1)·1 => U₁₅=1+14 => U₁₅=15 and then we use formula for S_n and calculate number of dots in 15^th triangle. So, calculation of S_n is like this: S₁₅= 15/2 · (1+15) => S_n= 15/2 · 14 => S_n=15 · 7 => S₁₅=105.

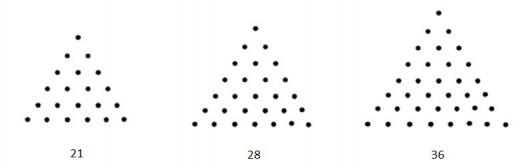
So with this we can easily draw the three more triangles and calculate how many dots they have:

So for the 6^th triangle we will calculate number of dots like this: Since U_n=U₁+(n-1)d we can calculate number of dots in new row: U₆=1+(6-1)1 => U₆=1+5 => U₆=6 and with this info we can calculate the number of dots in whole triangle. Hence S_n= n/2 ·(U₁+U_n) then S₆= 6/2 · (1+6) => S₆= 3 · 7 => S₆= 21.

For the 7^th triangle we will calculate number of dots like this: Since U_n=U₁+(n-1)d we can calculate number of dots in new row: U₇=1+(7-1)1 => U₇=1+6 => U₆=7 and with this info we can calculate the number of dots in whole triangle. Hence S_n= n/2 · (U₁+U_n) then S₇= ·(1+7) => S₇= 7/2 · 8 => S₇= 7 · 4 => S₇= 28.

For the 8^th triangle we will calculate number of dots like this: Since U_n=U₁+(n-1)d we can calculate number of dots in new row: U₈=1+(8-1)1 => U₈=1+7 => U₈=8 and with this info we can calculate the number of dots in whole triangle. Hence S_n= n/2 · (U₁+U_n) then S₈= 8/2 · (1+8) => S₈= 4 · 9 => S₈= 36.

Since we calculated number of dots in new row and the number of dots in whole triangle for next three triangles we can draw them: