Stellar Numbers (Part 2)

The next part of our task is to consider stellar (star) shapes with p vertices, leading to p-stellar numbers. The first four representations for a star with six vertices are shown in the four stages S1–S4 below. The 6-stellar number at each stage is the total number of dots in the diagram.

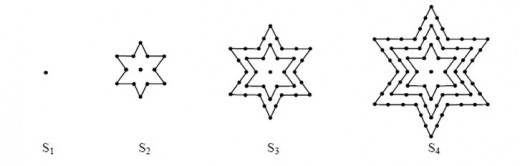
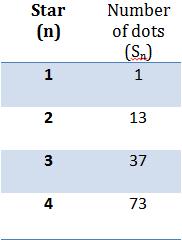
Again in this task like in previous one I will try to present this diagram in form of table because of easier work. I simply counted every dot in each star and put into the table.

Since each number represent sum, we should find actual numbers in this sequence and from general formula for sum which says that: S_n=U₁+U₂ + U₃ + U₄ + … + U_n we can calculate all numbers in this sequence.

So; if S_n=U₁+U₂ + U₃ + U₄ + … + U_n then S₂=U₂+U₁ and since we have S₂ which is 13 and we know U₁ which is 1 we can calculate U₂; U₂= S₂ -U₁, we can therefore say that: U₂=13-1 so we can calculate this and U₂=12.

So; if S_n=U₁+U₂ + U₃+U₄+…+U_n then S₃=U₁+U₂+U₃ and since U₁+U₂=S₂ then S₃=S₂+U₃, so U₃=S₃-S₂ and from this U₃=37-13 we can calculate that U₃=24.

So; if S_n=U₁+U₂ + U₃+U₄+…+U_n then S₄=U₁+U₂+U₃+U₄ and since U₁+U₂+U₃ =S₃ then S₄=S₃+U₄, so U₄=S₄-S₃ and from this U₄=73-37 we can calculate that U₄=36.

When we know this information then we can calculate the difference and check if the difference is the same each time. That can be easily checked by using this formula: d=U_n-U_n-1. This time I will calculate like this: U₃-U₂ = U₃-U₄ and if this is true then the difference is same for these two terms in this sequence.

So, by using U₃-U₂ = U₄-U₃ calculations go like this: U₃-U₂ = U₄-U₃ => 24-12 = 36-24 => 12 = 12 so the difference in both cases is twelve and because of this I will take this sequence partially arithmetic. I take it partially arithmetic because difference between second term and the first one isn’t 12 but because of the fact that after first term which is one in this case (that represents 1 dot) stars won’t get any additional points like this one in the middle I can work with other terms and take that part (after first term 1) of sequence as arithmetic.

Since we know what is the common difference in next terms we can calculate them in very simple way, by using this formula: U_n=U_n-1+d

So, since we need to calculate number of dots in each stage up to stage S₆ I will calculate U₅ and U₆ because I already have U_1to4. Using this simple formula I will calculate U_5. So, U₅=U₄+d => U₅ = 36+12 => U₅ = 48.

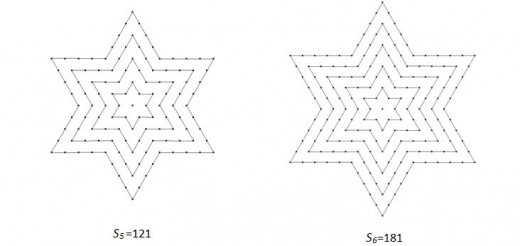
Before I calculate U₆ I can calculate how much dots is there in S_6. That can be calculated by adding the S₄ stage with number of dots in the next layer of star which is U_5. So, S₅= S₄+U₅ => S₅ = 73 + 48 => S₅ =121. This number S₅ shows how many dots is there in stage S₅ of the diagram.

Next thing I need to do is to calculate S₆ stage of the diagram and I should do that by calculating U₆ and then adding that number to the number of dots in stage S_5- So, U₆ = U₅ + d and by introducing our numbers into this formula we get U₆ = 48 + 12 => U₆ = 60. Now I need to calculate how many dots there is in stage S₆ of the diagram and that can be calculated by adding U₆ to the S_5. Hence U₆ = 60 and S₅ = 121 we can calculate that S₆ = 121 + 60 => S₆ = 181.

Now when I know how many dots are in new layer of star and how many dots are there in each stage I can easily draw those stars. They look like this: