The Lorentz Contraction, Or, How Motion Affects Space (Part 4 of 4)

In part 3, we discovered the mind-boggling distance, or space shortening phenomenon formally known as the Lorentz Contraction. This incredible property of nature can give rise to some very interesting situations, as we shall see in this last case. And therefore...

Let’s have a go at a final example, even though it’s once again an imaginary one. Imaginary, yes, but certainly conceivable, and furthermore, maybe even entertaining (albeit a bit cheesy). We envision that it is the year 2126, and that Scotty, due to his many technical improvements and innovations to the design of space cruisers while working as a Chief Engineer, has been promoted to the rank of Captain. Moreover, he has been given command of the CSS Avenger, the newest, sleekest, most state of the art, and just downright baddest space cruiser that has quickly become the pride of the Canadian space fleet. And so, our short story begins…

Avenger is currently cruising at flank speed relative to the space station CSP Alberta, as she is in the station’s immediate vicinity undergoing her final performance trials, when a frenzied distress call comes through to the station. “This is Captain Harmon of the CSS Defiant… We are under heavy attack from six Alpha Centaurian battle cruisers - repeat, six!… Caught us off-guard with their cloaking capability… Don’t have enough firepower to shake them off… We are totally defensive and sustaining major damage!… Shields holding but severely weakened – they won’t stay up much longer!… Our relative position is theta 21.553, delta 92.087, radius 1.500 from CSP Alberta… Alberta, please confirm our relative position using your sensors, then send the damned cavalry! We’re in deep sh*t!… Mayday, Mayday!”

Unfortunately, the cavalry consists of only one ship – the CSS Avenger, under the command of Captain Scott! All other fleet cruisers are currently on distant, deep space patrols. But Admiral Jackson, who is on board the space station Alberta, knows that the Defiant is in a grave situation, as she is being torn to shreds by Centaurian fusion torpedoes! Hence, he decides to cut the Avenger’s space trials short and send her directly into battle, in a desperate bid to rescue the Defiant. So Scotty, who is currently in his ship’s engineering control room carefully monitoring the performance of his matter/anti-matter reactors, hears his name boom over Avenger’s loudspeakers. “Commander Scott to the bridge, immediately! Commander Scott to the bridge, immediately! This is a code one ordinance!”

Scotty quickly arrives on Avenger’s bridge and plants himself into his captain’s chair. After being briefed about Defiant’s dire circumstances by his first officer, Scotty contacts his engineering control room without hesitation. “Captain Scott to Engineer Davis… Davy, what’s our ship’s current fuel status?”, to which his engineer calmly replies, “Captain, at our current flank speed of 0.943c relative to CSP Alberta, we’ve got enough anti-matter to buy us about 1 billion kilometers from the space station’s position, and then, we drift powerless after that, sir.” Scotty then hurriedly orders his navigator to ascertain the Defiant’s relative position. “Nav, contact CSP Alberta and get me a heading and distance to Defiant with respect to Alberta’s location.”. After quickly communicating with the space station, the discouraged navigator relays what she knows to be unfavourable information to Commander Scott. “Sir, Defiant’s position and distance are: Theta 21.553 degrees, delta 92.087 degrees, and distance 1.500 billion kilometers, relative to space station Alberta, as per the space station’s sensors’ readings.”

Avenger’s skipper pauses for a moment to compose his thoughts. He then orders his helmsman to head straight for the (already) nearby space station. Now, with his ship rapidly approaching the CSS Alberta, Scotty contacts Admiral Jackson in a frantic attempt to sequester extra fuel. “Captain Scott to Admiral Jackson… sir, we need much more fuel in order to reach Defiant! We’ll take all the anti-matter you can spare!”… “Avenger, this is Jackson. No anti-matter fuel to spare, and by the time we manufacture enough of the stuff, Harmon and his crew will have long been history! You’ll have to think of something else, Scott! Harmon can’t wait much more! His ship is being ripped apart! Jackson out.”, is the grim reply from the Admiral. At this point, Scotty knows there is nothing more that the Admiral can do, and so he reluctantly closes communications. “Something else? What the hell else can be done? We’ll come up way too short with the fuel we’ve got!”, thinks Scotty out loud.

Another short pause from the skip. And then, he slaps the side of his chair as his next thought comes to mind. “Short? Why, you sightless fool! The Lorentz Contraction is what will get us to Defiant on the fuel we’ve got! Thank you, special relativity!”. Scotty then makes some quick calculations using the ship’s computers, and then immediately converses with his engineer.

[ Scott: ] “Davy, heads up – Defiant is 1.5 billion kilometers from the space station, as measured by the space station’s sensors. She’s being ripped to shreds by enemy ships as we speak, so we’ve got to get to her, ASAP! Now our ship is currently moving at a speed of 0.943c relative to the space station; but essentially, relative to the Defiant also, because she is basically drifting powerless in space at an extremely slow speed RELATIVE TO the Alberta, and is therefore virtually AT REST with respect to the space station. So here’s my question, Davy, and you’d better give me the answer I want, or you’re fired!... Can we maintain our relative speed of 0.943c until we close in on Captain Harmon’s ship?”

[ Davis: ] “This is a mighty dangerous relative speed to maintain, Captain. It’s only meant for our performance trials, sir. Holding this speed for any extended period of time might just rip us to shreds! And besides, we’ve only enough anti-matter for 1 billion kilometers, sir. Defiant is way out of our maximum range!”

[ Scott: ] “No she isn’t, Mister Davis. Not if my calculations are accurate!”

[ Davis: ] “Beggin’ your pardon, Captain, but what exactly are you getting at, sir? There’s just no way we can save that ship! She is just way out of our fuel range, sir! 500 million extra kilometers outside our range, to be exact, Captain!”

[ Scott: ] “Listen, Davy, here are my calculations. Okay… recall your special relativity. Let’s say we maintain our ship’s relative speed, that is, our ship’s speed relative to BOTH the space station AND the Defiant, at 0.943c . Now if we make a direct, straight course from the space station’s position to Defiant’s position while maintaining this speed, then from OUR point of view, the equations of special relativity show that the distance itself between the space station and the Defiant will contract by a factor of 3! That will literally shorten the normal distance of 1.5 billion kilometers as measured from ALBERTA’S point of view, to only 500 million kilometers, as measured from OUR point of view! And since we’ve got enough fuel for 1 billion kilometers, we should have plenty left over to shove our boots up the Alpha Centaurians’ asses and tow Defiant to safety! It’s the mechanics of relativistic distance contraction, Mister Davis!... We can consider our ship to be at rest while the space station, the Defiant, and the distance between them are the ones that are moving at 0.943c relative to us instead! And so the distance contraction phenomenon will, from our point of view, cause the normal 1.5 billion kilometers between Alberta and Defiant to shrink by a factor of 3, enabling this ship to get to Defiant using much less fuel than what we already have in our tanks!... Davy, I need you to verify my calculations within the next minute. This vessel has got to maneuver, and that means now! That’s a direct order, mister! And if it means that this ship flies apart, well… we’ll fly her apart, then! Captain out.”

[ Davis: ] “Aye Aye, sir – right away!”

Engineer Davis immediately turns to the ship’s computers to quickly validate Scotty’s calculations.

[ Davis: ] “Computer… normal distance from Alberta to Defiant, L₀, equals 1.5 x 10⁹ kilometers. Speed of travel relative to Alberta and Defiant equals 0.943c. Calculate contracted distance, L_C, from Alberta to Defiant, distance contraction factor, and remaining fuel upon reaching Defiant. This is a category one directive from Lieutenant Commander Montgomery Davis, CSS Avenger. Execute immediately.”

[ Davis: ] “Engineering to Captain Scott… that ties it! The haggis is in the fire for sure, sir! Because of relativistic distance contraction, once we reach Defiant’s position, we’ll have enough fuel remaining to give those scum sucking Centaurians the can of kick ass they deserve, and then tow Captain Harmon and his crew to safety! Davis out.”

[ Scott: ] “Excellent, Mr. Davis. Helmsman, we’re rapidly approaching the space station’s position. Maintain our relative speed of 0.943c until further orders. Once we reach the space station’s position, make a straight course to directly intercept the Defiant. Weapons officer, all deflector shields to maximum power. Make ready all hyper intensity lasers and matter/anti-matter torpedoes. We’ll be going into battle shortly – this is not a drill! Condition status is red. Sound general quarters!… Captain Scott to Admiral Jackson… the cavalry is on its way, sir! Yipee – Cayay! Scott out.”

And with that final cowboyish sign-off from Captain Scott, the CSS Avenger, with every bolt and rivet barely holding the ship together as she thunders towards Defiant, makes good on her promise to send the Alpha Centaurian battle cruisers limping back to their home star system, and to rescue CSS Defiant and her brave crew. This rescue mission was first thought to be impossible due to Avenger’s lack of fuel, but was made possible, using the ship’s existing fuel supply, by the distance contraction phenomenon of the special theory of relativity, formally known as the Lorentz Contraction! ^[7]

But we might now be wondering to ourselves, “What does the Avenger’s journey – from the space station Alberta to the battleground of the space cruiser Defiant – 'look like', from the point of view of Admiral Jackson, who is observing things unfold from the comfort and safety of the space station?”. Well, for starters, from Jackson’s point of view, the CSP Alberta and the CSS Defiant are essentially at rest relative to each other. Thus, from Jackson’s perspective, that is to say, as measured by Jackson’s rulers, the Alberta and the Defiant will always be separated by the normal distance of 1.5 billion kilometers. And furthermore, from Jackson’s point of view, it is obviously the CSS Avenger, commanded by Captain Scott, that is moving at the speed of 0.943c relative to the space station and the Defiant. Therefore, due to the relativistic length contraction and relativistic time dilation phenomena, not only will Admiral Jackson observe the Avenger herself to be 3 TIMES shorter than her normal length, but he will also observe Avenger’s clocks to be ticking 3 TIMES slower than his space station’s clocks, which are of course, from Jackson’s point of view, ticking at the normal rate of time passage. Hence, this slowing down of time – by the factor of 3 – aboard the Avenger as observed by Jackson, will lead the noble Admiral to conclude that the space cruiser is therefore consuming its fuel 3 times slower than it normally does. Consequently, Jackson will observe the Avenger traverse the entire normal distance – from his space station to the Defiant – of 1.5 billion kilometers, but he will observe Avenger consume only 500 million kilometers worth of fuel to get there (specifically, 1.5 billion km / 3 = 500 million km worth of fuel), which is in complete agreement with Captain Scott’s and Engineer Davis’ observations! And hence we see, once again, that relativistic distance contraction and time dilation are “two sides of the same coin”. From the viewpoint of Captain Scott, it is distance contraction that allows his ship to save fuel and reach the Defiant, while from the viewpoint of Admiral Jackson, it is time dilation that allows the Avenger to save (the same amount of ) fuel and reach the Defiant!

In this discussion, we have derived the relativistic distance contraction factor using special relativity’s two fundamental postulates. The following scenario will demonstrate, nonetheless, that the distance contraction factor can be derived in an equivalent manner, using what we already know about the time dilation phenomenon.

(1) We imagine that we are standing idly by on our train station platform, expecting that Scotty’s locomotive will very soon be rumbling through, say, from left to right, at the speed v relative to us (but he ain’t stoppin’, ’cause he knows that we’re here, and resents the fact that we called him a ‘loud mouth’ earlier on in our discussion – the fool).

(2) Now let’s also say that the normal length of our train station platform, namely, its length as measured by us using our tape measure (i.e., while WE are therefore AT REST relative to the platform), is L₀.

(3) But Scotty, who has delusions of grandeur, also wants to measure the length of the platform because he wants to build a lavish train station of his own, to cater exclusively to his snobby, stuck-up, “VIP” passengers. Since he’s not stopping, however, he’ll have to use an indirect method to obtain the platform’s length, and this is how he’ll do it: Scotty will start his stopwatch as soon as the leftmost edge of the platform coincides with the frontmost point of his locomotive, and then stop his stopwatch as soon as the rightmost edge of the platform coincides with the frontmost point of his locomotive. Let’s call this time interval that is recorded on Scotty’s stopwatch Δt_SCOTTY (at this point, we quickly remind ourselves that our platform, which, when observed from Scotty’s point of view, is the one that’s moving at the relative speed v instead). Scotty can then use the relationship that

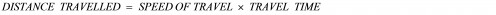
to calculate the length of our platform, which we’ll call L_SCOTTY, for himself. Hence, it is clear that

(4) From our point of view, on the other hand, since it is Scotty’s locomotive that is moving at the relative speed v, then due to the time dilation phenomenon, we will observe Scotty’s stopwatch ticking at a slower rate than the normal rate of time passage. Therefore, as a direct consequence of Scotty’s more slowly ticking stopwatch, its recorded time interval, Δt_SCOTTY, will be less than normal, leading us to realize that Scotty’s indirect method for calculating our platform’s length will give him a result that is shorter than its normal length, L₀. Hence, Scotty will observe our platform to be contracted, or shortened, along its length, in accordance with the Lorentz Contraction. This result agrees with our first formal conclusion about the distance contraction phenomenon, which states that “An object that is in RELATIVE UNIFORM MOTION, that is to say, an object that is moving in a STRAIGHT LINE and at a CONSTANT SPEED relative to an observer, will appear, to the observer, to be CONTRACTED, or SHORTENED from its normal length, ALONG THE DIRECTION OF RELATIVE MOTION.” In our current example, of course, the observer is Scotty, and the object in (relative) motion is our platform.

(5) But we have also already established that the platform’s contracted length that Scotty will (indirectly) measure, must be contracted, with respect to the platform’s normal length, by the relativistic distance contraction factor

such that

So the question is, how can we logically ‘reproduce’ this equation using the facts of our current scenario? Enter the time dilation phenomenon once again. Since our train platform’s clocks are obviously at rest relative to us, then we will observe them to be ticking at the normal rate of time passage, specifically, we will observe Scotty’s relatively moving stopwatch to be ticking more slowly than our relatively stationary platform clocks. Thus, AS OBSERVED FROM OUR POINT OF VIEW, that is to say, as measured by US using OUR platform clocks, the normal amount of time that it will take (the frontmost point of) Scotty’s locomotive to travel the entire normal length of our train station platform must be equal to

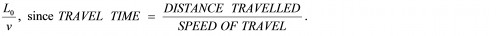
Therefore, the corresponding time interval Δt_SCOTTY must be less than this normal time interval L₀ / v, because we observe Scotty’s stopwatch ticking more slowly than our platform clocks. Furthermore, from our discussion on time dilation, we know that Δt_SCOTTY must be less than L₀ / v in a very specific way; in a way such that

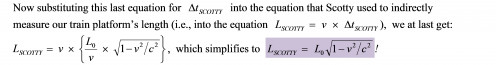
Therefore, we have arrived at the original equation for the Lorentz Contraction, which, in essence, is saying that: The platform’s contracted length, L_SCOTTY, that Scotty will observe, must be contracted, with respect to the platform’s normal length, L₀, by the relativistic distance contraction factor sqrt(1 - v² / c²).

Hence, we have demonstrated the fact that Scotty measuring a shortened length for our train station platform is a direct result of the fact that his clocks were ticking at a slower rate than the normal rate of time passage, that is to say, the distance contraction phenomenon is a direct result of the time dilation phenomenon.

Okay. Now imagine that the situation is reversed, so that we are trying to measure the length of Scotty’s relatively moving locomotive, using this indirect method. We start our platform clock as soon as the frontmost point of the locomotive coincides with the midway point of our platform, and then stop our platform clock as soon as the rearmost point of the locomotive coincides with the midway point of our platform. We can then calculate the locomotive’s length by multiplying its relative speed, v, by the time interval that has elapsed on our platform clock. From Scotty’s point of view, however, it is our platform that is moving at the relative speed v, and due to the time dilation phenomenon, Scotty will observe our platform clock ticking at a slower rate than the normal rate of time passage. Therefore, as a direct consequence of our more slowly ticking platform clock, its recorded time interval will be less than normal, leading Scotty to realize that our indirect method for calculating his locomotive’s length will give us a result that is shorter than its normal length. Moreover, if we repeat the physics and math logic of our current example (let’s take that as a challenge!), then we will find that the locomotive’s contracted length that we will observe, must be contracted, with respect to the locomotive’s normal length, by the relativistic distance contraction factor sqrt(1 - v² / c²) also!

Now, we might be wondering, “Why is contraction limited only to distances along the direction of motion, that is, why don’t distances perpendicular to the direction of motion contract also?”. A rational question, with the answer being that if distances indeed contracted in directions perpendicular to the direction of motion, then we would eventually come face to face with a true logical and physical contradiction. Let’s imagine that Scotty’s train is rumbling towards a circularly shaped tunnel entrance at close to the speed of light. From Scotty’s point of view, he is at rest, and it is the tunnel entrance that is moving towards his train at close to light speed instead. Hence, if perpendicular distances did indeed contract, then from Scotty’s perspective, the diameter of the moving tunnel entrance (which is perpendicular to the direction of motion) would therefore decrease. In fact, if the relative speed was great enough, Scotty would see the tunnel entrance decreased in diameter such that his train would no longer fit through. Thus, from Scotty’s perspective, the side of the mountain would slam into his train, flattening him into a pancake and killing him instantly!

From the tunnel entrance’s point of view, however, it’s a completely different story. From the entrance’s perspective, it is at rest, and Scotty’s train is moving towards it instead. And again, if perpendicular distances did indeed contract, then the tunnel entrance would “see” both the height and width of Scotty’s train (which are perpendicular to the direction of motion) decrease. But since the cross section of the train would only become smaller and smaller as the relative speed increased, then it would obviously always be able to fit through the tunnel entrance no matter what the speed, from the entrance’s point of view!

Therefore, from Scotty’s viewpoint, there would exist a relative speed at which his train would no longer fit through the tunnel entrance, but from the entrance’s viewpoint, the train would always fit through, regardless of how great the relative speed became, thus resulting in a logical and physical contradiction. And so, as a consequence of this true paradox, we can conclude that distances that are perpendicular to the direction of relative motion do not, and cannot, contract or shorten whatsoever, and thus remain unchanged. ^[8]

We may be wondering why this astounding phenomenon is called the “Lorentz Contraction”, and not the “Einstein contraction”. The reason is that it was the great Dutch physicist, H.A. Lorentz, who first theorized that distances shorten in the direction of motion. He made this hypothesis in order to explain the negative results of experiments – the most famous being that performed by A. Michelson and E. Morley in 1887 – that were specifically designed to determine the earth’s absolute velocity through space (which we now know, does not exist), by measuring the expected time difference between the paths of light pulses reflecting between two pairs of mirrors. One pair was positioned along the earth’s direction of motion around the sun, and the other was positioned perpendicularly to it, in the exact manner that one of the photon clocks in our thought experiment was positioned along the train’s direction of motion, and the other was positioned perpendicularly to it, for which we calculated the times t_H and t_V, respectively. And just as we wrongly expected a difference between these times, so too did the physicists wrongly expect a time difference between the paths of the light pulses. It was Lorentz’s contraction hypothesis that accounted for the fact that there were no time differences detected by any of these experiments whatsoever (in the exact manner that we discovered that Clock H had to contract in length so that t_H = t_V !). However, unlike Einstein, Lorentz still held on to the notion of absolute time (and absolute motion). But who could blame him? The concept that time flows at the same rate for all things, that there is one and only one “master clock” that ticks away the durations between all the happenings in the universe, is extremely logical and makes excellent common sense. It was Albert Einstein, essentially using only his two very potent fundamental postulates and his many “thought” experiments (a few of which we have borrowed), who threw out these “deeply rooted prejudices” – with great difficulty of his own – and deduced that the rate at which time passes is not the same for everyone, but rather, varies depending on one’s relative speed. And as we have seen by way of examining the curious case of the cosmic muons, the direct consequence of relative time is relative space. Hence, Einstein also fused space and time together, from existing as two separate, independent entities, to existing as one interwoven fabric known in physics today as “spacetime”. As Hermann Minkowski, who was the Big E.’s former mathematics professor, summed it up:

“… Henceforth space by itself, and time by itself, are doomed to fade away into mere shadows, and only a kind of union of the two will preserve an independent reality.”

[7] In reality, the fuel consumption calculations are much more complex than those used in the example. For one thing, the ship must first accelerate to its cruising (relative) speed by applying thrust (during which period, fuel is consumed); then coast at this speed for the majority of its journey (during which period, virtually no fuel is consumed); and finally decelerate by applying reverse thrust (during which period, fuel is again consumed), so that the ship doesn’t overshoot its destination. The example’s main purpose is to further illustrate the Lorentz Contraction, and to show, once again, that time dilation and distance contraction are not mutually exclusive phenomena.

[8] We might still be wondering, however, “Instead of contraction along the direction of motion, why not expansion in the direction perpendicular to it? That is, instead of Clock H contracting in length, hence decreasing the amount of time t_H until t_H = t_V and thereby keeping itself in sync with Clock V, why couldn’t Clock V expand in height instead, hence increasing the amount of time t_V until t_V = t_H, thereby still keeping both clocks in sync? Specifically, why don’t distances perpendicular to the direction of motion expand instead, so that the first postulate (i.e., the principle of relativity) is still upheld ?”. Another rational question, with the answer being the same as before – that if distances indeed expanded in directions perpendicular to the direction of motion, then we would again eventually come face to face with another true logical and physical contradiction. Let’s imagine, once more, that Scotty’s train is rumbling towards the same circularly shaped tunnel entrance at close to the speed of light. From Scotty’s point of view, he is at rest, and it is the tunnel entrance that is moving towards his train at close to light speed instead. Hence, if perpendicular distances did indeed expand, then from Scotty’s perspective, the diameter of the moving tunnel entrance (which is perpendicular to the direction of motion) would therefore increase. But since the tunnel entrance would only become larger and larger as the relative speed increased, then Scotty’s train would obviously always be able to fit through the tunnel entrance no matter what the speed, from Scotty’s point of view.

From the tunnel entrance’s point of view, however, it’s a completely different story once more. From the entrance’s perspective, it is at rest, and Scotty’s train is moving towards it instead. And again, if perpendicular distances did indeed expand, then the tunnel entrance would “see” both the height and width of Scotty’s train (which are perpendicular to the direction of motion) increase. In fact, if the relative speed was great enough, the tunnel entrance would “see” Scotty’s train increased in height and width such that the train would no longer fit through, and thus, from the entrance’s perspective, the train would slam into the side of the mountain, thereby pulverizing Scotty into soot and killing him instantly yet again!

Therefore, from Scotty’s viewpoint, his train would always fit through, regardless of how great the relative speed became. But from the entrance’s viewpoint, there would exist a relative speed at which the train would no longer fit through the tunnel entrance, thus resulting in a logical and physical contradiction for a second time. Therefore, as a consequence of this true paradox, we can once again conclude that distances that are perpendicular to the direction of relative motion do not, and cannot, expand or lengthen whatsoever, and thus remain unchanged.