The Lorentz Contraction, or, How Motion Affects Space (Part 3)

In Part 2, we were able to deduce, using only special relativity's two fundamental postulates, that as observed from our point of view, Scotty's (relatively) moving Photon Clock H must indeed contract in length, that is to say, contract along the direction of relative motion by a factor of sqrt(1 - v² / c²), in order to keep its original synchronization with his Photon Clock V and thus uphold the principle of relativity. We will now discuss some consequences of this astonishing distance contraction phenomenon, formally known as the Lorentz Contraction.

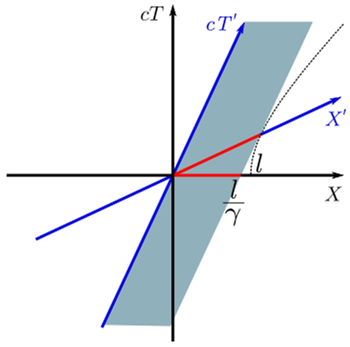
We had initially believed that from our point view, we would observe Scotty’s Clock H fall out of sync with his Clock V, because of our erroneous prediction that t_H > t_V. But we need not be too harsh on ourselves, for this error was a direct result of our (very rational, reasonable, and SANE) assumption that Clock H’s length would remain unchanged by the relative motion of Scotty’s train, as observed from our perspective! But, contrary to our flawed assumption, we must instead face the reality that: From our point of view standing at the train crossing, we will observe Scotty’s Photon Clock H to be contracted, or shortened, along the horizontal direction, that is, along the direction of his train’s relative motion. Thus, as his T.O. Special thunders through the crossing at the speed v relative to us, we will observe that

where h_C is the contracted, or shortened length of his Photon Clock H, as shown in Figure 1.3, and h is its normal length, as shown in Figure 1.2. And this necessary amount of shortening of Clock H’s length will ensure that t_H = t_V and NOT t_H > t_V, as measured by us using our watches, thus keeping Clock H in synchronization with Clock V as observed from our point of view, for ANY relative speed v, and hence upholding the first postulate, that is, the principle of relativity.

Stating it less formally, one final time: Because of his train’s motion relative to us, then as seen from our perspective, Scotty’s Clock H will become shorter than its original, that is, its normal length in the horizontal direction by the factor

so that the total distance that its photon must travel to complete 1 tick is decreased to the same total distance that Clock V’s photon must travel to complete 1 tick. And this shortening of the length of Clock H will therefore keep both clocks, as observed from our point of view, in sync with each other, as they must be. Figures 1.1, 1.2, and 1.3 comprise a clear and concise summary of Einstein’s logic behind this truly astounding result.

Moreover, since there is absolutely nothing special, magical, or supernaturally spooky about Scotty’s photon Clock H – heck, at the end of the day, it’s just two ordinary mirrors mounted onto a metal shaft; and besides, Clock H’s mirrors can’t even tell the wicked stepmother just what a hideous, butt-ugly warthog she truly is – then we are forced to conclude that as observed from our point of view, all objects, living or inanimate, that are aboard the relatively moving train, and of course the train itself, must also shorten by the same factor sqrt(1 - v² / c²) along the direction of the train’s relative motion! Hence Scotty, if he is standing up, will appear to us, along with his vertically positioned photon Clock V and all other ‘vertically’ positioned objects, to be thinner than normal. On the other hand, those passengers who are lying down along the direction of the train’s relative motion and snoozing will appear to us, along with their bunk beds and all other objects positioned ‘horizontally’ along the direction of relative motion, to be shorter than normal! And the entire train itself must, of course, also contract and become shorter than its normal length!

So, our first formal conclusion is that: An object that is in RELATIVE UNIFORM MOTION, that is to say, an object that is moving in a STRAIGHT LINE and at a CONSTANT SPEED relative to an observer, will appear, to the observer, to be CONTRACTED, or SHORTENED from its normal length by the factor sqrt(1 - v² / c²) ALONG THE DIRECTION OF RELATIVE MOTION, where v is the SPEED OF THE OBJECT RELATIVE TO THE OBSERVER, and c is the universally constant SPEED OF LIGHT. We shall call this factor, namely, sqrt(1 - v² / c²), the “(relativistic) distance contraction factor”.

Therefore, if L₀ is the normal length of a straight rod that is moving at a speed v relative to an observer, then the observer will measure the rod to be contracted, or shortened, to a length L_C, where

provided that the rod lies along the direction of relative motion, that is to say, provided that the rod is pointing in the direction of relative motion. If the observer, however, is instead moving with the rod, so that the rod is at rest relative to the observer, then of course, the observer will not see the rod to be contracted whatsoever, and will therefore measure the length of the rod to be just its normal length, L₀. Let’s take this scenario a small step further. If the rod and the observer are still at rest relative to each other, but are now both moving at a speed v relative to us, then we already know that we will measure the rod to be contracted to a length of L_C = L₀ x sqrt(1 - v² / c²) along the direction of relative motion (not to mention the observer, who will also appear contracted by the same factor). Nothing new, yet. If, however, we ‘watch’ the observer as she again measures the length of the rod for herself using her ruler, then we will ‘see’ that, from her point of view, she will still measure the length of the rod to be just its normal length, L₀, BECAUSE, as viewed from our perspective, her ruler will also be contracted by the factor sqrt(1 - v² / c²) !

And let’s not forget our second formal conclusion, which states that: The GREATER the relative speed, v, of the moving object, the GREATER the amount of CONTRACTION of the object along the direction of relative motion.

And why is this the case? Because, mathematically speaking, as v becomes greater and greater and approaches the speed of light, c, the value of the quantity v² / c² gets closer and closer to a value of one, and hence the value of the relativistic distance contraction factor, sqrt(1 - v² / c²), becomes less and less, and approaches a value of zero. Putting it into some symbols to obtain a clear depiction of our logic, we get:

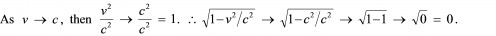
Consequently, distances get shorter and shorter along the direction of motion, and in fact approach zero length as v approaches the speed of light c! Stating things in a more ‘pictorial’ way, if Scotty’s train travels faster and faster, then a GREATER AND GREATER DIFFERENCE would BUILD UP between the TOTAL DISTANCES that Clock H’s and Clock V’s photons would need to travel to complete their respective ticks, as ‘seen’ from the observer’s point of view, HAD CLOCK H NOT SHORTENED TO BEGIN WITH! Therefore, a shorter and shorter Clock H, as ‘seen’ from the observer’s perspective, can OFFSET, or “CANCEL OUT” this ever increasing difference between the total distances, and in this manner, Clock H can keep itself in sync with Clock V at any and all relative speeds, as required by the first postulate! ^[6]

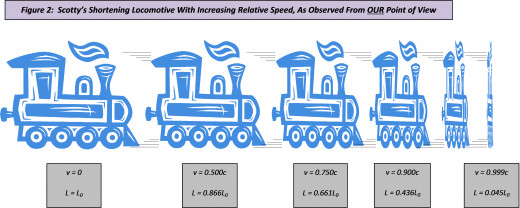
Let’s work out a few examples whose scenarios have become very familiar to us by now, to best illustrate this truly extraordinary phenomenon. First up is Scotty’s train, as it blazed through the crossing at the relative speed of 0.866c. From our point of view, not only did we observe that his clocks were running 2 times slower than ours (i.e., 2 times slower than normal), but we also observed that the length of his train was 2 times shorter than its normal length, that is to say, its normal length was contracted by the factor 0.5 in the direction of relative motion. So let’s put our formula to the test. If we let L₀ equal the train’s normal length and L_C equal its contracted length, then our formula tells us that:

Specifically, if we took our rulers and measured the length of Scotty’s locomotive while it was still at the train station, that is, while his locomotive was still at rest relative to us, so that there could be no length contraction (nor time dilation) occurring, and found its length to be, say, 50 feet, then this length would be the locomotive’s normal length, L₀. And later on, as Scotty and his train rumbled past us through the crossing at the relative speed of 0.866c, we would now observe his locomotive’s length, again, as measured by our rulers, to be contracted, or shortened, to only 25 feet along the direction of its motion, namely, shortened to the length L_C. Reiterating what we had calculated above, then, L_C = 0.5L₀, and particularly, in this case, (25 feet) = 0.5(50 feet). Rumble, young man, rumble...

Figure 2 shows that we would observe Scotty’s locomotive to shorten more and more in the direction of motion, as its speed, relative to us, continuously increased to near that of the speed of light.

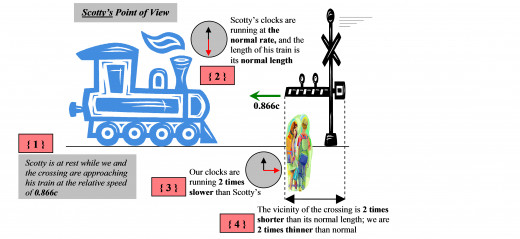
Of course, from Scotty’s point of view, the situation was reversed due to the symmetry of the principle of relativity. To him, the lengths of his train and everything in it, including his two photon clocks, remained at their normal lengths and were NOT contracted whatsoever, while all of his clocks, including again, of course, his two photon clocks, were running at the NORMAL rate of time passage! To Scotty, it was the outside world that was moving at 0.866c instead, and therefore, he observed distances in the outside world to be contracted by the factor 0.5 along the direction of relative motion, and clocks in the outside world to be running 2 times slower than his clocks!

And indeed, just as the astronauts derived the exact same equation as we did for the relativistic time dilation factor, but used their point of view or frame of reference, which was their spaceship, to derive it instead, then so too would Scotty derive the exact same equation as we did for the relativistic distance contraction factor from his point of view or frame of reference, which is his train! For instance, let’s say that we decide to set up the photon Clocks V and H at our train crossing so that Clock V is again in the vertical position, and Clock H is again in the horizontal position (along the direction of the tracks, that is, along the direction of relative motion). Now, from our point of view, we, our two clocks, and the outside world are all at rest with respect to each other. In fact, stating things more briefly, from our point of view standing at the train crossing, the earth itself is at rest. Hence, as observed from our perspective, there can be NO length contraction (NOR time dilation) affecting our two photon clocks. Therefore, from our point of view, Clock V’s photon and Clock H’s photon both travel equal total distances of 2h (where h is, of course, the normal distance between the mirrors), at the always constant speed of light c, to complete their respective ticks.

And as a direct result of this fact, our Clocks V and H must therefore always remain in sync, as observed from our point of view. And why must this be so? This must be so, because if our photon clocks, or, for that matter, if ANY properly working timepieces at rest relative to the earth, were to ever fall out of sync with each other as a result of merely being re-positioned, then we could conclude, without any doubt, that, "Yes, the earth is definitely moving!". And with that conclusion, we would depth charge the principle of relativity and sink it into oblivion yet again!

But what, then, will Scotty predict that he should observe about our photon clocks as his train rumbles through the crossing at the relative speed v? Well, not to beleaguer the point, but from Scotty’s perspective, he and his train are at rest while it is we, our photon clocks, and everything else in the outside world, that is to say, it is the surface of the earth itself that is moving by him and his train at the relative speed v instead. First of all, then, he will observe, just as we had observed about his Clock V, that the photon in our Clock V travels a double diagonal path to complete 1 tick, due to the earth’s relative motion. Secondly, he will also predict that he should observe, just as we had predicted that we should observe about his Clock H, that the photon in our Clock H will travel a forward and backward path to complete 1 tick, again, due to the earth’s relative motion. And, since Scotty will likewise measure the speed of the photons to always equal the constant value c as per the second postulate, then he will therefore ALSO erroneously calculate, just as we had erroneously calculated, that as observed from his point of view, that is, as measured by him using his watches, t_H > t_V ! And hence, his inherently flawed calculation will ALSO lead him to believe that he will observe our Clock H slow down and fall out of sync with our Clock V!

But Scotty knows the principle of relativity all too well by now. And he therefore realizes that if, from our point of view, we were to observe our Clock H to indeed lose sync with our Clock V for no apparent reason, then he knows that we could conclude, without any doubt, that, “Yes, the earth is the one that is truly, absolutely moving!”, thereby chain-sawing the principle of relativity into nice, bite-sized pieces! And so, the lesson to be had in this symmetrical tale of two timepieces is that, contrary to his prediction, Scotty will unavoidably also observe, just as we had observed about his Clock H, that our Clock H is shortened along its length in the horizontal direction by the factor sqrt(1 - v² / c²), so that, as measured from his point of view, t_H = t_V instead! In this manner, our Clocks V and H will be kept in sync, thereby upholding the principle of relativity! And so, Scotty will likewise deduce that

where h_C is the shortened length of our Clock H, as it appears to Scotty, and h is its normal length, as it of course appears to us. And since there is nothing extraordinary about our Clock H, and moreover, since, from Scotty’s point of view, it is the outside world and everything in it that is moving, then not only will Scotty observe our Clock H to be shortened by the factor sqrt(1 - v² / c²) along the direction of relative motion, but in fact, he will observe the outside world itself and everything in it to be shortened by the factor sqrt(1 - v² / c²) along the direction of relative motion! And thus, just as the astronauts demonstrated the symmetry of special relativity’s time dilation phenomenon by deriving exactly the same formula for the time dilation factor as we did, so too has Scotty demonstrated the symmetry of special relativity’s distance contraction phenomenon by deriving exactly the same formula for the distance contraction factor as we did!

Next up in the batting order are those go-get-’em muons that tore through our atmosphere at the alarming relative speed of 0.998c, on their way to colliding with the earth. From the muons’ point of view, it was they who were the ones at rest, while it was the atmosphere and the earth that were hurtling towards them at 0.998c instead. And if we recall, this relative motion resulted in the muons ‘seeing’ – along the direction of motion – a contracted, or shortened travel distance between the earth’s surface and themselves, that was 15.82 times shorter than the normal distance. Here, we stress once more that the meaning of the expression ‘normal distance’ is, in a manner of speaking, “the muons’ travel distance, as measured by observers (such as us), who had been at rest with respect to the earth and the atmosphere in the first place, so that there could be NO length contraction of this distance, as perceived from the observer’s point of view.”

We will now use the same nomenclature for the length contraction formula as before, but we must remember that we are now observing things from the muons’ point of view, such that the atmosphere and the earth were the ones that were moving instead. And so, from the muons’ perspective, if we let L₀ equal the atmosphere’s and earth’s normal, non-contracted travel distance, and L_C equal the contracted travel distance, that is to say, the contracted travel distance that the earth had to traverse in order to slam into the muons, then, the formula must again state that:

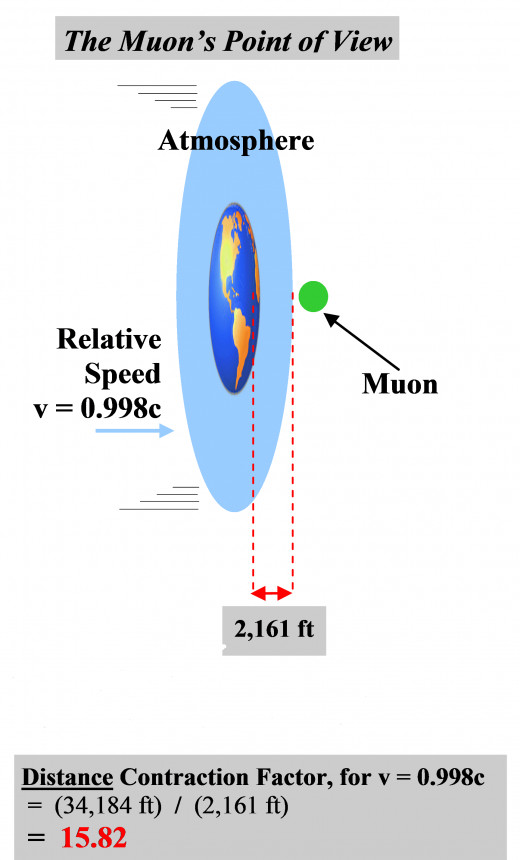
And so, if we now took our gigantic tape measure and measured the distance that the muons had to traverse in order to embed themselves beneath the earth’s crust (which is much easier said than done!), then, as we already know, we would measure this distance to be 34,184 feet. And moreover, since this expanse of atmosphere and earth would (of course) be AT REST relative to us, then this distance of 34,184 feet would therefore be the normal distance, L₀. We know, however, that from the muons’ perspective, the atmosphere and the earth were NOT AT REST relative to them, but were in fact blazing past them at the relative speed of 0.998c! And therefore, the muons would have “observed” the normal distance, that is, the entire 34,184 feet, to be contracted, or compressed to only 2,161 feet along the direction of motion, as measured by the their ‘rulers’ (which, from the muons’ point of view, of course, would be rulers of normal length). Specifically, the normal distance L₀ would have been shortened to the contracted distance L_C. Hence, reiterating what we had calculated above, from the muons’ perspective, L_C = 0.0632L₀, namely, (2,161 feet) = 0.0632(34,184 feet).

Thus, it is also clear from our two examples that as the relative speed increases, so too does the amount of contraction along the direction of motion. Just as with time dilation, however, length contraction becomes perceptible only at speeds that are significant fractions of the speed of light. To appreciate just how negligible these relativistic phenomena are for objects moving at our “everyday” relative speeds, we consider a car being driven at 60 mph relative to the road. At this snail’s pace, the equations of special relativity which we have just derived tell us that we would “observe” a clock inside the car to be ticking at a rate that is 0.0000000000004 % less than the normal rate of time passage, and we would “observe” the length of the car to be contracted to 99.9999999999996 % of its normal length!

[6] We can also visualize the fact that the amount of distance contraction increases as an object’s relative speed becomes greater and greater – specifically, the fact that an object gets shorter and shorter along the direction of its relative motion as its relative speed becomes greater and greater – by investigating the ‘behaviour’ of our three graphs shown below. We imagine that while we are standing at the train crossing, Scotty’s train zooms through it numerous times, each time at a greater, but always constant, relative speed (e.g., the first time through the crossing, his train’s relative speed is 0.1c; the second time through, it is 0.2c; the third time, it is 0.3c, and so on, in gradual increments). And for each time through the crossing, that is to say, for each value of the train’s relative speed, we record the appropriate values, being either calculated or measured from our point of view, onto each of our three graphs. And so…

Our first graph is a plot of the ratio d_H / d_V versus the relative speed v, given that the distance contraction phenomenon DID NOT EXIST AT ALL.

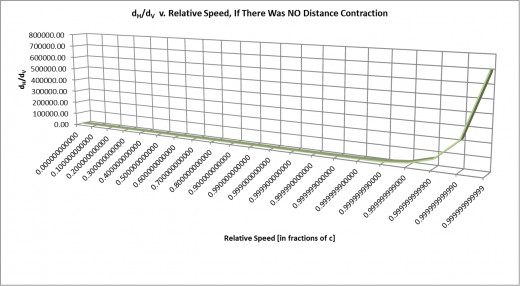
We recall that d_H equals the predicted total forward and backward distance that the photon in Scotty’s Clock H has to travel in order to complete 1 tick, as calculated from our point of view. Correspondingly, d_V equals the actual total double diagonal distance that the photon in Scotty’s Clock V has to travel in order to complete 1 tick, as observed from our point of view. And v is, of course, the speed of Scotty’s train relative to us. Hence, our first graph is ‘saying’, in essence, that: If the relativistic distance contraction phenomenon did not exist, then as observed from our point of view, as the relative speed v becomes greater and greater, the ratio between these two distances, specifically, d_H / d_V, would increase at a faster and faster rate, as shown by the latter portion of our first graph (we must note, at this point, that this “faster and faster rate” is present throughout our entire graph as the relative speed increases, but becomes perceivable only in the latter portion, as the relative speeds approach the speed of light). Hence, we would predict, exactly as we did earlier in our discussion, that as the relative speed v becomes greater and greater, then the photon travel distance d_H itself would become disproportionately greater and greater than the photon travel distance d_V itself, as observed from our point of view, if relativistic distance contraction did not exist. And since Clock H’s and Clock V’s photons must both always travel at the universally constant speed of light c, then our prediction that d_H > d_V would lead us to also predict that we would observe Clock H fall further and further out of synchronization with Clock V as the relative speed of Scotty’s train becomes greater and greater with each pass through the crossing!

We know, however, that this loss of synchronization cannot happen, because of the fact that Scotty is, by the principle of relativity (i.e., the first postulate), completely justified in declaring that he and his train are at rest. Therefore, from Scotty’s point of view, there can be NO distance contraction (nor time dilation) at work within the confines of his train! And therefore, Scotty must and will observe his Clock H and his Clock V maintain their synchronization. Thus, we must and will also observe his Clock H and his Clock V maintain their synchronization (although we will, additionally, observe both of his clocks ticking more and more slowly than our clocks as his train’s relative speed increases, because of time dilation).

But now, how can Mother Nature ‘remedy’ our first graph so that it shows that d_H = d_V and NOT d_H > d_V, for any and all values of the relative speed v, so that both photons travel equal distances in order to complete their respective ticks, thereby keeping Clock H and Clock V in sync from our point of view also, as they must be? Well, we already know that the remedy is the relativistic distance contraction phenomenon, whose distance contraction factor, which we’ll abbreviate as “DCF”, equals

Thus, we have our second graph, which is a plot of the DCF versus the relative speed v.

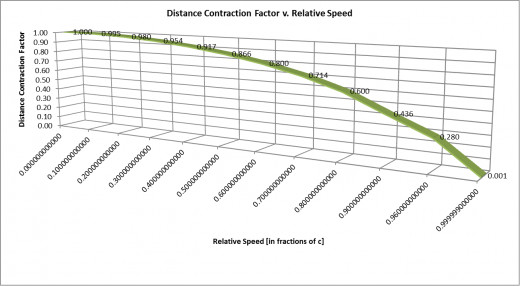
Let us take note of this graph’s important properties. First of all, when the relative speed of Scotty’s train equals 0, then the DCF has a value of 1. Surely, this must be the case, because it means that his train is at rest relative to us (and vice versa), and hence there can be no distance contraction (nor time dilation) at work from our (or from Scotty’s) point of view. Stating this mathematically,

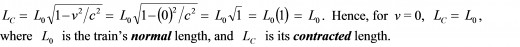
Secondly, as the relative speed of his train increases with each pass through the crossing, the value of the DCF decreases at a faster and faster rate. But why does the DCF continue to decrease disproportionately as the relative speed of Scotty’s train becomes greater and greater? It does so in order to COUNTERACT the disproportionately INCREASING value of the ratio d_H / d_V. Furthermore, it turns out that this lopsided ratio between d_H and d_V, which is plotted as a function of v in our first graph, is given by the equation

But, as we have discussed to great lengths by now, reality itself demands that Scotty’s Clock H and Clock V remain in sync. And therefore, the equation

must be incorrect, because we already know that as observed from our point of view, the photon travel distance d_H must CONTRACT, or SHORTEN in length so that it equals d_V, in order for Clock H to remain in sync with Clock V. Hence, this requirement that d_H = d_V immediately tells us that the correct equation for the ratio must simply be:

So, how does Mommy Natural get to this latter equation? Enter the relativistic Distance Contraction Factor, or DCF, as we have called it, whose expression we know to be equal to sqrt(1 - v² / c²). Now, let’s SHORTEN the distance d_H in our incorrect equation by multiplying both sides of this equation by the DCF:

Hence, as observed from our point of view, if Clock H itself contracts, or shortens (along the direction of the train’s relative motion) by a factor equal to the DCF, then Clock H’s photon travel distance d_H will also shorten by this same factor, such that it always equals the photon travel distance d_V for any and all relative speeds, thereby keeping Clock H in sync with Clock V, as they must be. This result is clearly revealed by our third graph.

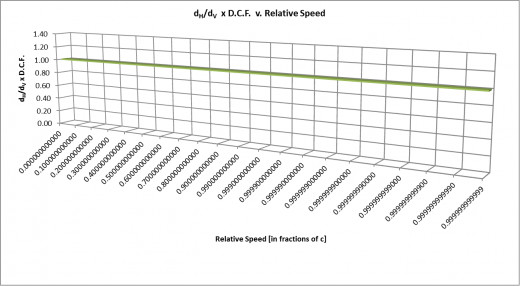
In a manner of speaking, then: GRAPH 3 = GRAPH 1 x GRAPH 2, for any and all relative speeds.