Want To Ace GRE Math? Make Abstract Problems Easier to Understand with This Technique

Here’s the double-whammy of GRE math problems! I explained in a previous hub that number property problems are a favorite of test writers because by their very nature they involve abstract thinking. Pile this abstract thinking on top of the unfamiliar logic demanded by the Quantitative Comparison format, and some of these problems definitely qualify for the designation “brain teaser.” But I’ve got good news once again! And once again, it stems from the strategy I’ve been touting: applying actual numbers. Actual numbers allow you to think about number properties more concretely. Applying actual numbers to the QC format, as we’ve seen, gives you a straightforward method for solving QC problems.

So let’s put the strategy to work on a couple QC number-property problems, and see what kind of benefit it provides.

Remainders fall under the category of number properties because they are related to divisibility, which is related to factors and multiples. As it relates to math, “remainder” is a term that you may not have used since middle school. If you divide 21 by 5 on a calculator, you get 4.2, no remainder shows up. But the GRE requires you to shake the rust off this ancient concept and instead say, “Five divides evenly into 20 four times, and this leaves a remainder of 1,” or provide the answer “4 r. 1.” (Don’t start getting nervous …. Remember that the number of math concepts with which you need to become reacquainted is relatively small.)

If you’re comfortable working this problem abstractly, it undoubtedly is faster than applying actual numbers. Briefly, since 10 is a multiple of 5, adding it to n has no impact on the remainder. So the quantities will always be equal, and you’ll select (C) for your answer. But if these last couple sentences make no sense to you; or if you vaguely recognize these concepts but know that they are stored in the deep, nearly inaccessible recesses of your mind; then apply actual numbers! Although you may use more time than your fellow test-takers who approach this problem abstractly, you still get it right!

Here’s how: Just as I did with the problems I introduced in the last hub, I’ll start by picking any value for n that complies with the rules. This means that n must be positive and it must be an integer (whole number). I could simply use n = 1, but starting with a number smaller than 5 can get confusing. So instead, let’s start with n = 12:

Quantity A: 12 ÷ 5 = 2, remainder 2
Quantity B: 22 ÷ 5 = 4, remainder 2

(Unless you have a third- or fourth-grader, it’s been a while! Let me spell it out: When I divide 12 by 5, I get 2 because 2 x 5 = 10, and 10 is the multiple of 5 that is as close as I can get to 12 without going over. Since 2 x 5 = 10, I have 2 “leftover” units. The leftovers are the remainder.)

With n = 12, each quantity has a remainder of 2, so they are equal. Right away I can cross off answer choices (A) and (B).

Now the question is whether I can get the relationship to change. Let’s try an n that’s different from 22. How about 149? It’s got 3 digits, and it’s odd.

Quantity A = 149 ÷ 5 = 29 remainder 4
Quantity B = 159 ÷ 5 = 31 remainder 4

The remainders are still equal. Let me try one other thing. How about a prime number? Let’s go with 43.

Quantity A = 43 ÷ 5 = 8 remainder 3
Quantity B = 53 ÷ 5 = 10 remainder 3

By now, most test takers would either see the pattern or decide that it’s worth the risk of going no further and selecting answer choice (C).

Here is one more. This one employs the concept of prime factors. Prime factors are numbers that have exactly two factors: themselves and 1. Examples include 2, 3, 5, 7, 11, 13, 17 and 19. (Shall I assure you one more time? There really aren’t very many math concepts with which you need to get reacquainted! And when you’ve finished working through the two problems in this hub, you’ll have tackled two of them!)

Abstract thinkers: Since 9 and 8 each introduce exactly one additional prime factor, you may be thinking that the answer should be (C). However, since the quantities specify the number of different prime factors, you’ll need to consider the impact of an n that already includes 2 or 3 as a prime factor. So even for someone pretty handy with math, it’s a good idea to apply actual numbers just to check your thinking.

I start by picking a value for n, as usual. And once again with this problem, since I’m factoring the numbers I’d rather start with something bigger than my usual choice of n = 1 or 2. So let’s try n = 10.

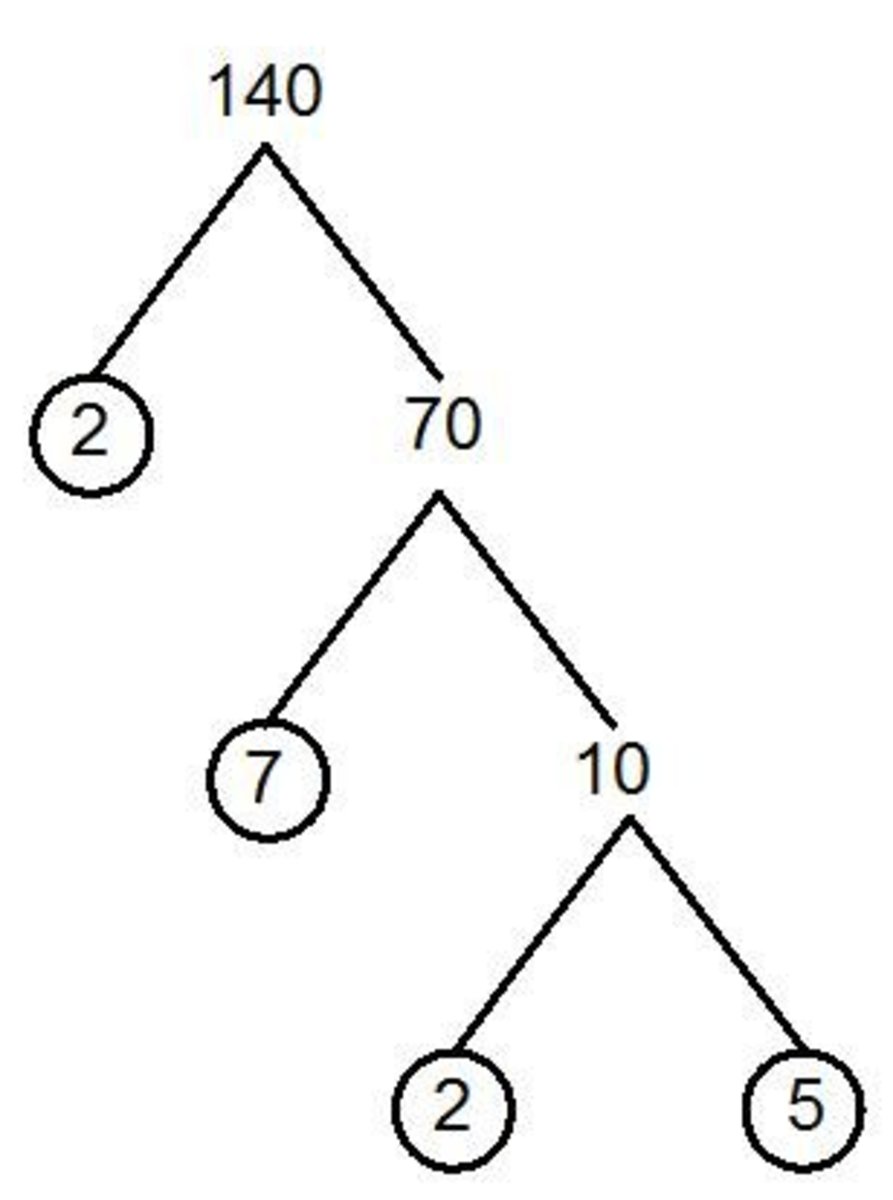
Quantity A: The prime factors of 90 are 2 x 3 x 3 x 5; so the number of different prime factors is 3
Quantity B: The prime factors of 80 are 2 x 2 x 2 x 2 x 5; so the number of different prime factors is 2

QA > QB, so cross off answer choices (B) and (C).

Can I get the relationship to change? Let me pick an n that is different from 10. Let’s try an odd number, like 11.

Quantity A: The prime factors of 99 are 3 x 3 x 11; so the number of different prime factors is 2
Quantity B: The prime factors of 88 are 2 x 2 x 2 x 11; so the number of different prime factors is 2

The quantities are equal, so the relationship changed. My answer is (D).

In case you’re wondering how I came up with the values of n that I used, for the most part, I picked them because I felt like it. Some of my students have thought that there are some hidden criteria for selecting values. Nope. Pick what you like. The only caveats are (1) be sure that the values comply with the problem’s rules, and (2) try values from the different categories (e.g. 0 or 1, negatives, proper fractions).

Give it a try! And let me know how you make out. All the best in your test preparations!