Want To Ace GRE Math? Use This Technique on Quantitative Comparison Problems

When I introduced the GRE Quantitative Comparison (QC) format and presented a step-by-step strategy for solving these problems, I finished by pointing out that the QC format lends itself to the technique of applying actual numbers. In my series of hubs on applying actual numbers to regular multiple-choice problems, I highlighted the fact that this technique reduces many algebra problems to basic arithmetic. The same is true when I apply actual numbers to QC problems. I hope you recognize this as very good news for math-phobic test takers. If math variables make your palms sweat, then you can move away from them in many (if not most) GRE math problems.

For multiple-choice and QC problems alike, the first step of applying actual numbers is to pick numbers that comply with the problems “rules.” The rules in the question may be:

• given equations or inequalities (e.g. j – k = 3);
• number properties (e.g. “the even integer x”); or
• diagrams or wording that limit valid values (e.g. “radius” can only be a positive number, and “the number of people remaining in the room” can only be a positive whole number).

Once I’ve selected values, I apply them to the quantities and determine their relationship with this first set of numbers. I can immediately cross off two answer choices in QC problems – the two that don’t correspond to the relationship I just found between the two quantities.

Now my procedure with QC diverges from the procedures I used with regular multiple-choice problems. My goal is to try to get the relationship between the two quantities to change. So I’m going to try numbers that are distinctly different from my first set of numbers. As long as these values follow the rules, I might try:

• even numbers if my previous numbers were odd
• negative numbers
• fractions between 0 and 1 (i.e. “proper fractions”)
• numbers near or far away from the boundaries created by inequalities (e.g. if x < 1, I might choose 0.99999 or -100)
• because of their special properties, 0 and 1

One of three things will cause me to select my final answer:

1. As soon as the relationship between Quantity A and Quantity B is different from the relationship I found with the first set of numbers, I choose answer choice (D).
2. I may recognize a math concept that ensures the relationship will not change (e.g. I may realize that Quantity A is always positive and Quantity B is always negative).
3. I may have tried several values representing types listed above, and the relationship still has not changed.

In the case of #2 or #3, I will select the answer choice – (A), (B) or (C) – that corresponds to the relationship between the quantities.

Let’s put this approach to work!

Notice in this problem that the values of x and y can be anything – whole numbers, fractions, negatives, zero, etc. – as long as x is greater than y. (By the way, one of the silliest yet easiest mistakes to make on a GRE problem is misread an inequality. If you pick values such that x is less than y, this might lead you to a wrong answer choice.) Any set of numbers will do for the first round, so I’ll keep it simple: x = 2 and y = 1. Then

Quantity A = |2 + 1| = 3
Quantity B = |2 – 1| = 1

Since QA > QB, I will eliminate answer choices (B) and (C). Now I’ll see if I can get the relationship to change: Since 0 is in play, I’m betting that its special properties may cause the relationship to change. So I’ll leave x at 2 and change y to 0. Then

Quantity A = |2 + 0| = 2
Quantity B = |2 – 0| = 2

They are equal … so I’m done! The answer is (D).

Let’s do one more here, and I’ll cover QC problems involving number properties in my last hub on this topic.

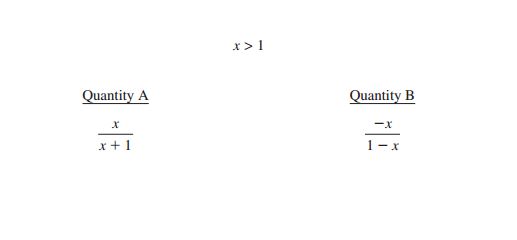
For this problem, I can pick any value for x as long as it’s greater than 1. So again, I’ll start simple, with x = 2. Then

(Did you know that the GRE makes a simple calculator available to you during the test? If negatives are not your strong suit, you can check your work with the calculator.)

With QA < QB, I’ll cross off answer choices (A) and (C). To try to change the relationship, I’d like to try any of the special values that are allowed by the rule; but x > 1 means that proper fractions, 0, and negatives are not allowed. I’d like to keep the math simple; since I have x + 1 as a denominator, I’m going to use x = 9 (so I end up with a denominator of 10):

It is still the case that QA < QB. I’ll try getting really close to the boundary next, with x = 1.1:

This move not only fails to change the relationship, it also makes the difference between the two values even greater.

So I haven’t changed the relationship yet. Am I ready to select answer choice (B)? Let me suggest two scenarios:

Some of you, when you see the actual numbers in the fractions, may recognize that Quantity A’s numerator will always be larger than the denominator, which means that this quantity will always be less than 1. On the other hand, Quantity B’s numerator is always larger than the denominator, which means it will always be greater than 1. So you will confidently be able to say that QA will always be less than QB (or, as answer choice (B) puts it, QB > QA), so you’ll select (B).

Others of you may not have the insight I just described. In this case, you’ve tried all of the available categories. To be certain, you might want to try a very large value, like x = 1,000:

With the relationship still not changing after four very different values for x, at this point you will select (B) – perhaps with less confidence than your fellow test-takers, but correctly nonetheless!

At this point some of my students express a concern about how many sets of numbers they should pick before deciding that the relationship is not going to change. In my experience, three or four sets has always been sufficient.