What is Pythagorean Theorem – A Recap of the Immutable Pythagorean Equation
![By Galilea at de.wikipedia [GFDL (http://www.gnu.org/copyleft/fdl.html) or CC-BY-SA-3.0 (www.creativecommons.org/licenses/by-sa/3.0/)], from Wikimedia Commons By Galilea at de.wikipedia [GFDL (http://www.gnu.org/copyleft/fdl.html) or CC-BY-SA-3.0 (www.creativecommons.org/licenses/by-sa/3.0/)], from Wikimedia Commons](https://usercontent2.hubstatic.com/4686901.jpg)
A brief history of the Pythagorean Theorem
Over 2,000 years ago, a Greek mathematician and philosopher named Pythagoras (569-500 B.C.E.) who spent most of his time contemplating about mathematics, astronomy and music came up with an uncomplicated mathematical equation which became an established geometric proof that provides a mathematical reasoning which substantiates for the fundamental truth about how shapes and figures fit together. The theorem which was named after Pythagoras was one of the earliest mathematical concept ever known to ancient civilization, and since then, the Pythagorean Theorem endured throughout history as the most important mathematical expression ever conceived in all of elementary mathematics due to its significance and usefulness in modern mathematical applications relevant in the field of engineering, architecture, the construction industry and science.
The theory helped influence the progression and advancement of modern mathematics. Even Albert Einstein used Pythagoras' Theorem as the foundation for his metric equations of Special Relativity. The ancient Egyptians were also known to have a practical understanding of the theory long before Pythagoras' discovery, as could be proven by the ancient Egyptian's knowledge of selecting the right triangle as their main geometrical idea in the construction and building of their triangular pyramids.
![Atamari [CC-BY-SA-3.0 (www.creativecommons.org/licenses/by-sa/3.0)], via Wikimedia Commons Atamari [CC-BY-SA-3.0 (www.creativecommons.org/licenses/by-sa/3.0)], via Wikimedia Commons](https://usercontent1.hubstatic.com/4686914_f520.jpg)
Pythagoras and the Pythagoreans
Pythagoras devoted much of his mathematical studies with the brotherhood of Pythagoreans, a cult-like group he formed dedicated to the purpose of achieving mystical and spiritual knowledge and understanding of numbers, from which they religiously believed that numbers supremely rules the universe, and which they worshiped with symbols, rituals and prayers. Delighted with the astounding discovery of the theorem, Pythagoras celebrated the achievement by sacrificing 100 oxen to credit for his success with the famous theory. However, it is not historically verifiable to prove that Pythagoras is actually the sole author of the famous theorem since many of the group's mathematical theories were believed to be contributed by students from within the brotherhood who pledged to a vow of utmost secrecy never to divulge many of their geometric proofs and mathematical hypothesis to the public.
Useful Reading Resources
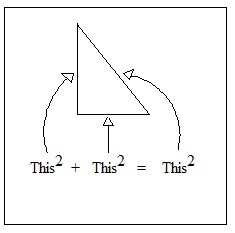
The Pythagorean Equation
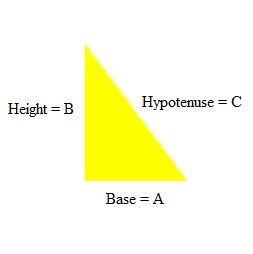
The equation of the Pythagorean Theorem is simply expressed as a2 + b2 = c2, which means that the sum of the squares of the two sides of a given right triangle is equivalent to the square of the longest side of the triangle known as the hypotenuse. To better understand what this means, refer to the diagram on the right, the equation shown on the drawing illustrates that the sum of the squares of the two sides that makes up the L-shape part of the triangle is equivalent to the square of the inclined side of the triangle or the slanting line leaning on the L-shape side of the triangle.
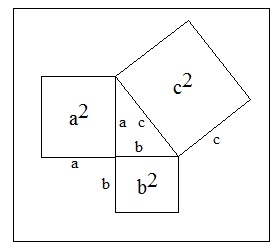
In mathematical expression, the
Pythagorean theorem or Pythagoras' theorem is Geometrically related
to the three sides of a right triangle, where c represents the
area of the square whose side is the hypotenuse (the side opposite
the right angle which is the longest side of the right triangle)
which is equally the sum of the areas of the squares whose sides are
the other two legs a and b (the two sides that meet at
a right angle and intersects with the hypotenuse).
This can be summarized further as: The square on the hypotenuse is equal to the sum of the squares on the other two sides. If we let c be the length of the hypotenuse and a and b be the lengths of the other two sides, the theorem can be expressed as the equation: a2 + b2 = c2. This simple equation establishes a basic relation among the three sides of a right triangle that provides an easy computation for the length of any side with unknown value which can be derived from the known values of the lengths of the other two sides.
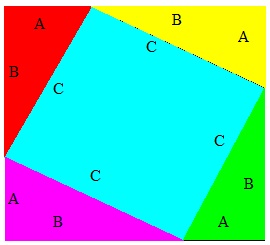
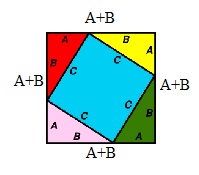
Generalization and Derivation of Pythagorean Proofs by Algebraic Proof
An algebraic variant of this proof is
provided by the following reasoning. Looking at the illustration on
the right side of this page which shows a large square with identical
right triangles on each corners (red, yellow, green and violet), the
area of each of these four triangles is given by an angle
corresponding with the side of length C, which is occupied by the center blue square as shown on the figure.
The area of the yellow triangle shown on the right is computed as:
½ AB = area of a right triangle which
is ½ base x height.
The A-side angle and B-side angle of
each of the colored triangles (red, yellow, green and violet) are complementary angles, so each of the
angles of the blue area in the middle is a right angle, making this
area a square with side length C. The area of this square is C2, which was derived by the following equation:
Area of the blue square shown on the right = Height x Width = C x
C = C2
Thus, the area of everything together
is given by:
4 small colored triangles (red, yellow, green and violet) + one blue square = 4(½
AB) + C2 --> equation 1
However, as the large outer side square has sides of length A + B, we can also calculate its area as (A + B)2, which expands to A2 + 2AB + B2 –> equation 2, Derived from the following equation
Area of outer side of the square:
(A+B) x (A+B) = (A+B)2
Algebraically:
(A+B)(A+B)
=A2+AB+AB+B2
= A2+2AB+ B2 –> equation 2
But equation 2 = equation 1, so….
A2 + 2AB + B2 =
4(½ AB) + C2
(Distribution of the 4)….. A2 + 2AB + B2 = (4/2 AB) + C2
A2 + 2AB + B2 = 2AB + C2
(Transposing of 2AB)…. A2 + (2AB - 2AB) + B2 = C2
Since 2AB – 2AB = 0 therefore,
A2 + 0 + B2 = C2
A2 + B2 = C2 -->
Pythagorean Theorem
Useful Reading Resources
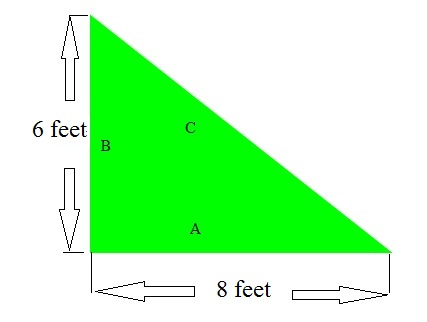
Exercise 1
Solve for the hypotenuse C of the right triangle shown on the right by using the Pythagorean Theorem…
Solution by Pythagorean Theorem:
A2 + B2 = C2
C2 = A2 + B2
C2 = (8)2 + (6)2
C2 = 64 + 36
C2 = 64 + 36
C = √100
C = 10 ft
Exercise 2
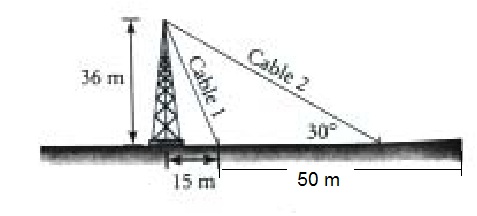
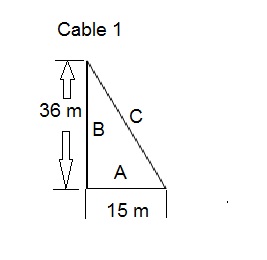
Find the length of each cable in the figure shown on the right.
Cable 1:
A2 + B2 = C2
C2 = A2 + B2
C2 = (15)2 + (36)2
C2 =225 + 1296
C2 = 225 + 1296
C = √1521
C = 39 m
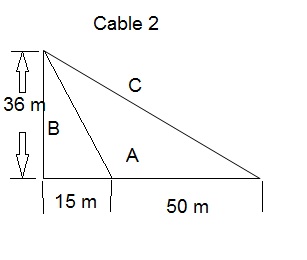
Cable 2:
A = 15m + 50m = 65m
A2 + B2 = C2
C2 = A2 + B2
C2 = (65)2 + (36)2
C2 =4225 + 1296
C2 = 4225 + 1296
C = √5521
C = 74.30 m
Exercise 3
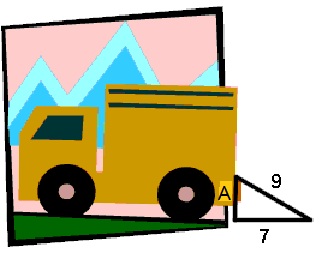
A ramp was constructed to load a truck. If the ramp is 9 feet long and the horizontal distance from the bottom of the ramp to the truck is 7 feet, what is the vertical height of the ramp?
Since the ramp is described as having horizontal and vertical measurements, a right angle is implied. Solve using the Pythagorean Theorem…
Solution:
C2 = A2 + B2
92 = A2 + 72
81 = A2 + 49
81- 49 = A2
√32 = A
5.66 = A
The height of the ramp is 5.7 feet. The ramp will allow packages to be loaded into an area of the truck that is too high to be reached from the ground.
Exercise 4
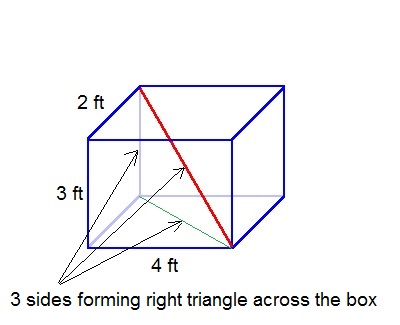
A 3D problem:
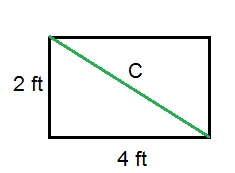
We have a wooden box that measures 4 ft. by 3 ft. by 2 ft.: Figure out: What is the longest straight pole, like the red one, that you can have inside the box?
Equation 1:
First solve for C on the bottom of the box:
C2 = A2 + B2
C2 = (4)2 + (2)2
C2 = 16 + 4
C2 = 20
C = √20
C = 4.47 ft
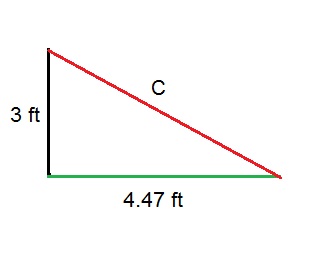
Equation 2:
Next solve for C of the right triangle across the box:
C2 = A2 + B2
C2 = (4.47)2 + (3)2
C2 = 19.98 + 9
C2 = 28.98
C = √28.98
C = 5.38 ft
The longest straight pole that can be placed inside the box is 5.38 feet.

Exercise 5
You're locked out of your house and the only open window is on the second floor, 25 feet above the ground. You need to borrow a ladder from one of your neighbors. There's a bush along the edge of the house, so you'll have to place the ladder 10 feet from the house. What length of ladder do you need to reach the window?
Solution:
Think of the ladder as the hypotenuse of a right triangle. Since you know the length of the other two sides of the triangle, use the Pythagorean theorem to find the length of the hypotenuse…
By Pythagorean Theorem:
C2 = A2 + B2
C2 = (10)2 + (25)2
C2 = 100 + 625
C2 = 725
C = √725
C = 26.92 feet – the length of the ladder needed to reach the window…
Useful Reading Resources
I, the copyright holder of this work, hereby publish it under the following license:
What is Pythagorean Theorem – A Recap of the Immutable Pythagorean Equation by ianjonas is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License.