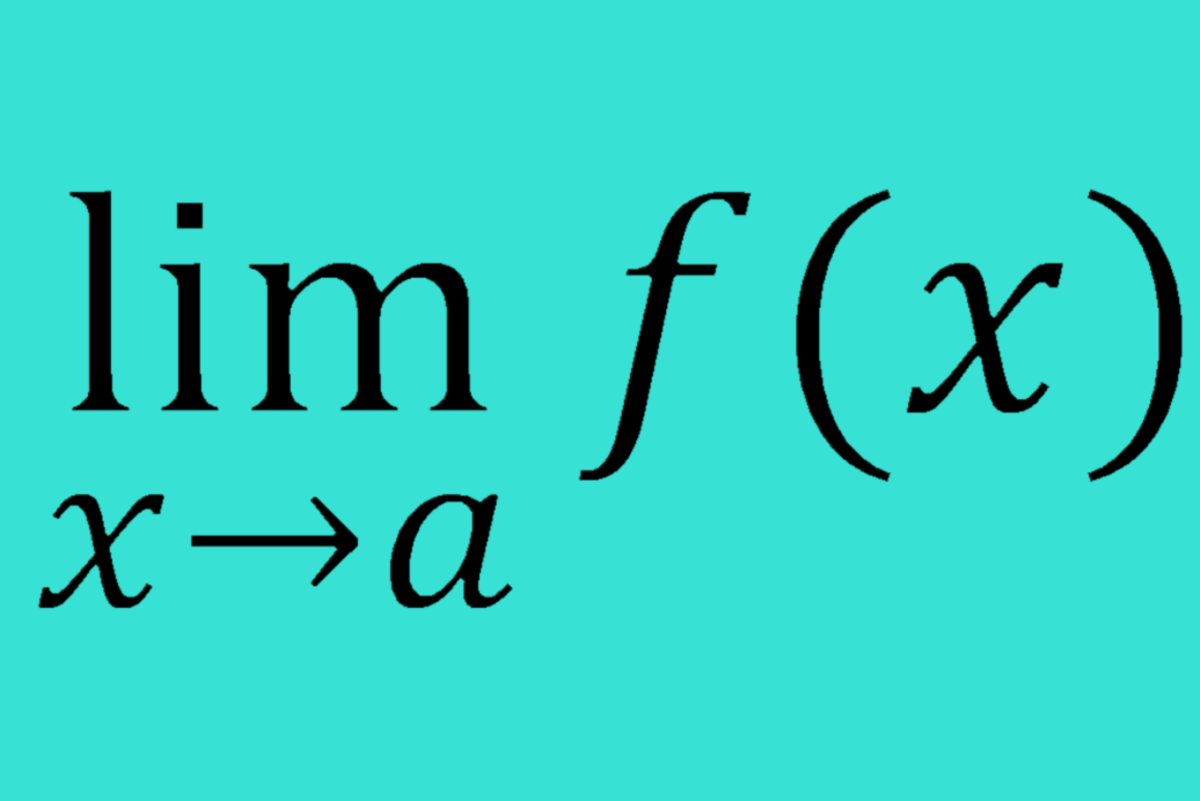e, The Base of the Natural Logarithms--limit defined:

1. Paragraphs 8, 9 and 10 address tornadoes, planes and God.

AN AMAZING CONSTANT OF MATHEMATICS:

2. The constant, e, is fascinating! In mathematics it is ubiquitous being associated in the following distributions: gamma, beta; discrete and continuous uniform; Bernoulli, binomial, geometric, hypergeometric, Poisson, exponential, normal( a biggie in statistics), chi square, student's T( next to normal for biggieness), multivariate normal, bivariate, lognormal, the F distribution, and many more. You will see it in Laplace transforms, and Fourier transforms and analysis. As you saw at hub#12.12( Complex logs) it can transform functions and numbers into the complex plane to solve "impossible" problems. It is used in De Moivre's theorem to find 6 roots of a --1, or roots and various powers of complex numbers. It is, in my opinion, indispensable in analysis, and solving differential equations. The list is nearly endless.

AN AMAZING CONSTANT IN SCIENCE, AND MORE:

3. In science it is associated with entropy, biological systems, theoretical physics, cosmology, thermodynamics, physical chemistry, and the natural decay of just about everything. In economics it is used to find the interest rate when compounded continuously. Concerning the Bible, one site( link to it) had this to say: "A numerical analysis shows that these Biblical patriarch's longevity follows a base e exponential decay with tight standard deviation where e is the natural constant, e = 2.718 . . . ". Or in other words from Adam to Moses the decline in the patriarch's lifespan followed the base e exponential decay. I personally believe God built this constant into the structure of space itself, and if we begin to figure out how then we will get insight into the macro structure of space. I believe the micro structure has to do with the storage of information that the electromagnetic force requires to build complex organic molecules and systems.

WORK FROM L1 THROUGH L4 EXPLAINED:

4. John Napier used e "in the table of an appendix of a work on logarithms"( Wikipedia), but "the discovery of the constant itself is credited to Jacob Bernoulli" when he wanted to determine the value of L3 below. L3 is very similar to the formula for the amount of money earned, A, with P invested after t years invested at r interest rate compounded with n periods. That formula is A = P( 1 + (r / n))^nt. The limit at L3 takes n, the number of periods, and makes it approach infinity; thereby, making the time duration of the period to approach zero. This is continuous compounding. Both L1 and L3 are used in textbooks to define e. L2 is just showing how we can get from L1 to L3. L4 is the first step in solving a problem; it says "find". Yap, that's the only way to arrive at any destination--must take the first step.

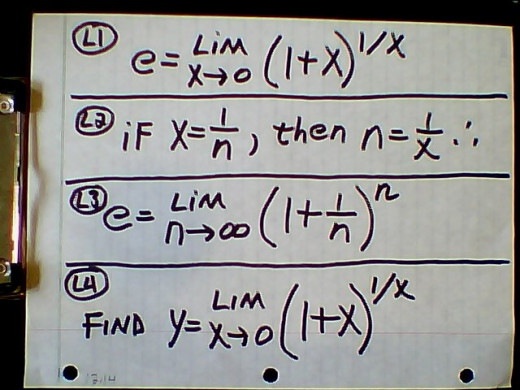
L5 THROUGH L8 EXPLAINED:

5. Take a look at L4. If X approaches zero then that limit is apparently saying, "What is one raised to the infinite power?" Well, it is 1, right? After all 1 times 1 times 1 times 1 times . . . is always one. We can do this forever, and it will still be one. We expect the answer to be 1. The amazing aspect of mathematical limits is the answer is very often nothing what you would expect. This is what L9 points out. Technically, it is not 1^∞, which is 1 raised to infinity. X is approaching zero, it never reaches zero. So it is never exactly 1 in the parentheses, and the exponent is never infinity. At L5 we take the natural logarithm on both sides of the equation, and here at L5 the limit is part of the argument of the log function. The laws of limits allow us to put it( the limit operator) on the outside of the log function. L6 and L7 shows an intuitive reason why this is allowed. The limit function operates on X. What does it matter if it tells X to approach 7 on the inside of the square function or the outside of it? I know that is not a rigorous treatment of the concept but it makes sense to me. So we put the limit operator on the outside at L8.

L10 THROUGH L14 EXPLAINED:

6. The limit at L4 just gives us 1 raised to infinity, which is 1^∞, but if we want to use L'Hopital we must get the limit function into the form, 0 / 0. At L10 the laws of logs tells us we can put the exponent, 1 / X, in front of the log function, and L11 uses basic arithmetic to put the X in the denominator. If we take the limit of X approaches zero at L11 that fraction goes to 0 divided by 0. As explained at hub#12.3( Limits) if the limit has the form 0 / 0 then we can use L'Hopital's rule to solve it; therefore, we take the derivative of both the numerator and denominator separately at L12, which gives the result at L13. Now we can take the limit of X approaches zero and it gives 1 divided by 1, which is 1 at L14. Also at L14 we convert the log equation, In(Y) = 1, to its exponential form( some authors use the verb exponentiate). We finally arrive at the answer of Y = e at L14. So the limit of L1 does indeed equal the base of the natural logarithms, which is about 2.71828.

L15 THROUGH L21 EXPLAINED:

7. These steps do the same thing with L3 as what was done with L1, but what is significantly different is L17. It is in the form of ∞^0( infinity raised to the zero power). This is not the form we want if we want to use L'Hopital; however, we can convert it to the 0 / 0 form at L18. We simply put it in the denominator as 1 / n. This is so simple, and yet so clever. This complex fraction can easily be put back into the form of L16 by multiplying the complex fraction by 1 using n / n; therefore, L16 and L18 are the exact same equation but in different forms. The form of L18 gives us 0 / 0 so we can use L'Hopital again. It is a little more complicated because we had to use the chain rule in the numerator at L20, but that enabled us to cancel out the -1 / n^2 term leaving us L21. Taking the limit at L21 and exponentiating gives us the same answer as L14 gave.

TORNADOES, NUTS, BOLTS, WIRE AND EVOLUTION:

8. Whenever a debate ensues between a creationist and evolutionist, one argument that usually is brought to the forefront by the Christian is the tornado analogy: What are the chances of a tornado going through an aircraft junkyard and leaving behind an assembled Boeing 747 in good working order? It is a very good argument that I have used countless times myself. It is impossible! Evolutionists will argue that given enough time it could happen. No, it will never happen. The reason is entropy, which is, for our purposes here, the tendency of all things to go from order to disorder. Time is the enemy of order, assembly, building and construction; by no stretch of the imagination is it an ally to beneficial structures designed for a purpose. Let us say you grab some nuts and bolts, wire and instruments, and start tossing them all in the air. I'll allow you to have a large box so when everything falls, it will be in the box so you can immediately toss is back into the sky. If by some minor miracle a bolt gets slightly screwed into a nut, the correct nut, then that minor construction will be destroyed by continued tossing. The probability of destruction is much higher than that of construction. All favorable constructions will be destroyed as time marches on. This is why the argument by evolutionists claiming that favorable constructions will occur over eons of time is simpleminded, nonsensical and ineffectual. The more time you have, the less the chances of favorable constructions building upon more suitable constructions into systems that can work together. The same argument applies to the wire and instruments. It would be a major miracle, not a minor one, for the right size wire to solder itself to the correct location on the correct instrument( a fuel or altitude gauge, for example). Then as you are tossing the parts in the air, what are the chances of the other end of the wire soldering itself onto the proper location while the first construction stays intact?

GOD IS THE CREATOR THROUGH JESUS CHRIST---NO EXCUSES ALLOWED!

9. Romans 1:20 states we are all without excuse because creation itself testifies that God is the Creator, and it essentially says this is a no-brainer. We do not need the Bible to know that God exists and is the Creator. An atheist can choose to ignore the evidence, and come up with fatuous and ridiculous conjectures on how creation came about, but that is a foolish choice with miserable and lamentable consequences attached to it, which will last for eternity.

10. If you are called( Matthew 22:14), and drawn( John 6:44) then you have a decision to make. Begin to study the Bible, and be prepared for attacks of lies and sophistry to lead you away from the true path to salvation. A good example of the sophistry I'm referring to is pointed out by North Wind in Bible quotations . . . . She gives about four good examples, but my favorite is the last one quoting John 3:16. Nearly everyone has heard that verse quoted, and many of those people blithely hop around thinking goodie I'm saved, and yet they are totally oblivious to the conditions attached to that verse,and those conditions North Wind points out.