What does E = mc^2 mean?

Einstein's Famous Equation
E = mc2 has been called the world's most famous equation. We dare say it's the world's only famous equation, as you don't hear the average Joe or Kitty going on about, say, Schrödinger's or Nernst's equation down at the coffee shop. We also dare say there's many people who can quote Einstein's equation but don't quite know what it really means.
What does it really mean?
E = mc^2 explained
Here's the good news: although many things in physics are indeed complicated, the concepts needed to understand E = mc2 are not. No other equation so simple has had such a profound effect on society, both good and bad. We dare say understanding E = mc2 is mostly a question of having it explained clearly.
Below, we take on Einstein's famous equation. Or rather, we take it apart. Three parts, to be specific: the E, the m, and the c. As our mechanic might say, we'll disassemble E=mc2, clean and oil the pieces, and put everything back together. Then we'll hand you a bill for $1500. (Ha! We kid the greasy bastards down at the dealership.)
However, before we start getting our hands dirty, let's first sum up the big picture.

The Big Picture
Here's the big picture: E=mc2 states that mass and energy are interchangeable. You can even say mass and energy are the same thing. Two sides of the same coin. Tomato, tomahto. A rose by a different name.
Furthermore, not only does the equation tell you mass and energy are interchangeable, it tells you how much energy you can convert a given amount of mass into. In words: the amount of energy (E) you get is the amount of mass (m) times the square of the speed of light (c). To make the numbers work out, you have to use a particular set of units - energy in joules, mass in grams, and speed in meters per second - but that's not important to understand the big picture. What you should note for now is that the speed of light - whether you measure it in meters per second, miles per hour, or furlongs per fortnight - is a huge number. And the speed of light squared is even huger. This has important consequences, as we shall see later.
To explain E=mc2 in more detail, we need to take some time to explain energy, mass, and the speed of light. Mass and the speed of light are pretty straightforward, but energy - the way physics defines it - takes a little effort to explain. So we will save energy for last. In fact, let's work backwards through E=mc2, starting with c, the speed of light.

The Speed of Light (c)
The speed of light is, well, the speed of light. Lots of experiments over the years have confirmed that light propagates with a large but finite velocity. Turn on a light here and folks over there will only see it after the light has traveled to them.
How fast? A handy ballpark figure is 186,000 miles per second. In metric, that's about 300,000 kilometers per second.
These numbers are so big it's hard to get a feel for what they mean. So let's think about a source of light that is very far away. The sun, for example, is about 90 million miles away. Going by car, and never stopping for gas, it would take about a million years to get there. Or, consider something faster: the maximum speed of the space shuttle is about 24,000 mph (or was, before NASA pulled the plug). Flying at that speed, it would take about half a year to get to the sun (the longest shuttle mission ever -- STS 80 -- only lasted 17 days).
In contrast, it takes light only about 8 minutes to get from the sun to earth. If the sun blinked off, or changed color, or grew fur, or just up and exploded, we would have 8 minutes of glorious ignorance before we found out.
The point is that c is a very big number. We may have mentioned this once or twice already.

Mass (m)
Mass is easy: it is the amount of "stuff" you have. You might think that mass is what you measure when you weigh something. You should now imagine your high-school chemistry teacher glowering at you for saying such a thing. Weight and mass are related but not identical. Weight is the gravitational force exerted on a mass. Put a bowling ball on a scale on Earth and you will get a different number than if you put the same bowling ball on the same scale on the moon. But the mass of the bowling ball is the same in both cases.

Energy (E)
The definition of energy is a little long-winded because energy in physics is an umbrella concept used to turn vague everyday experience into something precise and measurable. Clearly, if we're talking about converting mass into energy, then energy is apparently something other things can be converted into. If mass is a kind of energy, are there other kinds of energy? Can you convert between them too?
Short answer: Yes. (Short answers don't come any shorter than that. Except if the short answer is "no." Which it isn't).
A familiar example of energy conversion is the common roller coaster. On the hilltops the coaster is barely moving, whereas down in the valleys there's lots of speed. You can say we "trade" height for speed (and vice versa). More precisely, we trade potential energy for kinetic energy. The former is an energy of position and the latter is the energy of a moving mass. There are formulas we can use to compute potential and kinetic energy given mass, height, and speed. If we did the math, and ignored sneaky things like friction and air resistance, we would find that the roller coaster always had the same amount of energy; it simply changed between potential and kinetic energy. This is true of any system and is a fundamental physics principle known as the conservation of energy.
Note that motion (kinetic energy) of a roller coaster is what gets us up the next hill. This brings us to the textbook definition of energy: "the capacity to do work." However, we prefer a more graphic definition: the capacity to break stuff.
Consider an example: Hold an egg in your hand. Drop it. The egg hits the floor and breaks.
When the egg was in your hand, it had potential energy by virtue of you holding it up against gravity. When you released the egg, it lost potential energy but gained kinetic energy. When the egg hit the floor, it converted its kinetic energy into mechanical energy that went into breaking the shell and compressing air molecules to make a "sploit" sound. Additionally, some of its kinetic energy was converted into thermal energy. If you used a sufficiently sensitive thermometer, you could discover that the egg (or, rather, egg debris) was a little warmer after breaking compared to before.
Looking at the overall process, we could say you used potential energy to break the egg.
One more example: Light a firecracker. The fuse burns down, ignites the gunpowder and, bang!, no more firecracker. The thermal energy traveling along the fuse released the chemical energy stored in the molecular bonds of the gunpowder which was converted into mechanical energy (bang), light energy (flash), and thermal energy (heat). Like an energy caterpillar emerging from its energy cocoon to become an energy butterfly.
Potential energy. Kinetic energy. Mechanical energy. Thermal energy. Chemical energy. These and other forms of energy were known before E = mc2 arrived on the scene. The equation describes another kind of energy: it says that mass itself has energy. That mass is energy. This is a new kind of energy, different than the examples we have considered. Releasing this energy radically changed the world, as we shall see.
The Punchline
We have now described the three players that appear in Einstein's equation - the speed of light, mass, and energy. We know that the equation not only tells you that mass and energy are interchangeable, it also gives you a quantitative relation between the two: this much mass is equivalent to that much energy. To figure exactly how much, you take the amount of mass (measure in an appropriate unit) and multiply it times the square of the speed of light (also measured in an appropriate unit).
The energy is not kinetic or potential or chemical or heat. It is energy that is contained in the very fabric of matter. Simply by existing - more properly: by having mass - a thing has energy. How much energy? It's mass times the square of the speed of light.
That is what E = mc2 means.
...How do we coax out mass energy? Read on.

Converting Mass to Energy
If you drop an (unlit) firecracker, you convert its potential energy to kinetic energy, just like an egg. But dropping the firecracker does not release the chemical energy it contains. If we want to release its chemical energy, we must do something else. That something else is lighting the fuse. However, lighting the fuse does not release the firecracker's mass energy. Converting mass to energy also requires something else. Something different. Something new.
We get no help here from Albert. When Einstein published his famous equation in 1905, he didn't describe how you convert mass to energy, he simply pointed out that it was possible. You can't "get the energy out" by burning or grinding or boiling. You can't use any sort of chemical reaction. In fact, when other scientists started thinking about the task, many concluded that energy conversion would never be anything more than an equation. Physics big-shot Ernest Rutherford famously dismissed the large-scale release of such energy as "moonshine." It would take centuries, if ever, to figure it out, and the necessary machine might be as big as the sun.
There the idea might have remained, the secret forever locked away. As fate would have it, the idea of mass-energy equivalence and an interest in atomic physics were emerging just as Europe had lost its mind (again) and World War II was getting underway. And, as pointed out above, while energy can be thought of as the capacity to do work, it is also the capacity to break stuff. In a war-time atmosphere, Einstein's equation suggested a way to construct weapons of unimaginable destructive power.
Even if it was unclear how to construct a weapon exploiting E = mc2, it was clear that whoever built one first would have an overwhelming military advantage. The Nazis had lots of scientist and some of the best laboratories in the world. In response, the allies began a frenzied effort to build a weapon of their own. That crash program was called the Manhattan project, and the weapon it created was the atomic bomb.
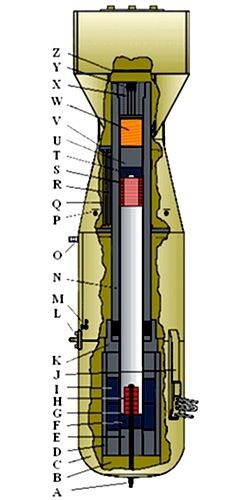
How to Build an Atomic Bomb
A detailed description of how an atomic bomb works is a topic for another day. But we would be cheating you if we didn't at least sketch out the key ideas, as the technology is central to how E = mc2 changed the world.
You may recall the grade-school description of an atom as a miniature solar system, having a nucleus consisting of a "sun" of protons and neutrons packed at the center surrounded by one or more electron "planets" orbiting about. Such a model of the atom is very different from our modern understanding (not to mention, well, wrong) but it will suffice for our purposes.
If we were somehow to split the nucleus - imagine a killer asteroid colliding with the sun of our miniature solar system and breaking it in two - then weigh the debris, we would discover that the sum of the mass of the two parts is less than the mass of the original nucleus.
Where did the missing mass go? It was converted into energy according to E = mc2. Here, then, is how you convert mass into energy: it requires splitting the atom.
In an atomic bomb, the nucleus is split or fissioned using a neutron. In addition to releasing energy, splitting a nucleus also releases a few neutrons. These neutrons find other nuclei to fission, which releases more energy and more neutrons, which then fission more nuclei, and so on. The entire chain reaction takes but a fraction of a second, and even though the energy released in each fission is rather small (approximately enough to make a grain of sand jump), many trillions of fissions occur. As such, the total amount of energy released is enormous. The net results are temperatures hotter than the sun and pressures greater than that at the center of the earth, where iron flows as a liquid.
This brief description glosses over about eleventy gazillion engineering details. For example, some materials fission more readily than others - uranium and plutonium being the two easiest. Only a certain type of uranium will work in a bomb, often separated using a centrifuge, a term that pops up in the news from time to time. You must arrange the bomb material so that neutrons hit another nucleus when released rather than just escape into the air, giving us the concept of critical mass. Similarly, you don't want neutrons to be absorbed by impurities, which requires enrichment. You must devise a way to squirt a few neutrons into the bomb precisely when you want to trigger the explosion and not squirt any neutrons when you don't. And the device must hold together long enough to fission a significant amount of the bomb material. If it blows apart too soon, you get a low-yield weapon called a dirty bomb.
These are challenging technical problems that required a great deal of ingenuity to solve. But at the heart of an atomic bomb - the concept that makes it possible - is mass-energy conversion. A small mass of uranium or plutonium is converted into a tremendous quantity of energy. That process is described by a simple equation, Einstein's famous E = mc2.
The Trinity Test
Here is the very first large-scale man-made mass-to-energy conversion, the Trinity test of the bomb design later used on Nagasaki (the type of weapon dropped on Hiroshima was not tested before it was used). The flash of light at the beginning of the detonation marks the mass-to-energy conversion about a pound of plutonium. The subsequent destructive effects - heat and blast - are a tragic exercise in energy conversion. Most of the energy immediately released by fission is kinetic energy; specifically the two fragments of the split nucleus fly apart at high speed. The kinetic energy of the fission fragments is quickly converted to thermal energy as they collide with and thereby heat the surrounding material. Thermal energy is converted to mechanical energy, as hot material rapidly heats the surrounding air which then expands as a shockwave. There are also large quantities of radiation released, both immediately during fission and over the long term as a consequence of radioactive decay.
Postscript
It would be wrong to leave you with the impression that an atomic bomb is the only technology inspired by E = mc2. The birth of nuclear physics may have been a victim of unfortunate timing, but eventually Einstein's equation found application in peaceful technologies and basic research.
If we control a chain reaction so that it proceeds slowly and use the heat produced to make steam and turn a turbine we obtain a nuclear reactor, a technology that gives us everything from submarine engines to commercial power plants. NASA uses a different kind of nuclear reactor to provide electricity on space probes; one is currently powering the Voyager probe that left Earth in 1977. As of this writing, E = mc2 is crossing the heliosheath and is headed for interstellar space.
Einstein's equation also describes the energy released when two nuclei merge together during fusion, which at first glance makes no flippin' sense whatsoever. If energy comes out when you break apart a nucleus, how do you also get energy out when you put it back together? The answer is that whereas heavy elements (like uranium) are used in fission, light elements (like hydrogen) are used in fusion. The nuclear details that result in both processes being net energy producers are summed-up in something called the curve of binding energy.
Fusion is an active area of power research as it promises cheap electricity sans the toxic waste created by fission (and the carbon emissions created by burning fossil fuels). Alas, fusion is proving very difficult to make work. This because of the extreme temperatures needed to get it going, which are more convenient to produce, say, in the sun than in a laboratory. Still, fusion proponents claim their technology will eventually provide a safe and clean alternative to fission-based nuclear power.
Lastly, Einstein's equation finds application in basic research. So far we have considered mass-to-energy conversion, but the reverse conversion of energy-to-mass occurs everyday in physics laboratories. Take two particles - protons, say - and give them lots of kinetic energy by accelerating them to high speed (really high speed, like > 99% of the speed of light). Then, arrange for the protons to crash head-on into each other so that their kinetic energy vanishes. We know that energy must be conserved. What happens?
What happens is that the collision creates a shower of new particles. "Summoned out of thin air" we might say, although the experiments are done in a vacuum. Such energy-to-mass conversion is the bread-and-butter of particle accelerators in places such as SLAC, Fermilab, or CERN. It is the primary experimental tool that physicists use to uncover the fundamental laws of nature.
Learn more on Amazon

Image Credits
Images may have been cropped, color adjusted, or otherwise modified.
Photograph of Einstein at the blackboard is in the public domain. Labeled E=mc2 from Clker.com. Sparkler by Gabriel Pollard and appears under terms of the Creative Commons Attribution-Share Alike 2.5 Generic license. Scale by Jean Poussin and appears under terms of the GNU Free Documentation License. Clipart of roller coaster and firecrackers from Clker.com. Image of Castle Romeo shot is a work of a United States Department of Energy (or predecessor organization) employee, taken or made during the course of an employee's official duties. As a work of the U.S. federal government, the image is in the public domain. Little boy components by Fastfission and released into the public domain.
--
All other weirdness (c) 2012-14 LabKitty Design