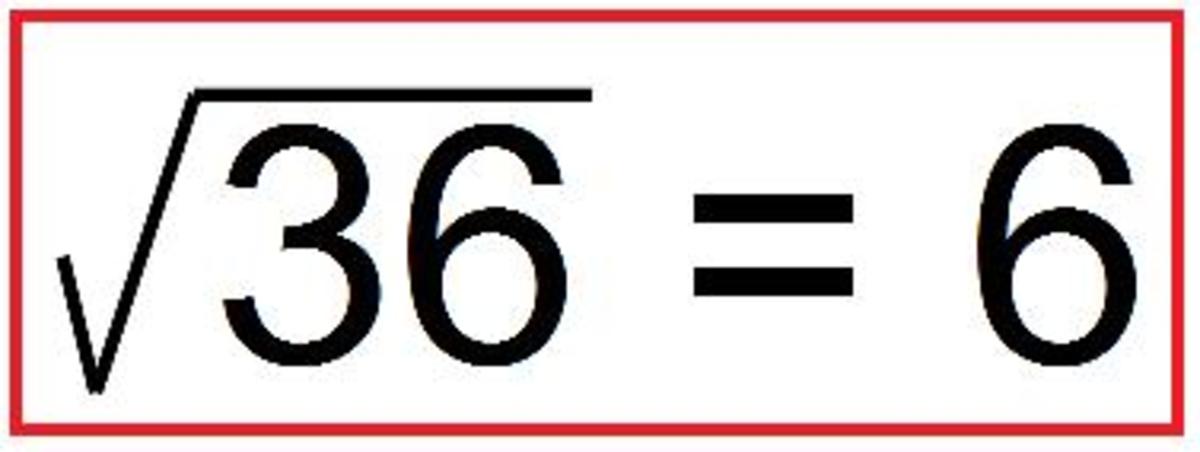How to Figure Square Roots (Reducing)

I am a math tutor. I've been tutoring math since I was in high school back in the last century (well back in the last century). I began in 10th grade tutoring 9th graders in Algebra. The next year, I began tutoring Geometry (my favorite). I also got my first paying tutoring job that year (most of my high school tutoring was volunteer, after school, in the school building).

When I was in college, I tutored high school students in a program called "Upward Bound". I now tutor privately (in my own community) and through an on-line site called "Wyzant".

I bring this up because there are several topics I have noticed trouble my students and I thought this might help them (and other math students) with these subjects (I have other math related lenses).

This is not a lens about using a calculator to find a square root. This is not a lens about finding a square root to its nearest 10th or 100th or 2 places. This is a lens that helps you get from a large number's square root to a smaller number's square root.

In other words, this will show you how to go from ([square root] 20) to (2 ([square root] 5).

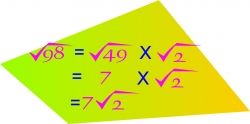
One of the sorts of problems that shows up on Algebra tests is taking a square root of a number that isn't a perfect square (see a list of all the integers that are perfect squares from 1-625 at the bottom of this lens) and reducing it to an easier to handle version. For example, in the picture here, we start with [square root] 98. But, if you notice when you look at the list, 98 is NOT a perfect square.

98, however, equals 2 X 49. 49 is a perfect square -- it's 7 squared (or 7 X 7). So, as you can see in the second step, [square root] 98 = [square root] 49 X [square root] 2. Or, more succinctly, 7 X [square root] 2.

If the number you are trying to divide is one you don't know (as in you can't tell right away by looking at it what perfect square might be a factor), check out Lowest Common Denominator to see how to break numbers into their factors. Or, if the number is low enough, you can look at the list of squares from 1-625 further down in this lens and work from there.

This is a list of the first 25 positive integers with their squares.

1. 1
2. 4
3. 9
4. 16
5. 25
6. 36
7. 49
8. 64
9. 81
10. 100
11. 121
12. 144
13. 169
14. 196
15. 225
16. 256
17. 289
18. 324
19. 361
20. 400
21. 441
22. 484
23. 529
24. 576
25. 625

"Arts Now" is another "Print on Demand" site. They have a nice collection of clocks and watches, including the one pictured here (with math symbols on it). Click on the picture to see the entire math clock collection on the Arts Now site.