- HubPages»
- Technology»
- Computers & Software»
- Computer Science & Programming
How Not to Screw Up Your Models
Introduction
When you are creating models to simulate a process or product, what can you do to not screw up the models? How can you improve the accuracy of simulations and reduce the odds that your data models are completely at odds with reality?
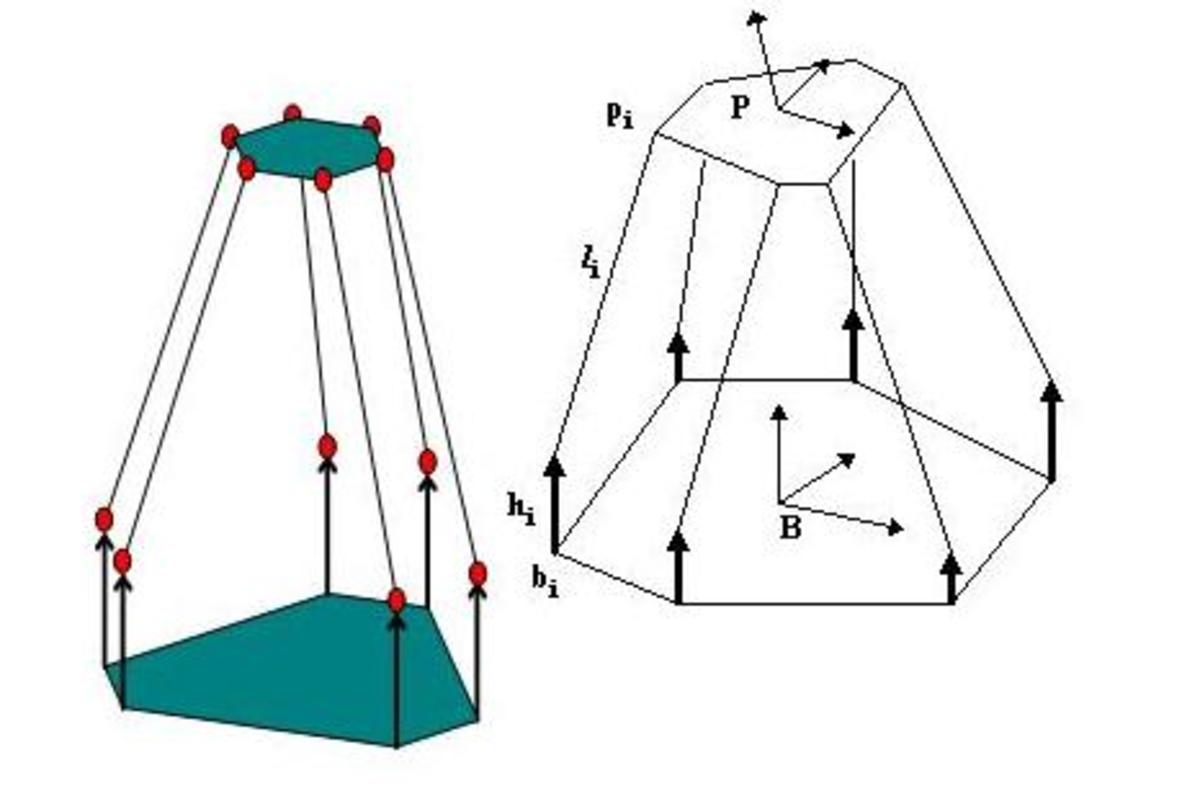
How Not to Mess Up Your Computer Models
Think about the variables that affect the process, such as heat or material quality, not just the process variables like cycle time and human schedules. A model based on a temperature stable environment with heat sensitive materials will be inaccurate when your model doesn’t reflect the actual effects of a hot warehouse and production line.
Compare your model to real world data after the model's been run over time, as you collect real world data as time goes by. Most importantly, if the model doesn't match reality, adjust the model, not the data.
Avoid the temptation to adjust the historical data sets to fit the model, such as throwing out too many outliers or “adjusting” the historic data. Periodic outliers indicate something you aren’t accounting for or provide proof that the process isn’t as neat as your simulation supposes.
The more your data is “treated” or based on estimations and approximations, the more error your model has. For example, temperature data estimated from tree rings and fossil records are not nearly as accurate as temperature from weather stations, no matter how much you want it to be.
Don't get emotionally invested in a model; it is, at best, an approximation of reality.
Running a model off of historic data on which its equations was built doesn’t count as verification except to the degree that if 2+2=4 and 4-2=3.5, you know the model is wrong.
Remember that data trends can often be modeled using different distributions – try different probability distribution types before throwing out the model.
There are always variables you don’t know about.
You can never build a model with all the variables. The complexity of trying to model everything adds more error and uncertainty than a model with the main variables and an understanding that it is 90% to 95% there.
Correlation is not causation.
A really good R-squared doesn’t mean it is correlated, either. One of my professors, Dr. Imrahn, had an excellent presentation linking traffic in California with the population growth of India at the same time. Greater than 95% correlation, but the two trends are obviously unrelated. The website Spurious Correlations by Tyler Vigen has even tightly correlated, unrelated examples.
Recognize that extrapolation is an estimation, when your variable is modeled off data from a small experimental range.
Modeling non-linear systems as linear may be easier and even close to reality, but this may alter other variables so much that the model is useless.
To quote Dr. Pape in my UTA IE program, we have yet to devise a way to soak up variability. Add more variables and you get more uncertainty. Don't assume that adding yet another variable makes the answer more accurate; you just might be more uncertainty in the answer and thus real world data falls within the now wider margin of error.
To borrow from an XKCD joke, physicists like to say you can model anything off some simple process and add another equation to cover the complexities. If your basic model is wrong for the situation, the entire model is wrong.
Recognize that the average result of your models run a thousand times is simply an average of all your educated guesses, and if your assumptions are wrong or the data cherry picked, no more correct than a random guess.
Even data from formal measurements can be off, such as the weather stations that showed significant global warming found to be now surrounded by urban heat islands demonstrated, in contrast to the stable temperatures that still rural weather stations showed.
To quote Kip Hansen, “Nearly all real-world dynamical systems are nonlinear, exceptions are vanishingly rare.” Assuming linear trends makes it easy to project an answer, but that doesn’t make it right when the system is non-linear.

![DataFrameMapper: Delete rows where column[xxx] value is null DataFrameMapper: Delete rows where column[xxx] value is null](https://images.saymedia-content.com/.image/t_share/MjA4MDkzMjY1MTkzMzQ2NzA0/using-dataframemapper-to-delete-rows-where-columnxxx-value-is-null.jpg)
