- HubPages»
- Technology»
- Computers & Software»
- Computer Science & Programming»
- Programming Languages
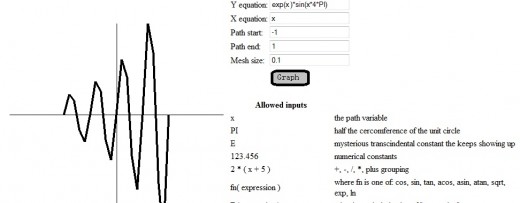
The finished javascript based graphing calculator - part 9 in a series
eploring mathmatical functions - sin(x) in an exponential envelope
discussion of programming issues
Here is the finished javascript graphing calculator. If you have followed this series from the beginning, I have built up from some simple concepts to a somewhat interesting, if basic, application. Well, software is never really done, but this is a logical stopping point for this series. With this series, I have also discussed the usage of most of the javascript "power tools" that I use (loops and conditions, functions, objects, closures, regular expressions, associative arrays, etc ) I haven't discussed javascript libraries which is an important topic of itself, but perhaps that is worthy of its own series of hubs.
This hub does include a couple new concepts. I use an associative array to enforce what is acceptable in an equation to be graphed, and also to simplify the expressions the user has to write, some. For example allowedFunctions[ "sin" ] maps "sin" to the javascript function "Math.sin". It is often very useful to look up a value using a string as a key.
In general, the user will type in a fairly natural expression like D( sin( 2 * PI * x )), and the parsing code will make sure that the functions envoked are ones I chose to support (ln, exp, pow, sqrt, sin, cos, tan, acos, asin, atan, D, S ), operators ( +, -, /, *, ,), symbolic constants ( PI, E ), literal numeric constants, or "x", the path variable used to calculate the points to be graphed. D is a path derrivative function which I discussed in an earlier hub in this series. S is a path integral function.
It would have saved me a lot of graph paper, if I had had something like this when I was in college.
I parse the querystring of the URL that invoked the javascript calculator. This would make it possible to send someone a link to an equation you wanted them to graph. However, now that I am doing this my security concern about links containing reflected javascript, is also a possibility, but not one to fear now that the parsing code is in place.
Finally, I figured out most of my bugs in parsing regular expressions, and it was a bit of an amature's mistake. The back-slashes in the expressions themselves need to be escaped. (e.g. It is \\s not \s that is required to represent white space.) This tells you I have previously used regular expressions in languages other than javascript. Oh well, there is always something to learn. Using "(" as a literal still crashes the regular expression engine, though. I also moved the drawing of the axis into the function that scales the graphing area. If you graph several functions in sequence, you may see multiple axis drawn as a result; not perfect, but to do otherwise would require knowing all of the functions you want to graph ahead of time. This is quite possible, but if you want the graphing calculator to work this way, please, be my guest and make the changes yourself.
If you just want to use the graphing calculator, I put it up on a web site.
key coding point - associative arrays
var allowedFunctions = new Array();
allowedFunctions[ "E" ] = "Math.E";
allowedFunctions[ "PI" ] = "Math.PI";
allowedFunctions[ "*" ] = "*";
allowedFunctions[ "+" ] = "+";
allowedFunctions[ "-" ] = "-";
allowedFunctions[ "/" ] = "/";
allowedFunctions[ "x" ] = "x";
allowedFunctions[ "cos" ] = "Math.cos";
allowedFunctions[ "sin" ] = "Math.sin";
allowedFunctions[ "tan" ] = "Math.tan";
allowedFunctions[ "acos" ] = "Math.acos";
allowedFunctions[ "asin" ] = "Math.asin";
allowedFunctions[ "atan" ] = "Math.atan";
allowedFunctions[ "exp" ] = "Math.exp";
allowedFunctions[ "ln" ] = "Math.log";
allowedFunctions[ "pow" ] = "Math.pow";
allowedFunctions[ "," ] = ",";
allowedFunctions[ "sqrt" ] = "Math.sqrt";
allowedFunctions[ "" ] = "";
...
if ( allowedFunctions[ match2[1] ] != undefined ) {
neweq += allowedFunctions[ match2[1] ];
} else if ( pat4.exec( match2[1] ) ) {
// term is a constant
neweq += match2[1];
} else {
alert( match2[1] + "is not a supported function, or
constant" )
}
...key coding point - accessing the query string
function loadinputdata()
{
var yfn = getinputparam( "yformula", "x*x" );
var xfn = getinputparam( "xfromula", "x" );
document.forms[ "jg_input" ].elements[ "yformula" ].value = unescape(yfn);
document.forms[ "jg_input" ].elements[ "xformula" ].value = unescape(xfn);
}
function getinputparam( pname, def )
{
var tmpStr, tmpInt, pend, rval;
rval = def;
tmpStr = window.location.search.substring(1);
tmpInt = tmpStr.indexOf( pname );
if( tmpInt != -1 ) {
tmpStr = tmpStr.substr( pname.length + 1 );
pend = tmpStr.indexOf( "&" );
if( pend >= 0 ) {
rval = tmpStr.substr( 0, pend );
} else {
rval = tmpStr;
}
}
return( rval );
}
further reading
- jquery - How can I get query string values in JavaScript? - Stack Overflow
- JavaScript Associative Arrays
Using associative arrays in javascript.
complete source code
<html>
<head>
<title>Javascript based graphing calculator</title>
<style type="text/css" >
.whiterectangle { color: white; background-color: white; z-index: 0;}
.blackrectangle { color: black; background-color: black; z-index: 1;}
.jgdialog { position: absolute; top:0; left:460; z-index:1; }
</style>
<script type="text/javascript" >
var allowedFunctions = new Array();
allowedFunctions[ "E" ] = "Math.E";
allowedFunctions[ "PI" ] = "Math.PI";
allowedFunctions[ "*" ] = "*";
allowedFunctions[ "+" ] = "+";
allowedFunctions[ "-" ] = "-";
allowedFunctions[ "/" ] = "/";
allowedFunctions[ "x" ] = "x";
allowedFunctions[ "cos" ] = "Math.cos";
allowedFunctions[ "sin" ] = "Math.sin";
allowedFunctions[ "tan" ] = "Math.tan";
allowedFunctions[ "acos" ] = "Math.acos";
allowedFunctions[ "asin" ] = "Math.asin";
allowedFunctions[ "atan" ] = "Math.atan";
allowedFunctions[ "exp" ] = "Math.exp";
allowedFunctions[ "ln" ] = "Math.log";
allowedFunctions[ "pow" ] = "Math.pow";
allowedFunctions[ "," ] = ",";
allowedFunctions[ "sqrt" ] = "Math.sqrt";
allowedFunctions[ "" ] = "";
function loadinputdata()
{
var yfn = getinputparam( "yformula", "x*x" );
var xfn = getinputparam( "xfromula", "x" );
document.forms[ "jg_input" ].elements[ "yformula" ].value = unescape(yfn);
document.forms[ "jg_input" ].elements[ "xformula" ].value = unescape(xfn);
}
function getinputparam( pname, def )
{
var tmpStr, tmpInt, pend, rval;
rval = def;
tmpStr = window.location.search.substring(1);
tmpInt = tmpStr.indexOf( pname );
if( tmpInt != -1 ) {
tmpStr = tmpStr.substr( pname.length + 1 );
pend = tmpStr.indexOf( "&" );
if( pend >= 0 ) {
rval = tmpStr.substr( 0, pend );
} else {
rval = tmpStr;
}
}
return( rval );
}
var jgpointbase = {
x: 0,
y: 0
};
var msize = 0.1;
function jgpoint( ) {
this.prototype = jgpointbase;
//this.x = x;
//this.y = y;
};
function jgptsc( x, y ) {
var rval = new jgpoint( );
rval.x = this.screenx0 + (( this.screenx1 - this.screenx0 ) / ( this.x1 - this.x0
)) * ( x - this.x0 );
rval.y = this.screeny0 + (( this.screeny1 - this.screeny0 ) / ( this.y1 - this.y0
)) * ( y - this.y0 );
return( rval );
}
var jgcoordinatesbase = {
x0: -1.25,
screenx0: 50,
y0: -1.25,
screeny0: 450,
x1: 1.25,
screenx1: 450,
y1: 1.25,
screeny1: 50,
pointToScreenCoordinates: jgptsc,
scaleToCurve: function ( curvefn, fnstart, fnstop, delta ) {
var pt;
var fofpt;
// get maximum and minimum x and y values
fofpt = curvefn( fnstart );
var minx = fnstart;
var miny = fofpt.y;
var maxx = fnstop;
var maxy = fofpt.y;
for( pt = fnstart + delta ; pt < fnstop; pt += delta ) {
fofpt = curvefn( pt );
if( fofpt.y > maxy ) {
maxy = fofpt.y;
}
if( fofpt.y < miny ) {
miny = fofpt.y;
}
}
var aspectratio = ( this.y1 - this.y0 ) / ( this.x1 - this.x0 );
if( this.y0 < miny ) {
miny = this.y0;
}
if( this.y1 > maxy ) {
maxy = this.y1;
}
if( this.x0 < minx ) {
minx = this.x0;
}
if( this.x1 > maxx ) {
maxx = this.x1;
}
var newaspectratio = ( maxy - miny ) / (maxx - minx );
if( newaspectratio > aspectratio ) {
// match y values and scale x values
this.y0 = miny;
this.y1 = maxy;
var xlength = 1 / aspectratio * ( maxy - miny );
this.x0 = minx + (maxx - minx) / 2 - xlength / 2;
this.x1 = minx + (maxx - minx) / 2 + xlength / 2;
} else {
// match x values and scale y values
this.x0 = minx;
this.x1 = maxx;
var ylength = aspectratio * ( maxx - minx );
this.y0 = miny + (maxy - miny) / 2 - ylength / 2;
this.y1 = miny + (maxy - miny) / 2 + ylength / 2;
}
if ( this.x0 < 0 && this.x1 > 0 ) {
var yaxis1 = this.pointToScreenCoordinates( 0, this.y1 );
var yaxis0 = this.pointToScreenCoordinates( 0, this.y0 );
drawline( 1, yaxis0.x, yaxis0.y, yaxis1.x, yaxis1.y );
}
if( this.y0 < 0 && this.y1 > 0 ) {
var xaxis1 = this.pointToScreenCoordinates( this.x1, 0 );
var xaxis0 = this.pointToScreenCoordinates( this.x0, 0 );
drawline( 1, xaxis0.x, xaxis0.y, xaxis1.x, xaxis1.y );
}
}
};
function jgcoordinates() {
}
jgcoordinates.prototype = jgcoordinatesbase;
function drawrectangle( myclass, top, left, width, height )
{
var bodylist = document.getElementsByTagName( "body" );
var rect = document.createElement( "div" );
var mystyle = 'position:absolute;top:' + top + ";left:" + left + ';width:' + width +
";height:" + height;
rect.setAttribute( "class", myclass );
rect.setAttribute( "style", mystyle );
bodylist[0].appendChild( rect );
}
function drawline( width, x1, y1, x2, y2 )
{
var x, y, nexty, nextx;
x1 = Math.round( x1 );
y1 = Math.round( y1 );
x2 = Math.round( x2 );
y2 = Math.round( y2 );
// ensure x1, y1 is leftmost point
if( x1 > x2 ) {
tmp = x2;
x2 = x1;
x1 = tmp;
tmp = y2;
y2 = y1;
y1 = tmp;
}
var dx = x2 - x1;
var dy = y2 - y1;
if( dy == 0 ) { // horizontal line
drawrectangle( "blackrectangle", y1 - width / 2, x1, dx, width );
return;
} else if ( dx == 0 ) { // vertical line
if( dy < 0 ) {
y1 = y2;
dy = -dy;
}
drawrectangle( "blackrectangle", y1, x1 - width / 2, width, dy );
return;
}
var slope = dy / dx;
if( slope > 1 || slope < -1 ) {
// one x per multiple y
if( y1 < y2 ) {
y = y1;
for( x = x1 ; x < x2 ; x += 1 ) {
nexty = y + slope;
drawrectangle( "blackrectangle", y, x - width / 2, width, nexty - y
);
y = nexty;
}
} else {
y = y1;
for( x = x1 ; x < x2 ; x += 1 ) {
nexty = y + slope;
drawrectangle( "blackrectangle", nexty, x - width / 2, width, y -
nexty );
y = nexty;
}
}
} else {
// one y per multiple x
if( y1 < y2 ){
x = x1;
for( y = y1 ; y < y2 ; y += 1 ) {
nextx = x + 1 / slope;
drawrectangle( "blackrectangle", y - width / 2, x, nextx - x, width
);
x = nextx;
}
} else {
x = x2;
for( y = y2 ; y < y1 ; y += 1 ) {
nextx = x + 1 / slope;
drawrectangle( "blackrectangle", y - width / 2, nextx, x - nextx,
width );
x = nextx;
}
}
}
}
function jgcircle( angle ) {
var rval = new jgpoint();
rval.x = Math.cos( angle );
rval.y = Math.sin( angle );
return( rval );
}
function jgcos1overx2( x ) {
var rval = new jgpoint();
rval.x = x;
rval.y = Math.cos( 1 / ( x * x ) );
return rval;
}
function jgptdiff( fn, x, delta ) {
var rval = new jgpoint();
rval.x = x;
rval.y = -( fn( x ).y - fn( x + delta).y) / ( delta );
//bit of a hack to keep the integration function from reseting
return( rval );
}
function jgdiff( fn, delta ) {
var rval = function( x ) {
return jgptdiff( fn, x, delta );
}
return rval;
}
function jgptint( fn, x, delta ) {
var rval = new jgpoint();
rval.x = x;
rval.y = fn( x - delta ).y * delta;
return( rval );
}
function jgint( fn, delta ) {
var sum = 0;
var lastx = 1000;
var rval = function( x ) {
if( x < lastx ) {
// assume new integral, reset
sum = 0;
} else {
delta = x - lastx;
}
var pt = jgptint( fn, x, delta );
sum += pt.y;
pt.y = sum;
lastx = x;
return( pt );
}
return rval;
}
function xsquared( x ) {
var rval = new jgpoint();
rval.x = x;
rval.y = x * x;
return( rval );
}
function drawcurve( curvefn, coord, fnstart, fnstop, delta ) {
var pt;
var fofpt;
var screenpt, newscreenpt;
fofpt = curvefn( fnstart );
screenpt = coord.pointToScreenCoordinates( fofpt.x, fofpt.y );
for( pt = fnstart + delta ; pt < fnstop ; pt += delta ) {
fofpt = curvefn( pt );
newscreenpt = coord.pointToScreenCoordinates( fofpt.x, fofpt.y );
if( screenpt.x != newscreenpt.x || screenpt.y != newscreenpt.y ) {
drawline( 4, screenpt.x, screenpt.y, newscreenpt.x, newscreenpt.y );
screenpt = newscreenpt;
}
}
}
function makefn( formula ) {
var rfn = function( x ) {
var rval = eval( formula + ";" );
return rval;
}
return rfn;
}
function makepathfn( xfn, yfn ) {
var rfn = function ( t ) {
var pt = new jgpoint();
pt.x = xfn( t );
pt.y = yfn( t );
return( pt );
}
return rfn;
}
function diff( exp ) {
var xfn = makefn( "x" );
var yfn = makefn( exp );
var pfn = makepathfn( xfn, yfn );
var dfn = jgdiff( pfn, msize );
var rfn = function ( x ) {
var pt = dfn( x );
return( pt.y );
}
return( rfn );
}
function integrate( exp ) {
var xfn = makefn( "x" );
var yfn = makefn( exp );
var pfn = makepathfn( xfn, yfn );
var dfn = jgint( pfn, msize );
var rfn = function ( x ) {
var pt = dfn( x );
return ( pt.y );
}
return( rfn );
}
var integratex = integrate( "x" );
var differentiatex = diff( "x" );
var generatedfn = Array();
var gencount = 0;
function parseeq( eq ){
var pat = new RegExp( "^\\s*([a-zA-Z0-9._]+)\\s*(\\S?)(.*)");
var pata = new RegExp( "^\\s*(\\S?)(.*)" );
//var pat = new RegExp( "\s*([a-zA-Z0-9\._]+)\s*([+*/\-\x28\x29])(.*)");
var pat2 = new RegExp( "\\s*([^\\s])(.*)");
var pat3 = new RegExp( "([a-zA-Z0-9._])" );
var pat4 = new RegExp( "[0-9]*\\.?[0-9]*" );
var neweq = "";
var match;
var match2;
var rval = Array();
var subeq;
var oplist = ")-+*/,";
var op,term;
var lasteq ="";
while( eq.length > 0 && eq != lasteq ) {
lasteq = eq;
//check for bare paren
match = pata.exec( eq );
if( match && match[1] == "(" ) {
match[3] = match[2];
match[2] = match[1];
match[1] = "";
} else {
match = null;
}
if( !match ) {
match = pat.exec( eq );
}
if ( !match || match.length < 1 || match[2] == "" ) {
// could be the last term
match2 = pat3.exec( eq );
if( match2 ) {
if ( allowedFunctions[ match2[1] ] != undefined ) {
neweq += allowedFunctions[ match2[1] ];
} else if ( pat4.exec( match2[1] ) ) {
// term is a constant
neweq += match2[1];
} else {
alert( match2[1] + "is not a supported function, or
constant" )
}
} else if ( eq.indexOf( ")" ) >= 0 ) {
neweq += ")";
} else {
alert( "Bad syntax: " + eq );
}
rval[0] = neweq;
rval[1] = "";
return( rval );
}
term = match[1];
//alert( term );
if( match[2] == "" ) {
// make the re work the way I want
match[2] = match[3].charAt(0);
match[3] = match[3].substr(1);
}
op = match[2];
if( op != "(" ) {
if ( allowedFunctions[ term ] != undefined ) {
neweq += allowedFunctions[ term ] + op;
} else if ( pat4.exec( term ) ) {
// term is a constant
neweq += term + op;
} else {
alert( term + "is not a supported function, or constant" )
}
}
while( op != "" ) {
if( op == "(" ) {
subeq = parseeq( match[3] );
if( term == "D" ) {
// create path deriviative function, and name it
var fn = diff( op + subeq[0] );
generatedfn[ gencount ] = fn;
// use created name in expression
neweq += "generatedfn[" + gencount + "](x)";
++gencount;
} else if( term == "S" ) {
// create path deriviative function, and name it
var fn = integrate( op + subeq[0] );
generatedfn[ gencount ] = fn;
// use created name in expression
neweq += "generatedfn[" + gencount + "](x)";
++gencount;
} else if ( allowedFunctions[ term ] != undefined ) {
neweq += allowedFunctions[ term ] + op;
neweq += subeq[ 0 ];
} else {
alert( term + " is not a supported function" );
}
// continue with unmatched part
eq = subeq[1];
match2 = pat2.exec( eq );
rval[0] = neweq;
rval[1] = eq;
if( match2 ) {
// first non-white character should be an operator
op = match2[1];
eq = match2[2];
match[3] = eq;
neweq += op;
} else {
op = "";
}
} else if( op == ")" ) {
rval[0] = neweq;
rval[1] = match[3];
return( rval );
} else if( op == "" ) {
// we're done
rval[0] = neweq;
rval[1] = match[3];
eq = "";
op = "";
} else if( oplist.indexOf( op ) ) {
rval[0] = neweq;
rval[1] = match[3];
eq = match[3];
op = "";
} else{
alert( "Bad syntax: " + eq );
rval[0] = "";
rval[1] = "";
return( rval );
}
}
}
return rval;
}
function jggraph( coord ) {
var xformula = document.forms[ "jg_input"].elements[ "xformula" ].value; //"x*x;";
var yformula = document.forms[ "jg_input"].elements[ "yformula" ].value; //"x;";
var eq;
eq = parseeq( yformula );
yformula = eq[0];
var xfn = makefn( xformula );
var yfn = makefn( yformula );
var pfn = makepathfn( xfn, yfn );
var mstart = parseFloat(document.forms[ "jg_input"].elements[ "meshstart" ].value); //;
var mstop = parseFloat(document.forms[ "jg_input"].elements[ "meshend" ].value); //;
var msize = parseFloat(document.forms[ "jg_input"].elements[ "meshsize" ].value); //;
coord.scaleToCurve( pfn, mstart, mstop, msize );
drawcurve( pfn, coord, mstart, mstop, msize );
}
</script>
</head>
<body onLoad="javascript:loadinputdata()" >
<div class="jgdialog">
<form id="jg_input">
<table>
<tr><td>Y equation:</td><td><input name="yformula" value="x*x" /></td></tr>
<tr><td>X equation:</td><td><input name="xformula" value="x" /></td></tr>
<tr><td>Path start:</td><td><input name="meshstart" value="-1" /> </td></tr>
<tr><td>Path end:</td><td><input name="meshend" value="1" /></td></tr>
<tr><td>Mesh size:</td><td><input name="meshsize" value="0.1" /></td></tr>
<tr><td></td><td><img id="start_calc" src="jggraph.jpg" onClick="javascript:jggraph(unitsquare)"
/></td></tr>
</table>
</form>
<table>
<th>Allowed inputs</th>
<tr><td>x</td><td>the path variable</td></tr>
<tr><td>PI</td><td>half the cercomference of the unit circle</td></tr>
<tr><td>E</td><td>mysterious transcindental constant the keeps showing up</td></tr>
<tr><td>123.456</td><td>numerical constants</td></tr>
<tr><td>2 * ( x + 5 )</td><td>+, -, /, *, plus grouping</td></tr>
<tr><td>fn( expression )</td><td>where fn is one of: cos, sin, tan, acos, asin, atan, sqrt, exp,
ln</td></tr>
<tr><td>D( expression )</td><td>take the path derivative of "expression"</td></tr>
<tr><td>S( expression )</td><td>take the path integral of "expression"</td></tr>
<tr><td>pow( expression1, expression2 )</td><td>expression1 is the base, expression2 is the
exponent</td></tr>
</table>
<script type="text/javascript" >
drawrectangle( "whiterectangle", 0, 0, "100%", "100%" ); // make a background rectangle, not
necessary with default browser settings
var unitsquare = new jgcoordinates();
yaxis1 = unitsquare.pointToScreenCoordinates( 1, unitsquare.y1 );
yaxis0 = unitsquare.pointToScreenCoordinates( 1, unitsquare.y0 );
//drawline( 1, yaxis0.x, yaxis0.y, yaxis1.x, yaxis1.y );
yaxis1 = unitsquare.pointToScreenCoordinates( -1, unitsquare.y1 );
yaxis0 = unitsquare.pointToScreenCoordinates( -1, unitsquare.y0 );
//drawline( 1, yaxis0.x, yaxis0.y, yaxis1.x, yaxis1.y );
</script>
</body>
</html>link to my next series
- The finished javascript based graphing calculator - ...
Just an example of how the javascript based graphing calculator may be used. Here is the finished javascript graphing calculator. If you have followed this series from the beginning, I have built up from some...