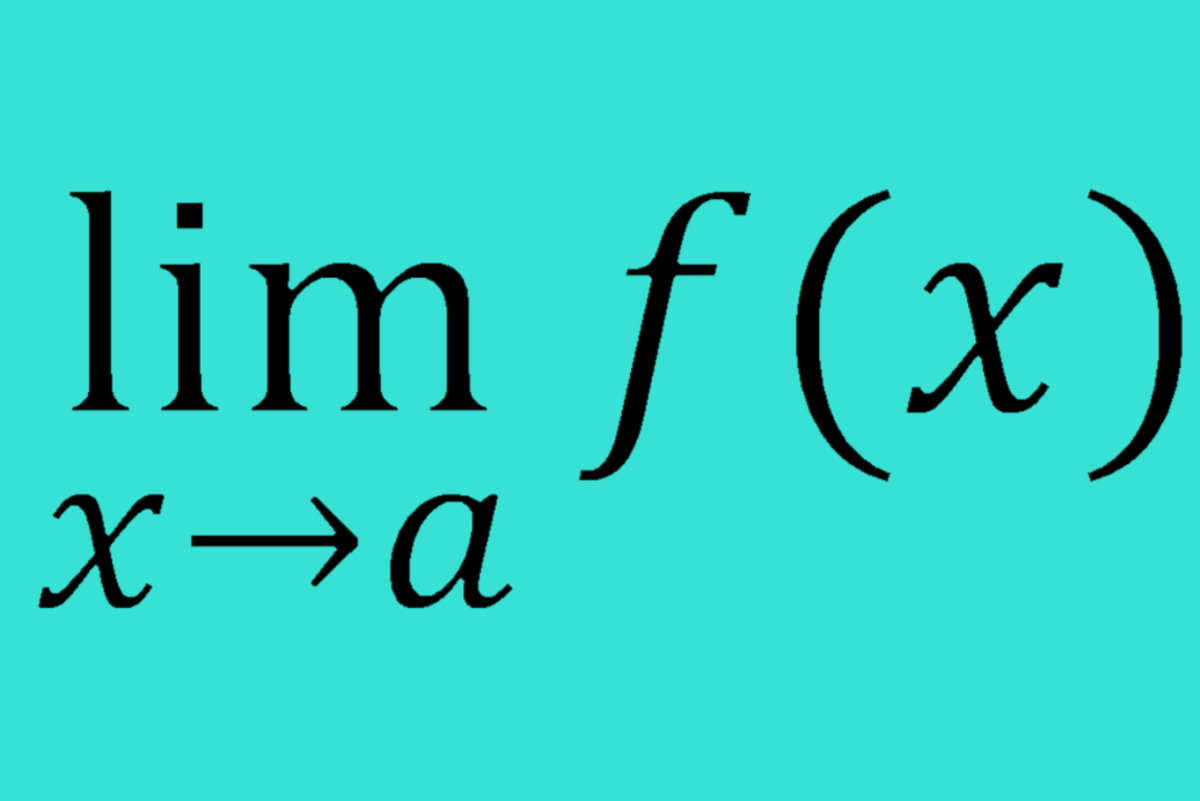How to Find the Area Between Two Curves in Calculus
Finding the area between two curves in calculus is easy. To find the area between two curves, you need to find the area under each curve separately. Then, subtract one from the other to find the difference between them.
Step By Step
How to find the area between two curves in calculus:
- First, you need to find the two points at which the curves intersect. Treat the equations of the two curves as a pair of simultaneous equations for y and x. Solve the simultaneous equations to find two solutions for x.
- Integrate each curve between the two solutions for x that you found in step 1.
- Subtract the smaller value from the larger one to find the area between the curves.
Example
Example: Find the area between the curves y = x and y = x2.
- Find the points at which the curves y = x and y = x2. To do this, substitute y = x for x in y = x2 to get the equation y = y2. This has only two solutions, y = 0 and y = 1. Put these values back into y = x to find the solutions for x. These are x = 0 when y = 0, and x = 1 when y = 1.
- Integrate each curve between x = 0 and x = 1. Use the usual integration rules to integrate each term.
- ∫ x dx = x2 / 2 [at x = 1] - x2 / 2 [at x = 0] = 1/2.
- ∫ x2 dx = x3 / 3 [at x = 1] - x3 / 3 [at x = 0] = 1/3
The difference between the areas under the curves = 1/2 - 1/3 = 1/6.
Solution: The area between y = x and y = x2 is 1/6.
Tip!
You can check your answer by plotting the curves on graph paper and counting the squares to estimate the area between them.