How The Lorentz Contraction Results From Time Dilation - A Detailed Calculation

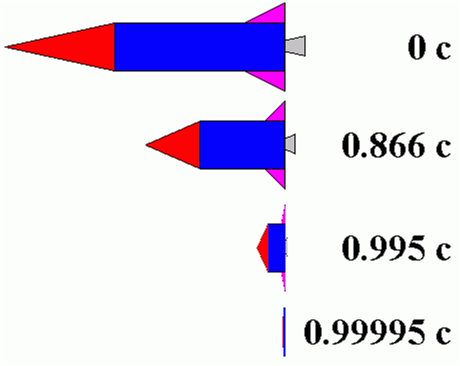
The following calculations show that a direct consequence of the relativistic time dilation phenomenon IS the relativistic distance contraction phenomenon, also known as the Lorentz Contraction. This is just another analogous method of visualizing the distance contraction phenomenon. And in doing so, we revisit the example of the muons, which are created at the very outskirts of our atmosphere, and blaze their way towards a collision with the earth at the very high relative speed of 0.998c. Moreover, we will see (at the end of our calculations) that these two phenomena, namely, time dilation and distance contraction, impose ‘equivalent’ effects on time and space, respectively. The value of the speed of light c is, of course, the universally constant value of 300,000 km/second, or 9.843 x 10⁸ ft/second.

[ 1 ] The muons are moving at a speed of v = 0.998c, relative to us. Thus, calculating this relative speed in units of feet per second gives:

v = 0.998 x (9.843 x 10⁸ ft/second) = 9.823 x 10⁸ ft/second.

[ 2 ] Due to relativistic time dilation, we will observe that their clocks (if the muons were somehow able to carry clocks with them!) are ticking at a slower rate than our clocks by the factor

which is, as we know, the relativistic time dilation factor. Plugging in the numbers, then, we find that we observe that the muons’ clocks are ticking at a rate that is:

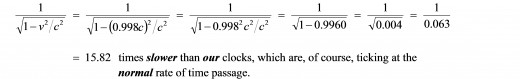
Hence, as observed from our point of view (standing here on earth), the rate at which time itself passes for the muons is 15.82 times slower than the normal rate at which time passes for us!

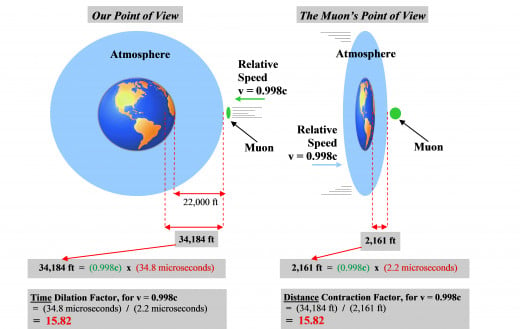
[ 3 ] Furthermore, we also observe that the muons traverse the entire 34,184 feet of normal distance – that is to say, the normal distance of our atmosphere and earth that is measured by us using our rulers – before finally disintegrating (because the muons actually penetrate the earth’s crust).

[ 4 ] Now, since

TRAVEL TIME = DISTANCE TRAVELED / SPEED OF TRAVEL,

then the amount of time that it takes the muons – as observed from our point of view, that is, as measured by us using our clocks – to travel this normal distance thus equals:

(34,184 ft) / v {where v is, of course, the relative speed of the muons}, which then equals:

(34,184 ft) / (9.823 x 10⁸ ft/second), or 34.8 x 10^-6 seconds, which is 34.8 microseconds.

Therefore, as observed from our point of view, it takes the muons 34.8 microseconds of our normal time to travel our measured normal distance of 34,184 feet.

[ 5 ] But, due to the time dilation phenomenon, we observe a corresponding lesser amount of time of only

elapse on the muons’ clocks, during this journey! We will call this amount of time Δt_MUONS. And so, carrying this calculation through gives us:

We note here that the value for the amount of time Δt_MUONS could have just as easily been calculated by multiplying the 34.8 microseconds that elapse on our clocks (during the muons’ journey) by the quantity 1 / 15.82 (which is, as we know, the inverse of the time dilation factor), because we have already calculated that we will observe the muons’ clocks ticking 15.82 times slower than our clocks. That is to say, we have already calculated the time dilation factor to be equal to 15.82. Hence, carrying this calculation through gives us:

To recap, from our point of view, we observe a time interval of 34.8 microseconds elapse on our clocks during the muons’ 34,184 ft journey, but we observe a corresponding lesser time interval of only 2.2 microseconds elapse on the muons’ clocks during this journey! That is, from our point of view, the muons’ clocks are ticking in slow motion, specifically:

(34.8 microseconds) / (2.2 microseconds), or 15.82 times slower

than our clocks, which are, of course, ticking at the normal rate of time passage!

[ 6 ] Now, since

DISTANCE TRAVELED = SPEED OF TRAVEL x TRAVEL TIME,

then, from the muons’ point of view, since it only takes Δt_MUONS, namely, 2.2 microseconds, of normal time for the earth (which is, of course, moving at the relative speed of 0.998c) to reach them, they will ‘measure’ a travel distance of only

(9.823 x 10⁸ft/second) x (2.2 x 10^-6seconds), or only 2,161 ft!

Hence, the muons will ‘see’ the full 34,184 ft distance to be contracted, or compressed, into a distance of only 2,161 ft along the direction of relative motion! Consequently, the muons will ‘see’ a travel distance that is

(34,184 ft) / (2,161 ft), or 15.82 times shorter

than the travel distance we see!

Therefore, the fact that time is dilated by a factor of 15.82 for the (relatively) moving muons directly results in the muons “seeing” a travel distance that is contracted by a factor of 1 / 15.82 along the direction of relative motion. That is to say, the distance contraction phenomenon is a direct result of the time dilation phenomenon. The following diagram will help to illustrate this fact (we note here that due to the symmetry of special relativity, we will observe the muon itself - that is, its diameter - to be also contracted along the direction of motion!).

And finally, we can summarize this example using a purely algebraic form, as follows:

[ 1 ] First, we observe a muon moving at the speed v, relative to us.

[ 2 ] We observe that the muon’s clock is running slower than our clock by a factor of

[ 3 ] Furthermore, we also observe that the muon traverses the entire normal distance – that is to say, the normal distance of our atmosphere and earth that is measured by us using our rulers – before finally disintegrating (because the muon actually penetrates the earth’s crust). We will call this normal distance L₀.

[ 4 ] Now, since

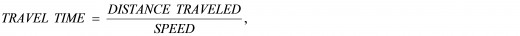
then, from our point of view, i.e., as measured by our clock, the amount of time that it takes the muon to travel the normal distance, L₀ , is equal to

[ 5 ] But, due to the time dilation phenomenon, we observe a corresponding lesser amount of time of only

elapse on the muon’s clock, during this trip.

[ 6 ] Now, since

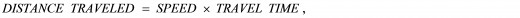
then, from the muon’s point of view, i.e., as “measured” by the muon using its rulers, the muon therefore “sees” a contracted travel distance, L_C, which is given by the expression:

To summarize what this equation is saying, then: From the muon’s perspective, it “sees” the full normal distance, L₀, to be contracted, or compressed, into a shorter distance, L_C, by a factor of