Regiomontanus

The most influential mathematician of the fifteenth century was Johann Müller. Müller was born in 1436 in the German village of Unfinden, which is now part of Königsberg, Bavaria, and he is generally known by the Latinized form of his birthplace, Regiomontanus.

Regiomontanus studied first at the University of Leipzig, and then under Georg von Peurbach in Vienna where he completed the latter’s translation of Ptolemy’s Almagest , as well as making his own translations of works by Archimedes, Apollonius and Heron.

Regiomontanus’ greatest work was his treatise De triangulis omnimodis , written in 1464 but not printed until 1533, several years after his death. De triangulis was the first systematic exposition of plane and spherical trigonometry treated independently of astronomy written by a European. It is divided into five books: the first two on plane trigonometry give a systematic account of methods for solving triangles including the Law of Sines, and the other three on spherical trigonometry. On many occasions he used rhetorical algebra to solve problems.

Another tract on trigonometry Tabulae directionum was also published posthumously in 1490.

Regiomontanus travelled widely in Germany and Italy, but later settled in Nuremberg where he established an observatory and wrote some tracts on astronomy which he printed on his own press. He also made a mechanical eagle that flapped its wings.

Regiomontanus died in suspicious circumstances in 1476 when working in Rome on the reformation of the calendar. Some accounts say he was poisoned.

A contribution of Regiomontanus to mathematics

The following is an adaptation of Book II, proposition 23 of De triangulis omnimodis .

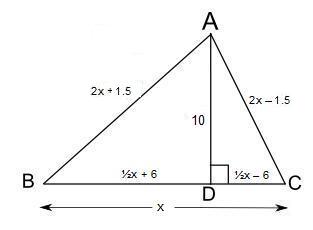
The sides AB and AC of a triangle ABC differ by 3 units. The perpendicular from A onto BC meets BC at D. AD is 10 units and the difference between BD and DC is 12 units.

Solve the triangle.

Regiomontanus used syncopated algebra and worked in Latin, but what follows using modern algebra in English is essentially the method he followed.

Because the difference between BD and DC is four times the difference between AB and AC, it follows that the sum of AB and AC is four times the sum of BD and DC.

Therefore, if the length of BC is x:

1. BD + DC = x

and, since the difference between BD and DC is 12 units, then they must be

½x + 6 and ½x – 6 respectively.

2. AB + AC = 4x

And, since the difference between AB and AC is 3, then they must be 2x + 1.5 and 2x – 1.5 respectively.

Hence the diagram looks like this:

Now use Pythagoras’ Theorem in one of the two right-angled triangles.

It doesn’t matter which, so I will use triangle ABD.

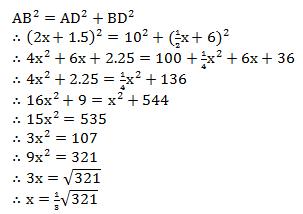
This is the same result as that obtained by Regiomontanus.

Unfortunately this result gives a negative value for the length of DC, which means D should be outside the base BC. It’s not clear whether or not Regiomontanus was aware of this.