How to Add Fractions in Five Easy Steps
Easy Method to Add Fractions
Adding fractions can seem an impossible challenge. How can you add something as different as, for example, thirds (1/3) and sevenths (1/7)? That is the crux of the problem. The key to conquering the addition of fractions, is to realize that you need to first make the fractions compatible (by finding a common denominator). Then you need a dependable, easy method to make the fractions compatible. This article will walk you through some examples and also includes a video demonstration. For best results, I would recommend reading this article and then watching the video (see link to YouTube video, below).
There's an added bonus, the technique for adding fractions is virtually identical to the technique for subtracting fractions.
Video: How To Add Fractions in Five Easy Steps
Terminology
Half (or is it five-eighths?) the battle with fractions is knowing the terminology. Here are some basics:-
Mixed Number = 1¼ - i.e a mixture of a whole number and a fraction.
Improper number = 5/4 - i.e a fraction where the top number (the numerator) is greater than the bottom number (the denominator).
Numerator and Denominator Defined:-

Related Math Hubs
- How to Multiply Fractions in Four Easy Steps
This article shows you how to multiply fractions in four easy steps. How do you multiply mixed numbers? What is an improper fraction? This article, which includes a short video, will answer all these questions and leave you with the knowledge and con - How to Subtract Fractions in 5 Easy Steps
Subtracting one fraction from another is easy when you know how! This article uses an example to show the 5 easy steps. Including converting mixed numbers to improper fractions and finding a common denominator - How to Learn Times Tables Fast
Lots of tricks and tips to make the learning of times tables right up to 10 x 10 faster and more fun. - Primary School Maths
I was intrigued to find out how numeracy is taught at my sons's primary school. I'd heard that the traditional methods that I had been taught had been replaced by a number of different techniques to teach addition, subtraction, division and multiplic
Example: Add 1¼ + 3/7
As with all math and numeracy lessons, the best way is to use an example. Here are the 5 easy steps to add 1¼ + 3/7
Step 1 Convert Any Mixed Number to an Improper Fraction
Example 1¼ + 3/7
In this example 1¼ is a mixed number. Before we can complete the addition we need to convert this mixed number into an improper fraction (remember an improper fraction is one where the numerator is greater than the denominator). To convert a mixed number into an improper fraction multiply the whole number by the denominator of the fraction (in this case 1 x 4) and add to the numerator of the fraction (in this case 1). This gives a new numerator to place over the denominator:-
1¼ - Numerator = (1 x 4) + 1 = 5. Denominator = 4. Improper fraction = 5/4.
So 1¼ + 3/7 becomes 5/4 + 3/7
Step 2 Find A Common Denominator
Again using our example 1¼ + 3/7 = 5/4 + 3/7.
So we need to find a common denominator for 5/4 + 3/7. For more straightforward fractions, you may just know the common denominator. However we need a foolproof method that will work with the addition of any fractions. All we need to do is multiply the existing denominators, in our example denominators are 4 and 7, so we know that a common denominator will be:
4 x 7 = 28
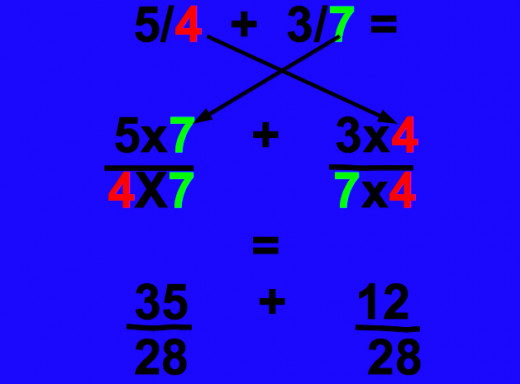
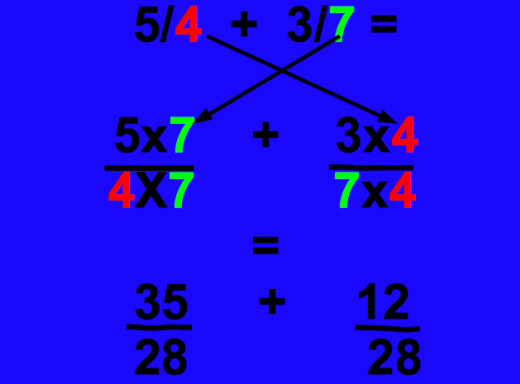
Step 3 Convert the Numerators
Multiply the numerators by the same amount you multiplied the denominators:-
1¼ x 3/7 = 5/4 x 3/7 =
(5 x 7)/(4 x 7) + (3 x 4)/(7 x 4) =
35/28 + 12/28
To be honest this is the most difficult part to do (and to explain!) - look at the illustrated example here and answer a few questions yourself and it will soon become second nature.
Step 4 Add The Numerators
First a recap:-
Step 1 = 1¼ + 3/7 = 5/4 + 3/7
Step 2 = Common denominator = 4 x 7 = 28
Step 3 = 5/4 + 3/7 = 35/28 + 12/28
Step 4 is the easiest part, we just add the numerators:
Step 4 = 35/28 + 12/28 = 47/28
Step 5 Simplify and Convert Improper Fractions back to Mixed Numbers
In reality step 4 gave us an answer BUT depending on how fussy your teacher, or more importantly, your exam board is, you may lose marks for not simplifying fractions or converting improper fractions to mixed numbers. Step 5 is the final step where we tidy our answer up by simplifying, if possible and if we have an improper fraction (i.e. where the numerator is greater than the denominator) converting to a mixed number.
In our case our preliminary answer from step 4 is: 47/28 - this fraction cannot be simplified but it is an improper number so we need to turn into a mixed number. To do this we divide the numerator by the denominator to give the number of whole units. The remainder over the denominator gives the fraction.
In our case 47 ÷ 28 = 1 remainder 19 so our final answer is :-
Final Answer