Primary School Maths
How Numeracy Is Taught at My Son's School
I'd always been intrigued and puzzled by how maths and numeracy is taught at schools. Fortunately my son's primary school has an enlightened policy of explaining to parents the various techniques that they use. I had the opportunity to be shown the methods and the school also issued a small booklet that explained the approach step by step.
I found this information fascinating, useful and a bit of an eye-opener. I thought I would share it and see how my son's school's methods compare to other UK schools and to schools across the world.
Primary School National Maths Strategy/Curriculum
The way maths and numeracy is taught at school seems to continually discussed and revised. Just this month (June 2012), Michael Gove (Secretary of State for Education) unveiled proposals to overhaul the maths/numeracy curriculum. It is proposed that there will be more emphasis on learning specific key tasks. For example 11 year olds will be expected to learn up to their 12 times table (currently the target is up to the 10 times table).
Secretaries of State will come and go, but children will always have to learn how to add, subtract, multiply and divide. This article will focus on how this basic numeracy is taught at my son's school. There is much debate about whether children should learn by rote (for example by chanting their times tables) or by developing a deeper understanding of how numbers work. I'm pleased to say that my son's school use a wide spectrum of strategies to enable all children to achieve success.
My Son's Primary School's Numeracy Strategy
This is an overview taken from a handout:-
"Addition and subtraction, and multiplication and division, are taught alongside each other so that the children can see the relationship between them, recognising that multiplication can be repeated addition and division can be repeated subtraction. Children are also encouraged to understand the importance of estimation and other checking including using inverse operations.
A variety of recording and calculation methods are taught as a progression. However, teachers are flexible in their approach and will realise that some children are ready to progress to the next step and some children will need consolidation on the previous step. This is addressed through appropriately differentiated teaching. It is also important to understand that not all children will reach the final stage in each progression but they will be able to perform a calculation successfully."
So that's the official line. It might be good mathematical practice but it's not plain English! To be fair to the school they also provided examples of how addition, subtraction, multiplication and division is actually taught. I'll set out the approach in detail.
How Addition is Taught at Primary School
This is the progression (starting with the easiest methods) that my son's school follows for addition:
Counting On - Just counting- 11 + 5 = 11, 12, 13, 14, 15, 16. I guess using fingers, or for larger numbers, number lines or squares.
Using a Known Fact - Just learning simple additions. E.g. 3 + 2 = 5.
Number Bonds - Learn which pairs of numbers add up to 10 and 20.
Using a Derived Fact - This builds on a known fact or number bond. For example 15 + 5 = 20, therefore 16 + 5 = 21.
Hundred Squares - A lot easier to understand this with actual examples- check this link, add using a hundred square
Adding Several Numbers - Look for pairs of numbers that add up to 10 and add these first. Children are also taught to start with the largest number. Also children look for pairs that make 9 or 11 and add these by adding 10 and then adjusting by 1.
Partitioning and Recombing Best explained with an example:
85 + 16 = 85 + 15 + 1 = 100 + 1 = 101
Partioning in Tens and Units - Adding the tens up first, followed by the units. For example:-
82 + 25 = (80 + 20) + (2 + 5) = 100 + 7 = 107
I can see how all the previous steps build to this point which in turn leads to the final traditional "Standard Written Method with Exchanging"- see the last step below. There are couple of points that strike me. Firstly it must be painful for bright children to go through all these steps- especially if they have been taught the fundamentals at home. I hope that schools have strategies to avoid such frustration. Secondly it's impossible, when you know how to add up, to fully appreciate the benefit of this step by step approach. Your natural inclination is to be impatient and say why not just teach the final method. I now understand how these steps should allow children of all abilities to build their numeracy skills in a relatively consistent and reliable manner.
Counting on in Multiples of 100, 10 or 1 Here's and example:
86 + 57 = 86 + 50 + 7
86 + 50 = 136 + 4 = 140 + 3 = 143
Adding Significant Digits First An extension of partitioning. Add hundreds, then tens and then units. Children are expected to do these sums in their heads, perhaps with jotted notes to help them
Example:
625+ 48 =
600
60
13
= 673
Adding Near Multiples of 10
Example 527 + 298 = (527 + 300) - 2 = 827 - 2 = 825
Compensation Small extension of previous step
527 + 83 = (527 + 100) -17 = 627 - 17 = 610
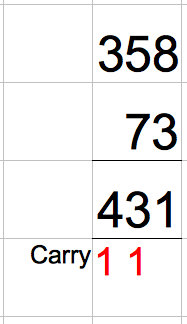
Standard Written Methods with Exchanging
This is the method I remember from school. Adding the units first and carrying below the line, as per this example:-
- How to Subtract Fractions in 5 Easy Steps
Subtracting one fraction from another is easy when you know how! This article uses an example to show the 5 easy steps. Including converting mixed numbers to improper fractions and finding a common denominator - How to Add Fractions in Five Easy Steps
How to add fractions? Adding fractions is not something you can work out for yourself, you need a step by step method. This article walks you through 5 easy steps to add any two fractions and also includes a link to a video with a worked example. - How to Multiply Fractions in Four Easy Steps
This article shows you how to multiply fractions in four easy steps. How do you multiply mixed numbers? What is an improper fraction? This article, which includes a short video, will answer all these questions and leave you with the knowledge and con - How To Study Effectively For Exams And Tests
Many people study hard for exams and tests but how many study effectively? This article considers a number of techniques to make sure you get the most from each hour of studying. - How To Learn Times Tables
How to learn your times tables fast. There are a few tricks to help you with your times tables and even a link to my video