The Shape of Things to Come
Shape up, or Ship Out
Having looked recently at Mathematics - the Science of Patterns , More on the Patterns of Maths , with the previous , Mathematics of Cricket , involving mathematical theories out of a physical game, we can move now into a more geometric oriented world with this particular Hub.
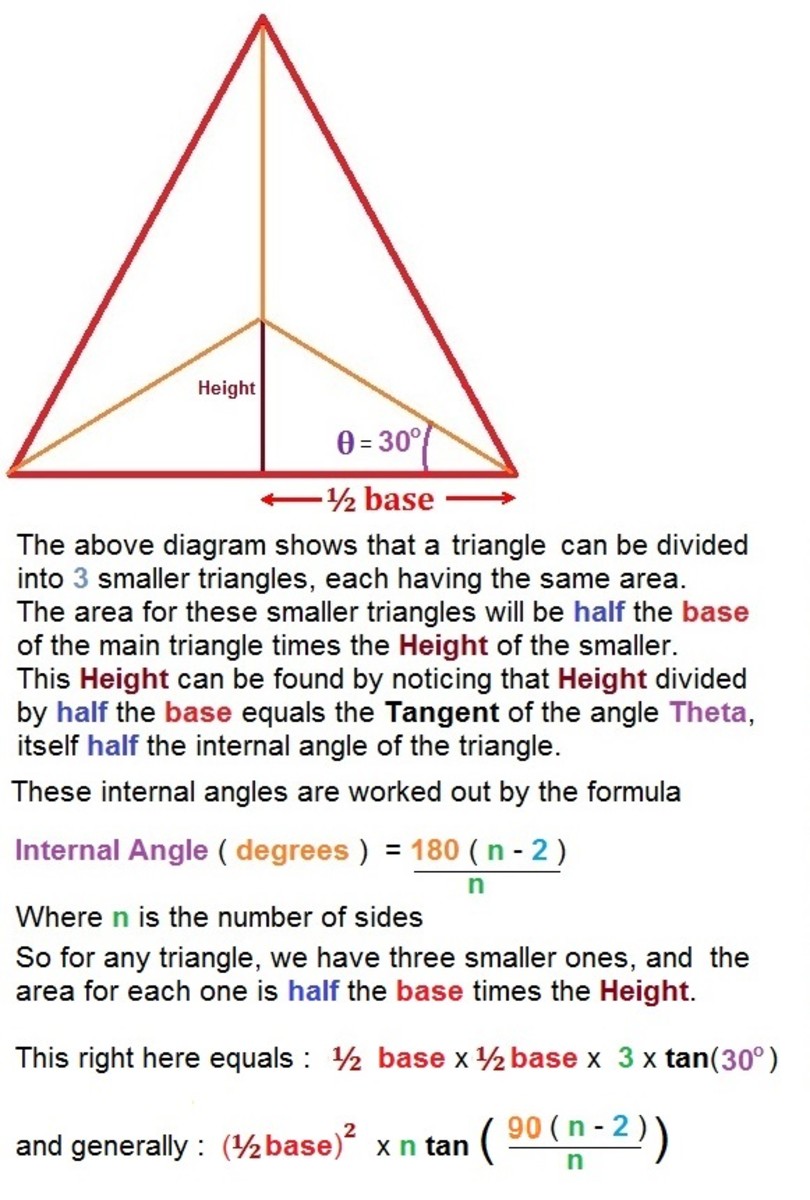
Once in a while you may have been shown an illustration involving certain shapes, and been asked some sort of trick question about it. Take a look at the following diagram on the next page, and tell me how many squares there are :

How many Squares indeed
Now most people would admit at first to saying there are 4 squares there, and of course they forget the outside 2 by 2 square, giving us a total of five. This is simple enough, but what if some clever tool gives you a 10 by 10 square to solve ? How do you know you won’t miss one? Is there an algorithm or even a formula possible for determining how many squares there might be in tricky situations such as this ?
Checking different Arrays of Squares for Patterns
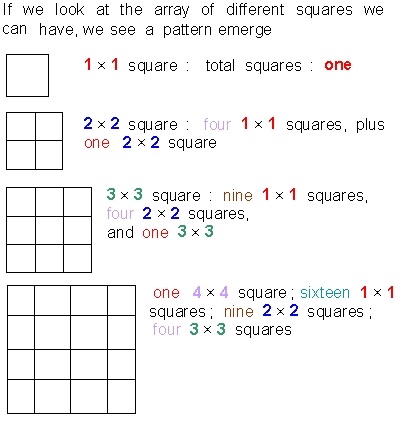
How 2 x 2 Squares can be counted on the 4 x 4
Looking at the 4 by 4
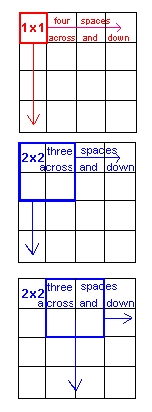
For the 4 by 4, if we count the 1 × 1 squares, we can count each one, then move one space along the row to the next one, with four in all in the row, and four in each column for a total of 16. But if we try 2 × 2, because they are larger, on each row and column we see one less space to move in either direction, so we only get to move 3 across in each direction.
This is true even though the squares overlap, giving us only 3 such squares that way instead of 4 when counting the one by one. So in total we get only nine. Then with the 3 × 3, because they take up even more space, they leave less space to move, so you count one square, taking up three spaces each way, and find you are left with only one space left on the row in the 4 by 4 square specifically to move the overlapping square to count, and then the same downwards, and so on.
See the illustration on the right to understand what I mean. For the 2 by 2 example, only two situations are shown, because I think You can all get the idea, by imagining the 2 by 2 square being able to slide one space along, then another space, as well as two others spaces down.
Getting right down to it
What happens, is that the number of each type or dimension of square ends up being a square, and within a given square, these squares are consecutive, so that we end up with a sum of squares.
For instance, if we look at each square, we see they are comprised of the following :
1 × 1 : 1² squares ; 2 × 2 : 1² + 2² squares ; 3 × 3 : 1² + 2² + 3² squares ; 4 × 4 : 1² + 2² + 3² + 4² squares
Thus we see that squares of successive dimensions add a square value each time, only that the value itself is that of squares of differing dimensions each time. Therefore, the way we see the increase in the number of squares in this kind of pattern, is by the sum of squares formula :
( 2x³ + 3x² + x ) ÷ 6
This means, that if we want to find the total number of squares of various dimensions within a pattern of squares like this, we set its side as x, and go for it.
For example : the total number of squares in the 4 × 4 square, where x = 4, is : ( 2 × 4³ + 3 × 4² + 4 ) ÷ 6, which equals 30, which is indeed the correct answer. So, if someone comes to you with that kind of trick question, and you have remembered this formula, just plug the value of the square’s side in, and you’re it.
Their line is gone out through all the Earth
The same kind of reasoning can be extended to other kinds of shapes, such as lines or cubes. If you had a line with notches in it, and were asked the total number of lines ( or line segments ) there are, your answer can be obtained by the sum to x formula, where the numbers generated are triangular.
For example :
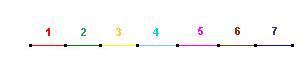
Walk the Line
How many line segments are there in the diagram above ? Obviously, we see it divided into seven sections, each one unit long then we count the long line, seven units in length, but there are also the overlapping ones, as there are with the squares. We can count the parts of the line two units in length, beginning with the one composed of unit lengths one and two, then the next one, slightly overlapping the first, having units two and three, and if we keep counting, we shall realise that there are six of these. Then, if we go on to the line segments three units in length, we can have the first encompassing units one to three, the second from two to four, and if we continue, we find there are five lengths, each 3 units long. When we are finished, we find there to be a total of 28 line segments of varying length, since all we do to find them is find the sum of all numbers from one to seven. Check out the illustration below.
How we count two space line segments along a seven space one
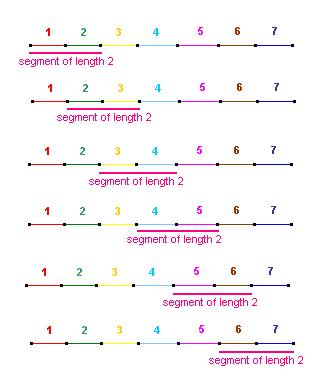
Possibly even in three Dimensions
Now, were we to apply this idea to finding cubes, if we had one large cube of certain dimensions, within which were hid smaller cubes of lesser dimensions, all we do to find the total number of cubes of all sizes combined, is to use the formula for the sum of cubes, and we would be right. This then shows a more practical application of the summation formulae.
Also having three Sides
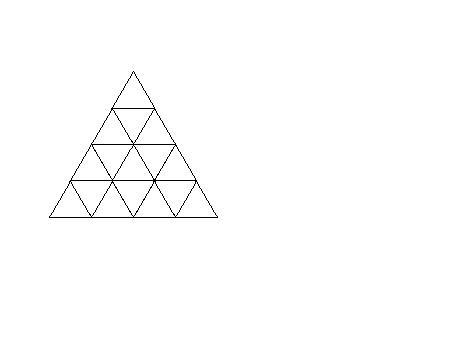
After all of this, you might want a lie down, but there’s still more to consider. Imagine if someone else presents you with the diagram here, and asks you to tell you how many triangles there are, see if you could guess, or would you hope for a formula ?
How we work out the Triangles
We see triangles point up as well as down, and there are patterns also in this way, as well as trying to work out total number. We call this a 4 × 4 triangle, since we have four small triangle bases along the base of the largest. We count 10 upright 1 × 1 triangles, and 6 pointing down. Both 10 and 6 are triangular numbers, or sums.
10 is the sum to 4, 6 the sum to three. The next sized triangle is 2 × 2, which overlap each other. If we count the upright ones we find there to be six of them, but only one downward pointing triangle with dimensions of 2 × 2. This is the last of the downward ones hidden within this larger triangle. There will always be more upward pointing ones, unless we flip the whole thing, but let’s not.
If we continue, we shall find there to be three upward pointing triangles of dimensions 3 × 3, and the last one is the overall 4 × 4. This gives us a total of twenty upward triangles, and seven downward ones, giving us 27. We see that the upward triangles add up to a kind of sum of sums, or sum of triangular numbers, from sum to one, to sum to four : 1 + 3 + 6 + 10 = 20, and the downwards end up being alternate sums, since 6 is the sum to three, while one is of course the sum to one. There is no overall formula for how many triangles there are in total, but rather one for triangles with an odd number side, and another almost identical for triangles with an even number side like our 4 × 4 here. But let us first of all analyse what we have.
Dividing and Conquering
What we can do first is in fact find separate formula for up or down pointing triangles, and then put them together. After much exhaustive trial and error, I discovered that if I take the dimension of the largest triangle, in this case, four, and I sum all the squares from 1² to 4², I get 30. Then I subtract from this ½x, to get 28, then divide this by four, and get seven, this equals the number of down pointing triangles.
If x were odd, after subtracting ½x, I then take away ½ more, before dividing by four. For example, if my triangle is a 3 × 3, it contains only three 1 × 1 down pointing triangles, so if we sum the squares from 1² to 3² to get 14, we take off half x ( which = 1.5 ), then ½ more, a total of two, to give us twelve, which, if we divide by four gives us our three. Let us see how it works when we express what is going on algebraically :
[ ( 2x³ + 3x² + x ) ÷ 6 - ( x ÷ 2 ) ] ÷ 4,
(Just for simplicity’s sake, we are assuming for now that x positive.)
First we need to merge ( x ÷ 2 ) into the same fraction as the preceding, so if we multiply x by three, well, 3x ÷ 6 is the same as saying x ÷ 2, so once we have : [ ( 2x³ + 3x² - 2x ) ÷ 6 ] ÷ 4 ( the 3x was added to the x )
This turns to : ( 2x³ + 3x² - 2x ) ÷ 24, which is then the formula for working out downward pointing triangles on those where x is even. Let’s check :
x = 4 : ( 2 × 4³ + 3 × 4² - 2 × 4 ) ÷ 24 = 7, which is true.
The Odd Couple
But let’s put an odd number in and see what happens x = 3 : ( 2 × 3³ + 3 × 3² - 2 × 3 ) ÷ 24 = 3.125, which obviously is not right. We cannot have a fractional downward pointing triangle. What ? Would that mean we have 3 whole triangles, and one eighth of a side for this to work ?
No, but it is as I alluded to before - there is a separate but almost identical formula for triangles with odd numbered sides. Let us go look again at what happens algebraically, this time when we apply what happens to find downward triangles when the side of the large triangle is odd.
[ ( 2x³ + 3x² + x ) ÷ 6 - ( x ÷ 2 ) - ½ ] ÷ 4
First we need to combine the ½ with the ( x ÷ 2 ), by making it all one fraction of ( x + 1 ) ÷ 2, which is to be all subtracted from the larger part of the equation. Next we alter ( x + 1 ) so we can incorporated into the other fraction, by multiplying it by three, then expanding. Having done that and tidied it up, we end up with the following :
( 2x³ + 3x² - 2x - 3 ) ÷ 24, which differs by the first by only - 3. Shall we see if it works ?
Let x = 3 : ( 2 × 3³ + 3 × 3² - 2 × 3 - 3 ) ÷ 24 = 3, and this is the correct answer.
There really is Strength in Numbers
But since these formulae are for finding just the upside down triangles only, we need to combine it with the one we use to determine how many right side up triangles we have. Now remember, we realised before that the latter are the sum of sums, or alternatively, the sum of consecutive Triangular Numbers. For this I had to work out a formula, and it turns out to be the following : ( x³ + 3x² + 2x ) ÷ 6. Now unlike what we have done before, we do not have to multiply these two formulae together, rather all we do is add them, and to do so, we simply multiply everything within the parentheses by four,
( x³ + 3x² + 2x ) ÷ 6 = ( 4x³ + 12x² + 8x ) ÷ 24, then add them together : ( 6x³ + 15x² + 6x ) ÷ 24, for even sides, and : ( 6x³ + 15x² + 6x - 3 ) ÷ 24, for odds, both of which can be reduced down to ( 2x³ + 5x² + 2x ) ÷ 8, and ( 2x³ + 5x² + 2x - 1 ) ÷ 8.
x = 4 : ( 2 × 4³ + 5 × 4² + 2 × 4 ) ÷ 8 = 27, is correct
x = 3 : ( 2 × 3³ + 5 × 3² + 2 × 3 - 1 ) ÷ 8 = 13, too right
Then the only concern with the number of triangles in such a puzzle, is whether or not the sides are odd or even. Of course you could use the even formula for both, then subtract any fractions, and you will get your correct answer.
Disclaimer
Even though some of this Hub contains certain Mathematical knowledge that can be accessed in the public domain, and therefore is not subject to any Copyright, other information has been drawn from textbooks which themselves are Copyright, but only in the sense of how they deliver the information which itself is shared and sometimes ancient Mathematical knowledge. Other information has also been found on Wikipedia ( Copyright 2013, the Wikimedia Foundation ), which is a good source of information. Part of this is also my own discovery, but may also independently have been found by others. Some titles are common quotes like shape up or ship out, and a paraphrase of the common divide and conquer.
All illustrations in this particular Hub are my own, and have primarily been done using Microsoft™ Paintbox, and Microsoft™ Word. As far as I know, the concept of the formula for shapes within shapes as shown above is mine, but the idea of having say a two by two square, but realizing there are five squares in such an illustration may have come from those old matches tricks, where one lays matches down in a pattern and asks one how many squares there are.
The quote " Their line is gone out through all the earth " , is from Psalm 19 : 4, and always, my Bible quotes come only from the Authorised King James ( 1611, 1769 ) Bible.
The Title " The Shape of Things to Come " is a play on the word shape for its multiple meanings, and was originally the Title of a 1933 Science Fiction work by H.G. Wells ( 1866 - 1946 ), as an indication of what the History of the Future ( our time also ) might be like. This fascination with the futuristic has also intrigued myself ever since I was very young, and in our home town of Kaiapoi, my brother Barry and I would watch the Anglo American TV Series UFO, and at the time we had a collection of books Mum bought which showed stuff like the War of the Worlds, so Science and Science Fiction has always held my interest.
The title " Walk the Line " is a paraphrasing of I Walk the Line, a song by Johnny Cash, in this instance, as well as Walk the Line being a 2005 American biographical drama film directed by James Mangold. ( From Wikipedia ). It also has other meanings.
As to the title " The Odd Couple ", this can be seen as a reference to The Odd Couple, a 1965 stage play by Neil Simon, The Odd Couple (film), a 1968 film based on the play, and The Odd Couple (TV series), a 1970–1975 television show based on the film, which I watched as a kid.
Any quote or part of this material which seems to belong to any other author should be treated as such, and I claim no ownership of anything I did not myself invent or discover, nor of any obvious copyright, trade mark, or registered trade mark.
The Adventure continues in the next Hubs on Right Angled Triangles, Trigonometry to begin with and Pythagorean Theorem and Triplets.
Also if You are curious, please check out the other Hubs, The Maths They Never Taught Us - Part One, The Maths They Never Taught Us - Part Two , The Maths They Never Taught Us - Part Three, The Very Next Step - Squares and the Power of Two , And then there were Three - a Study on Cubes, Moving on to Higher Powers - a First look at Exponents, The Power of Many More - more on the Use of Exponents, Mathematics - the Science of Patterns , More on the Patterns of Maths , Mathematics of Cricket , Things to do with Shapes, Pyramids - How to find their Height and Volume, How to find the Area of Regular Polygons, The Wonder and Amusement of Triangles - Part One, The Wonder and Amusement of Triangles - Part Two, the Law of Missing Lengths, The Wonder and Amusement of Triangles – Part Three : the Sine Rule, and The Wonder and Amusement of Triangles - Part Four : the Cosine Rule.
Also, feel free to check out my non Maths Hubs :
Bartholomew Webb , They Came and The Great New Zealand Flag
Just take a good look at it, and note how interesting it all is, then see if you can come up with anything else along the same lines. As usual, I would appreciate any comments, feedback and suggestions which would be given due credit, or indeed have a go and publishing Your ideas Yourselves, but firstly, by all means, add Your comments - it's a free Country.