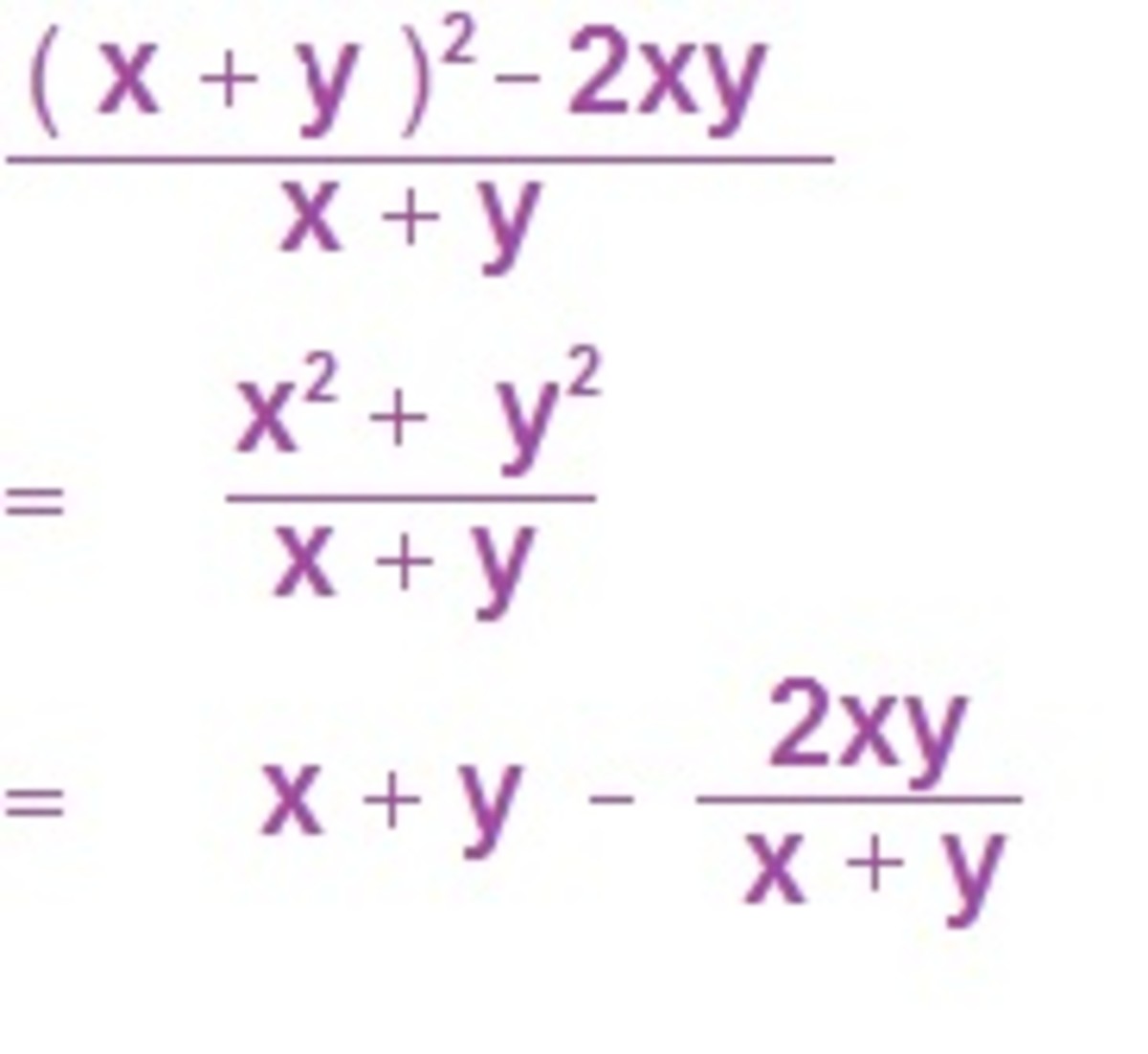Things to Do With Shapes
Without Form it is Void
Moving on from the topics covered in both Trigonometry to begin with and PythagoreanTheorem and Triplets, which we shall see a lot more of soon enough, let’s look at an aspect of geometry which also has some facts of interest.
If you take a triangle, and draw a line between what we call the midpoints of two of its sides, this line is exactly parallel to the third side. Incidentally, the midpoint of a line is pretty much what it suggests - the point on the line in the very middle between both ends of it. Let’s see :

About these Midpoints
In fact you don’t even need to use the midpoints - as long as the line coming off one side of the triangle does so at the same angle as the side you are trying to be parallel with, then it will work. But if you do use both midpoints, the interesting thing is, that the smaller triangle you form has exactly one quarter of the area of your original triangle.
Actually, this makes sense, since it relates before to what we were talking about with areas going fourfold when both sides are doubled, and in effect what you are doing with the triangle by forming a second smaller one from the larger one’s midpoints, is to halve the sides of the smaller triangle, and therefore quarter the area. The same thing can also be done to a square, if you join up two lines from the midpoints of two of its sides :

About the Picture
We see above that the smaller square formed from joining together two lines at a right angle from the midpoints of two of the larger square’s sides will have an area one fourth that of the larger square.
Triangles Return
But getting back to triangles, as suggested, if we do halve the lengths of its sides, we quarter its area. The only difference is the number of sides we are reducing in length, which itself will affect the perimeter of the shape we are dealing with.
This is another interesting aspect to do with shapes - the idea of Area vs. Perimeter, since both can be related, but not in a completely direct way. So let us look at this idea of area vs. perimeter right now.
Getting Round to it
If I were to ask you what shape gives us the most area for the length of its perimeter, what would you answer ? To find the correct answer, by all means , have a look at the illustration below :

Points to Ponder
Think of it this way. At the other end of the scale is the triangle ( Δ ), and if you imagine one corner of a triangle, where two sides meet, being able to come apart, as if the other two corners were hinged, you could see it open up. A gap would then form between the two separated ends, as if you could place a fourth edge between them :

Musings on the Diagram above
But in this case, all the sides of the square would equal each of those of the triangle, so with four sides being the same length instead of three, naturally the perimeter would be larger. But what I am trying to show here is that the perimeter of the square actually needs only to equal that of the triangle, and yet even so, its area would still be a bit larger.
What is needed, and is recommended in any case is for us to see for ourselves that the best shape for area is the circle, then it goes down the many sided multilongnameagons, to the hexagon, pentagon, square and then triangle, this last one giving us the least amount of area for the size of its perimeter.
The relationship between circles and polygons with ever increasing numbers of sides was used by the Ancients of China, the Arab lands and Greece to work out the value of pi, as a circle could almost be seen as a polygon with an infinite number of very small sides, but there is more to it than this. Certainly though, as the number of sides of a polygon increases, but the perimeter remains the same, such polygons can hold greater area than those with less sides, and it is as if the circle is the limit of such achievement - analogous to limits used in Calculus and other disciplines.
Perimeters of Shapes - the Circle
Okay, so let us imagine every single one of our shapes has a perimeter of twelve inches. All we need do from this is deduce its area.
Circle : Formula for the area of the circle is : π r², but to find the area we first need to work out the circle’s radius, and seeing we already know its perimeter, or rather, for a circle specifically, its circumference, this shall not be too hard to work out. The formula for the circumference is 2 π r, and in this case 12 = 2 π r, so what we do is see that this means that 12 ÷ 2 = π r, which means that π r = 6, and therefore that 6 ÷ π = r. From my trusty calculator, I see that 6 ÷ π = 1.91 ( rounded up to two decimal places ), so it is this value that we put into the formula for the area of a circle, which again is π r². The answer we get when we do this is 11.46 square inches ( rounded up to 2 d.p. )
We could also realise that because the area and circumference formulae for the circle both involve pi, we can find a relationship between the two, by looking at π r² ÷ 2 π r = r ÷ 2, so the area divided by the circumference is equal to half the radius, which may help in some situations.
Perimeters of Shapes - the Square
If we then consider a square with a perimeter of also twelve inches, we realise, that because it has four equal sides, (squares tend to do that, you know), well, twelve divided by four equals three, so our area for this particular square is three times three, which equals nine square inches - a bit less than the 11.46 we got for the circle, even though both are bounded by exactly the same length.
Perimeters of Shapes - the Triangle
Looking then at the triangle, it has to have three equal sides of four inches ( I’m dealing with regular polygons here - triangles, hexagons, pentagons, will all have sides of equal lengths - the only exceptions will be rectangles - suffice to say, I am not going to have a triangle with three sides of different lengths ).
Now the formula for the area of the triangle is ½ base × height. In this case, half the base is equal to two inches, but to find the height, we have to use a little trigonometry. Now you see why I went over it before. Remember always, you are the student, and I am the master. And in trying to work things out, so that you don’t make a mistake, take your time, and don’t try to go at anything over 60 perimeters an hour.
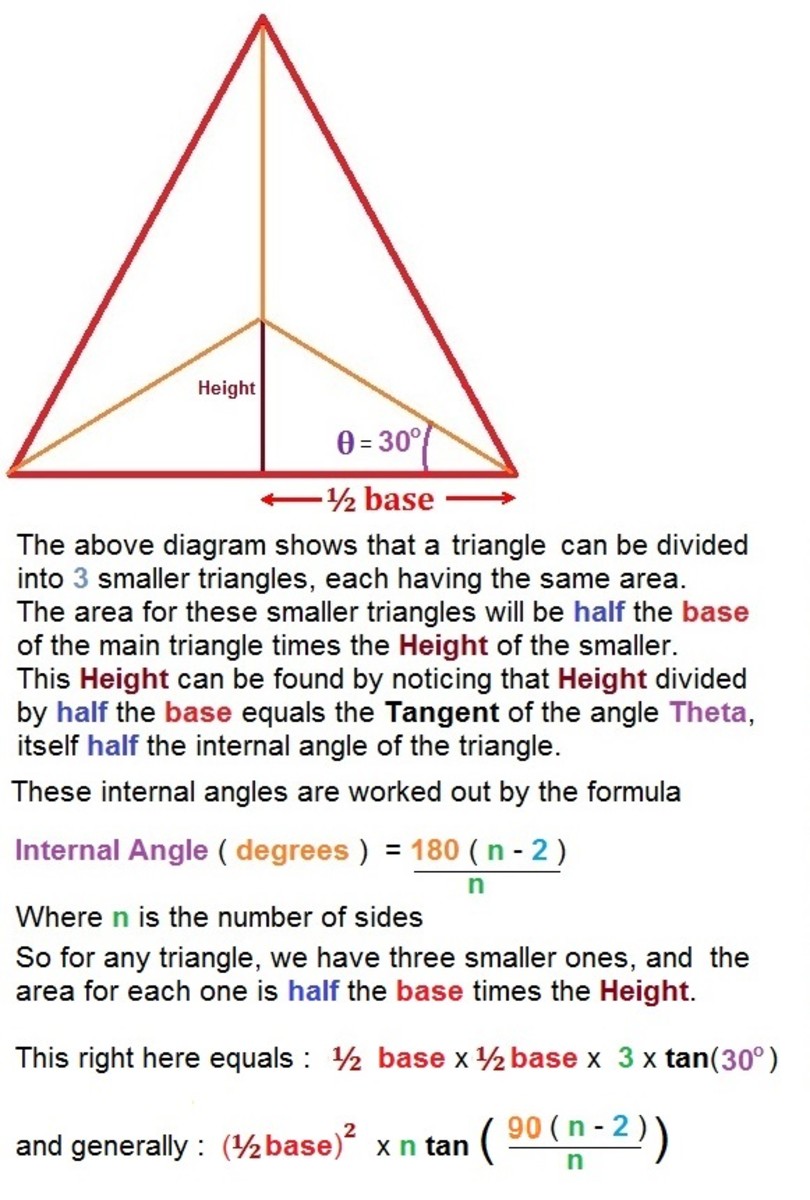
What we do is imagine a centre line from the very top point of the triangle, cutting it down the middle in two to the midpoint of the base, forming two equal sized right angled triangles with sides equal to four inches, two inches, and the height that we don’t know. The height is this perpendicular, vertical line bisecting the main triangle. To clarify this, I shall illustrate :

What we can gather
The triangle in question is equilateral, therefore its internal angles are each of sixty degrees. This is the size of the angle θ at the bottom corner. All we do, knowing that the tangent of an angle is its opposite over its adjacent sides, and that half the base is the adjacent, and the height is our opposite, is we work out the height to be equal to 2 tan 60, which is 3.464, and when we multiply this height by half the base, which is two, we get 6.93 square inches - once again even less area than that encompassed by the magnificent circle.
Of course, knowing both hypotenuse and adjacent, we could also use Pythagoras to find the height, by subtracting 2² from 4², to give ourselves twelve, and finding the square root of this, which is also 3.464. Let’s look at a rectangle with perimeter twelve, to see how much area it can hold.
Towards finding a Pattern
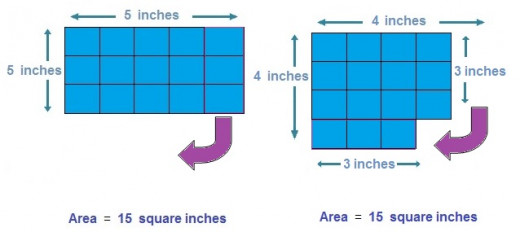
We’ll say then that our rectangle has dimensions of 2 × 4 inches. This gives it a perimeter of 12, since it has two sides of two inches ( = 4 ), and two more of four inches ( = 8 ), but its area ends up being only eight square inches, slightly less than the nine square inches encompassed by the bounds of the square.
Now, if we alter the dimensions of the rectangle slightly, to give it two sides each an inch long, and the other two are each five inches long, we get an area of only five square inches, even less than that of the previous rectangle. Generally speaking, we can gather from this that, the narrower the rectangle, the less area it can encompass for the length of its perimeter, and in fact these differences in area actually form a pattern, the table for which is below :
Area vs. Perimeter
10 x 10
| Square
| = 100 square inches
| difference = 0²
|
11 x 9
| Rectangle
| = 99 square inches
| difference = 1²
|
12 x 8
| Rectangle
| = 96 square inches
| difference = 2²
|
13 x 7
| Rectangle
| = 91 square inches
| difference = 3²
|
14 x 6
| Rectangle
| = 84 square inches
| difference = 4²
|
15 x 5
| Rectangle
| = 75 square inches
| difference = 5²
|
16 x 4
| Rectangle
| = 64 square inches
| difference = 6²
|
17 x 3
| Rectangle
| = 51 square inches
| difference = 7²
|
18 x 2
| Rectangle
| = 36 square inches
| difference = 8²
|
19 x 1
| Rectangle
| = 19 square inches
| difference = 9²
|
Other Means to work this Problem
In the advanced subject of Calculus, there are techniques available to work out the greatest possible area for a shape of given perimeter or dimensions. This is of course far beyond the scope of this book, but for us to understand why there is a difference in the area bounded by rectangles of the same perimeter just because some are thinner, let’s first look at it mathematically, to see if we understand.
By Maths
Imagine you go from the square, being 10 × 10, to a rectangle that is 15 × 5. One has an area of 100 square inches, to one measuring only 75. Look at each dimension. Sure, the 15 is 1½ × 10, but its co dimension of 5 is only half that of the other ten, so while we are multiplying by 1.5 on the one hand, we end up dividing by 2 on the other. In effect we are multiplying by ( 1.5 ÷ 2 ), which equals .75, and indeed 75 is .75 of 100.
What happens when you lengthen one side but shorten the other to make the rectangle narrower, is at first you would add area, but then you would take more away. As an example, if you were to go from the square ( 10 × 10 ), to the first rectangle ( 11 × 9 ), imagine first that you go to 11 × 10, so initially you have added ten square inches. But then, when you go from 11 × 10 to only 11 × 9, you have one less 11 than before, so you lose 11 square inches - a total loss of one square inch.
And it must have some kind of significance, that the losses of area each time we thin out our rectangle, occur as the square of a number, and the number in question happens to be the difference each dimension of the rectangle has to the sides of the original square. For example, with respect to the rectangle 5 × 15, 5 is five less than ten, while 15 is five more, so the overall difference in area ends up being 5². This of course, applies when you begin with a square measuring 10 × 10, but had we started with a 6 × 6, our next rectangle will be 5 × 7, which is only one square inch less in area, because this time 5, like 7, would only be one away in value from six.
Using Algebra
Algebraically we have : ( x - 5 )( x + 5 ) = x² - 25, where x = 10. This set up is vaguely familiar, and is known as the sum and difference of two squares, which we have seen before in our studies on multiplication. In fact, all this work on areas and perimeters of quadrilaterals is basically the practical side to such algebraic identities. This proves that mathematics does have actual use in the real world, but did you know that around the turn of the Twentieth Century was a brilliant English mathematician by the name of Hardy, ( a companion of both John Littlewood and the exceptional Indian number theorist Ramanujan – whose picture is in my Hub Mathematics of Cricket ). Professor Hardy, who wrote classic books on maths, did not believe mathematics ought to be used for anything practical, but admired simply for its own sake. Maybe a bit of both.
A Demonstration
I thought it good to demonstrate what happens for real when you go from a square shape, and progress down the different rectangles, all of the same perimeter. As you might have noticed, the beauty of shapes of the same perimeter, is that you don’t have to do much working out to find the dimensions of the next shape. In every case, all you do is add one to one dimension, and subtract one from the other - in effect leaving the perimeter the same, but altering what the area will be.
Same perimeter, different area
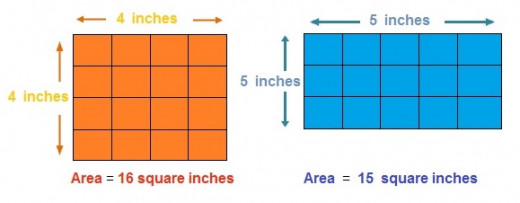
From the above diagram to the one below
With reference to the diagram of the two shapes above, if we were to take the three squares going down the right hand edge of the rectangle, and place them along its base, we would have the shape of the square to the left, minus one smaller square, yet both shapes have the same perimeter of sixteen. What the action of ‘thinning’ the square does, as touched on before, is to take away a row ( in this case the bottom one ), which holds four small squares, and replace it with a column only able to hold three, so it stands to reason that some area is lost.
The same process is then repeated as the rectangle is allowed to become even narrower - all the time holding the same perimeter, but allowing this boundary to close in, as it were. Imagine, if you will, a string formed in the shape of a circle, then one gets hold of both sides of it, and pulls outwards. The circle will thin to become like an ellipse, then even more so, until it resembles two lines almost side by side - joined together as one, but with no area in between them, yet the circumference has in no way changed - we did not cut any of the string away - all we did was pull. This in effect is what happens to the square which becomes an ever narrowing rectangle.
I have in my possession a table, which I shall not as yet print, except by popular demand, of all the possible perimeters of four sided figures, where each side has to be a whole number. If you consider you will realise that all of these perimeters have to be even, and as we go down the list from 1 × 1, all the way to 6 × 6, the number of possible dimensions increases, and there is a noticeable pattern to the relationships within the table.
On the page opposite the table, I write about the idea of a possible formula for guessing the exact dimensions of the quadrilateral, given its area and perimeter. But the technique for solving such a thing exists in Calculus, and rather than a formula there is a process. For example :
Let us say we have a four sided figure with an area of 88 square inches, and a perimeter measuring 52 inches, if it is not a square, what are its dimensions?
We name our dimensions as x and y. Here we have the fact that x + y = 26, and xy = 96. What do we do ?
We want the area in terms of one variable only, so we say that y = 26 - x, and state then that x( 26 - x ) = 96.
Let me continue . . .
From this we can say that 26x - x² = 96, and also that this means that 26x - x² - 96 = 0, or better yet, that x² - 26x + 96 = 0.
Factorise : ( x - 22)( x - 4 ) = 0.
This tells us our dimensions are 22 × 4, which do indeed multiply to give us 88, and adding the two gives us 26, which we then of course multiply by two to give us the total perimeter of 52.
This is solved by working out what two numbers add to make -22, and multiply to give 88, or you could use the Quadratic Formula, if it won’t go evenly, and you end up with non whole numbers.
So as we have seen, a given perimeter can encompass any number of different areas, and by the same token, the one area can have different size perimeters. But if you state a given area has to have a certain perimeter, then the dimensions for that particular shape are unique. Given an area and a perimeter, you can, as I have said, use Calculus to work out the dimensions. First of all, whatever your shape is, you name each dimension by assigning them the letters x and y, respectively. Then you realise, that all a perimeter is, is 2x + 2y, and that the area is x × y. Let’s do another area vs. perimeter calculation, to check it out again.
Well, look, say we have a quadrilateral whose perimeter is 18 inches, and its area measures twenty square inches. This tells us that 2x + 2y, or, 2(x + y) = 18. This means that x + y = 9, but we have to express y in terms of x, by saying that y = 9 - x, as we did before in the other example, so that when we give our area, we will be able to express it simply in terms of x, and not have to worry about y. Y not ?
Area = xy, or x(9 - x), which, when we expand and simplify, we find to equal 9x - x². Now, if we were to differentiate this, then set the derivative to equal zero, we would be able to find the value of x that gives us the maximum area for a quadrilateral with this perimeter : dy / dx (9x - x²) = 9 - 2x = 0 x = 4.5
Which is true, since this would end up being a square with all four sides 4.5" long, but then our area would end up being 4.5², which is 20.25 square inches, but what we want are dimensions for one with an area of only twenty. This then would be one where 9x - x² = 20, and therefore where we can say that 9x - x² - 20 = 0. If we use the Quadratic Formula for this one, we can find that our two values equal 5 and 4.
The last thing I would like to show on this particular subject is a formula I came up with to calculate the areas of regular polygons, by which I mean, ones whose sides are all of the same length.
( ½b )² × tan ½( θ ) × n
b = base ( or length of each side )
θ = interior angle within polygon, all are the same
n = number of sides the polygon has
So, for instance, if you wished to find the area of a square, whose sides are all three inches, well of course the answer is nine square inches, but let’s try it out, in order to ascertain its reliability.
b = 3 n = 4 θ = 90° ( there are four internal angles in a square, adding up to 360°. The formula for working out the total number of degrees for all of a regular polygon’s internal angles, is that you take the number of its sides, subtract two, then multiply by 180. Then to find what each angle equals, divide this number by the number of internal angles the shape has, which is also the same as the number of sides it has. )
Now what this whole formula of mine tells us, is to multiply the square of half the base by the tangent of half the internal angle, and then by the number of sides, so :
( 1.5 )² × tan 45° × 4 = 9, since tan 45° = 1
Remember, curls and toys, to keep the ½ within the parentheses, and multiply the base before you square it. It is ( ½b )², NOT ½b², and then remember also to find the size of one internal angle, ( not all of them ), then halve it, before finding its tangent. Just to make things clear, let’s do some more, and see if it only works with regular polygons.
Let’s see if we can use it to find the area of the 3 : 4 : 5 right angled triangle, the base triplet.
Again, this is a simple one you don’t really need the formula for, and I really developed the formula so I could work out the areas of pentagons, hexagons and ones like that. However, I shall use this example so you can see what actually happens.
In this triangle, b = 4, and h = 3, so that the area is in fact six square inches, so let’s see what the formula comes up with.
(½ × 4)² × tan 30° × 3 = 12 × .57735 = 6.9282
So obviously it doesn’t work here, because the sides are all of different lengths. The key to solving the area of a right angled triangle, is to do as I have done here, which is to make sure the right angle is at one of the bottom corners. Your hypotenuse does not figure in the calculations, but rather your other two sides - known as the legs of the triangle - are simply multiplied together, and then this value is halved, and so you have your area.
Otherwise for any triangle you can use Heron’s Formula, which is :
√[p(p - a)(p - b)(p - c)]
Where p is the semi - perimeter, and a, b and c are each of the three bases. The semi - perimeter is half the value of all three sides added together, so all we for this one, is subtract each base in turn from half the perimeter, then multiply all three of these values by half the perimeter, then find its square root. For example :
3 : 4 : 5 triangle perimeter = 12 ÷ 2 = 6 = p
So we get : √[ 6(6 - 5)(6 - 4 )(6 - 3)] = 6
So this formula works for that kind of triangle.
But does my formula work for an equilateral, as I have claimed it does ? Let’s see.
Base = 5", meaning all three sides equal the same.
( ½× 5)² × tan 30° × 3 = 10.8253
The way to see whether this is true, is to work out the area of such a triangle using the method I employed previously when I cut the equilateral I had through the middle. All you do is multiply half the base of the triangle by tan 60°, to find the height of the thing, and then multiply this height by this half of the base : 2.5 tan 60° = 4.33 × 2.5 = 10.8253
So, it does work ! But again, there are other reasonable techniques for the purpose of finding areas of polygons with sides four or less. But try finding that of a pentagon in a hurry, and you’ll see why I worked this baby out. The only drawback of course, is that for the formula to work, all the sides do have to be of the same length.
So there are many ways and means within mathematics to work out any old problem, however hard it may seem at the start.
Disclaimer
As much as some of this Hub contains certain Mathematical knowledge accessible in the public domain, and not subject to any Copyright, other information has been drawn from textbooks which themselves are Copyright, but only in the sense of how they deliver the information which itself is shared and sometimes ancient Mathematical knowledge. Other information has also been found on Wikipedia ( Copyright 2013, the Wikimedia Foundation ), which is a good source of information. Part of this is also my own discovery, but may also independently have been found by others.
Some of the illustrations in this particular Hub are my own, and have primarily been done using Microsoft™ Paintbox, edited from illustrations done using Microsoft™ Word. Any others, if they are here, are, as noted, from Wikipedia. Any quote or part of this material which seems to belong to any other author should be treated as such, and I claim no ownership of anything I did not myself invent or discover, nor of any obvious copyright, trade mark, or registered trade mark.
The Adventure continues in the next Hubs on Geometry, and these are : Pyramids - How to find their Height and Volume, as well as How to find the Area of Regular Polygons,
If You are curious, then do not hesitate to take a good look at the other Hubs, The Maths They Never Taught Us - Part One, The Maths They Never Taught Us - Part Two , The Maths They Never Taught Us - Part Three, The Very Next Step - Squares and the Power of Two , And then there were Three - a Study on Cubes, Moving on to Higher Powers - a First look at Exponents, The Power of Many More - more on the Use of Exponents, Mathematics - the Science of Patterns , More on the Patterns of Maths , Mathematics of Cricket , The Shape of Things to Come , Trigonometry to begin with , Pythagorean Theorem and Triplets, The Wonder and Amusement of Triangles - Part One, The Wonder and Amusement of Triangles - Part Two, the Law of Missing Lengths, The Wonder and Amusement of Triangles – Part Three : the Sine Rule, and The Wonder and Amusement of Triangles - Part Four : the Cosine Rule.
Also, feel free to check out my non Maths Hubs :
Bartholomew Webb , They Came and The Great New Zealand Flag
There will also be many More to come on a wide variety of Subjects.
Just take a good look at it, and note how interesting it all is, then see if you can come up with anything else along the same lines. As usual, I would appreciate any comments, feedback and suggestions which would be given due credit, or indeed have a go and publishing Your ideas Yourselves, but firstly, by all means, add Your comments - it's a free Country.