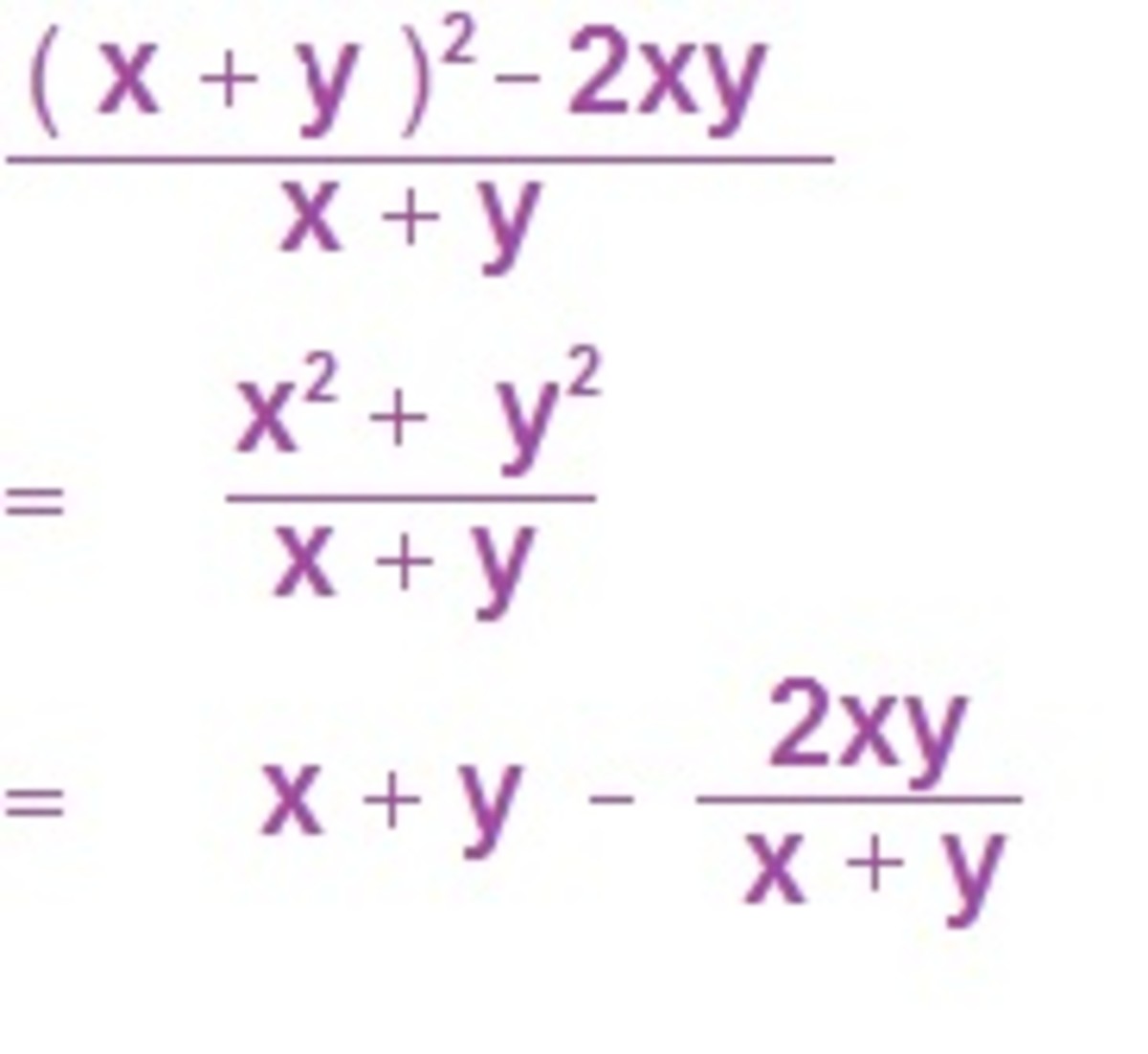The Maths They Never Taught Us - Part Three
It does work both ways
Let's Mix Politics and Sport
Now the next idea I would like to draw your attention to, as touched upon in the previous section on opposite operations, back in The Maths They Never Taught Us - Part Two , is that if numbers work out one way, then they should work out another.
So, just as the order of the terms in some operations do not matter, then there is more than one way to solve a mathematical problem, and by doing it more than one way, we can even confirm that our first answer was correct.
To illustrate this, let us check out a recent historical Netball Test between the Australian Diamonds and the New Zealand Silver Ferns.
Australia vs. Silver Ferns, World Netball Championship Final, Liverpool Arena, Sunday, 21st July, 2019
1st Quarter 2nd Quarter 3rd Quarter 4th Quarter Aust 10 Aust 15 Aust 12 Aust 14 NZ 10 NZ 18 NZ 13 NZ 11
FINAL SCORE : Australia 51 New Zealand 52
For this genuine, historical test, another way to check the margin of victory, as opposed to looking just at the final score, is to add all the quarters together, and compare them. So, let us take it one quarter at a time
Brisbane Test Analysis by Quarter
1st : Even 2nd : NZ + 3 3rd : NZ + 1 4th : Aust + 3
If we look at it from Australia’s point of view, quarter by quarter, we see that after the 1st, the Diamonds were even with the Silver Ferns. In the 2nd Quarter, New Zealand came back to win it by three, meaning that at Half Time, Australia was now down by three. In the third quarter, New Zealand extended their lead by one more, being thus now up by four. Thusfore, Australia was now down by four, but in the final Quarter, the Australians scored three nets more, leaving them a total of one point short, as the final score confirms. One could also look at it in that the respective quarters in which each team scored three more than their opponents cancel each other, that is, the second and fourth quarters negate each other, the first quarter, the even one, does not have an affect, so in affect New Zealand won by what they did in the third quarter. Now, this leads us to another interesting mathematical idea, which has relevance to a number of things, from sport to politics.
Golden Oldies Division Tournament, Australian Open Final, Centre Court, Rod Laver Arena, Flinders Park, Melbourne, January, 2056
Roger Federer ( SUI ) 6 0 5 7 10 Rafael Nadal ( ESP ) 4 6 7 6 8
We see here that once again the Swiss Maestro has triumphed in a mammoth five setter, by three sets to two, but if we look at the total number of games won by each player, we can determine that although he lost the match, the Spaniard actually won 31 games to Federer’s 28, which works out if you also calculate it set by set. This is the nature of tennis. It is not won by games, but by sets, and each set is treated individually.
And yet if we were to investigate the details of this contest further, even though it is not evident on our scorecard, we would find that in this particular match at least, most of the time Mr. Federer won a game, he did so by going to forty love, then winning the next point, while Mr. Nadal was more likely to win by taking the game to deuce, then getting the next two points in a row. It works out then, that although Nadal did win more games, Federer actually won more points. And this kind of thing doesn’t only occur in Tennis.
Was our HART really in it ?
In 1981, the South African Rugby Union team, the Springboks, toured New Zealand, amid huge protest. Sporting contact with such a country always caused considerable controversy, due to the policy of Apartheid then practiced by South Africa. In 1981 people witnessed the greatest civil unrest seen here in New Zealand since the Watersiders' Strike of 1951, as those opposed to The Tour went out to do battle with Police riot squads outside each game’s venue, in an effort to stop each match.
Now with all this happening, the All Blacks won the First Test at an unjaded Lancaster Park, here in Christchurch, by 14 - 9. After this, they lost the Second Test at Athletic Park in Wellington by 24 - 12. The Third Test went to Eden Park in Auckland, to give the All Blacks a victory by 25 - 22, and a hard earned and rare at the time test series win over South Africa, beating the Springboks by two tests to one.
Yet again, though, we see that if we add up all the points scored by both teams in the test series, New Zealand in three tests scored 51 points to South Africa’s 55. This gave South Africa four more points overall. You can calculate this margin either by adding the teams' points for each match together, then comparing, or even adding the margins of victory for each match, and working it out from there.
Now, the fact that South Africa did score more points in all three tests combined, is actually of no real relevance, since each test is played separately from any of the others, and it is what happens on the day that decides defeat or victory. But this analysis of the previous serves to prove the point that you can work out totals of any kind of thing in more than one way, and if both answers don’t match, then you know that you have a bit of a problem. It is best to get into the practice of doing things this way for verification, even if it seems like double handling. Doing calculations in more than one way is in fact a common practice for scientists and mathematicians to enable them to check their answers.
Actually, recalling recent ( November 2013 ) events, there are times that points in an individual game do count, and that is in World Cup Soccer qualifying. Two countries will be paired up to play off against each other, in these cases at least, the aggregate number of goals count, especially away goals. There is a lot of relevance for mathematics in looking at how this works, which may be done at a future time.
Last past any Post
Now, this idea of separate games counting, as opposed to total overall points in a series, may be the same sort of story in the way some Elections are carried out. Historically, up to and including 1993, General Elections in New Zealand were carried out using a method known as First Past the Post. Since 1996, New Zealand changed to employ a form of Proportional Representation known as MMP.
In the old days there were a certain number of Electorates, which only changed as the population increased, and some seats were added, and boundaries redrawn. These Electorates were geographical areas determined so that each contained about the same number of voters. In every Electorate, which represented a Seat in Parliament, a number of candidates would stand to be chosen as that Electorate's Member of Parliament. This meant that each voter, wherever they were in the country, would be choosing a local candidate, rather than all the votes throughout New Zealand being pooled together, added up, and the party that got the most votes winning.
This was where First Past the Post resembles the set by set play of tennis, as well as the on the day rugby score, regardless of total games won in a tennis match, or points scored in a test series. In fact, on at least two occasions, in 1978 and 1981, the ruling National Party under Robert Muldoon won with less votes than their major rival, the New Zealand Labour Party, lead then by Bill Rowling. How could this in principle outrage occur ? Well, remember the tennis match, as I have just said ? Basically, a First Past The Post Election can be simplified to resemble one such match :
Simplified Example of First Past the Post Election for the Simple
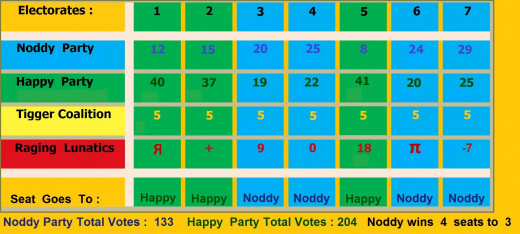
Analysis of First Past the Post
Now we can see that even though the Happy Party was given a total of 71 Votes more than the Noddy Party, the Happy Party loses the election by four seats to three. This kind of thing is also why the loser of the 2000 United States Presidential Election, Mr. Al Gore, could get more votes than the winner, who went on to become two term President George Bush, Jr., so that although America narrowly missed being gored, they may by now be well and truly bushed. This is known in Florida as the Butterfly Effect. This is because, even though Americans do not employ a first past the post system exactly like New Zealand once had, their electoral system is still engineered so that votes are not used effectively in a similar way.
We can see from the table that the reason for these kinds of occurrences, is that when the winner of the election wins a seat, they do so by a narrow margin, and yet when they lose one, they get well and truly beaten, so that all the extra votes the losing party gets in a given electorate are sort of wasted.
We look now at another clever aspect of Mathematics, which forms the basis of how we figure out equations in many different forms, and how we can go from expressing a truth in a certain way, to ways in which the same thing can be put from a different point of view
For every Action there is an equal and opposite Reaction - not just in Physics
Having been looking at how things can work out in more than one way, we come now to the subject of Opposite Operations. Look at this equation : 16 × 9 = 12 × ?
So how do we work out the mystery number which will make the equation true ? Let us imagine we changed the 16 on the left into the 12 on the right. To balance out the equation, we would then have to change the 9 on the left into another number which corresponds to it, just as 16 here corresponds to 12.
Now, in order to know what to change the 9 into, we need to find out what we have done to the 16 to turn it into the 12, and then we go and do the opposite thing to the 9, which will balance out both sides of the equation.
What is 16 to 12 ? Well, in order to turn 16 into 12, we actually had to multiply by ¾.
That is : 16 × ¾ = 12, or 12 is ¾ of 16.
But what do we do to 9 ? The opposite - we divide it by ¾. 9 ÷ ¾ = 12
And so we end up with : 16 × 9 = 12 × 12 = 144
An even simpler example may also help to explain : 3 × 2 = 6 ; 6 × 1 = 6.
This time, in the equation at left we doubled 3 to get 6. If we want to instead use 6 in place of 3 on the left hand side of the multiplication symbol, then in order to balance the equation, we have to halve the 2 that is there to get 1. So we could say :
3 × 2 = 6 ; ( 3 × 2 ) × ( 2 ÷ 2 ) also = 6.
Because in the second part above, the 2’s cancel out.
In more general form : ( a × b ) × ( c ÷ b ) = a × c
Since, as we can see :
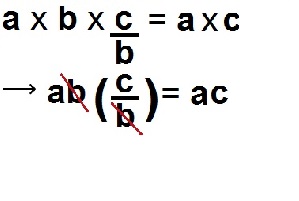
There's a Fraction too much Fraction
Speaking of fractions, because there are some interesting ways in which these entities behave, they do tend to catch people unawares, so when confronted with them, we need to be very careful.
20 ÷ 10 = 2 ÷ 1 = 2, and so ( 20 ÷ 10 ) ÷ 2 = 1, but 20 ÷ (10 ÷ 2) = 20 ÷ 5 = 4.
We got a larger answer the second time, because we divided our denominator, the number we were originally dividing by, by two, which means we ended up the second time dividing by a lesser amount, and when we do that, our answer ends up greater.
For example : 20 ÷ 20 = 1 ; 20 ÷ 10 = 2 ; 20 ÷ 5 = 4 In the cases you have just seen, as the denominator (the value on the bottom of the fraction), decreases, the value of the fraction as a number increases. Correspondingly, though, if we decrease the value of the numerator, (the top part of the fraction), then the value of the fraction also decreases.
Incidentally, decreasing the value of the denominator has the same effect as increasing that of the numerator, and vice versa, so that if I, instead of dividing the denominator by two as I did before, multiplied the numerator by two : ( 20 × 2 ) ÷ 10 = 40 ÷ 10 = 4, which is the same answer I had before.
You need to be very much aware of what you can get away with when using fractions, so it is always best, when playing around with them, to check out your answers once you’ve finished.
For example : 20 ÷ ( 10 ÷ 2 ) is not the same as 20 ÷ 10 ÷ 2, which equals 1. This is because the parentheses in the first equation allow 10 ÷ 2 to be considered as one number. This is from the principles of BODMAS, which I shall go into more detail about later. Suffice to say, that the numbers in the parentheses ( ) are worked out first, but where there are no parentheses, as in our 2nd example : 20 ÷ 10 ÷ 2, we end up dividing twice, first we divide 20 by 10, and then divide the answer to this by 2.
In effect, actually, what we have above without the parentheses is the same as saying 20 ÷ ( 10 × 2 ), or 20 ÷ 20, which itself is not to be confused with the expression 20 ÷ 10 × 2, which, without the parentheses, ends up equalling 4.
Now, you may also be aware how to multiply and divide fractions. We see that if are to multiply two fractions, we times the top numbers ( numerators ) together, and then the bottom ones, ( denominators ), together, as well.
For instance : ( 3 ÷ 5 ) × ( 4 ÷ 7 ) = ( 3 × 4 ) ÷ ( 5 × 7 ) = 12 ÷ 35,
But if we wanted to divide ( 3 ÷ 5 ) ÷ ( 4 ÷ 7 ), we flip the second fraction, then multiply :
( 3 ÷ 5 ) ÷ ( 4 ÷ 7 ) = ( 3 ÷ 5 ) × ( 7 ÷ 4 ) = ( 3 × 7 ) ÷ ( 5 × 4 ) = ( 21 ÷ 20 )
Now the reason you flip the second fraction is because that is the one being divided by the other. If you went and did it the other way, and inverted the first fraction, you would then end up with the answer ( 20 ÷ 21 ), which is not really the same.
Do unto Others ? Let us Reciprocate
As a matter of fact, this second number is the reciprocal of the first. We obtain the reciprocal of any number by dividing 1 by it, ( thus, ½ is the reciprocal of 2, since it is the same as saying one divided by two ). We can also find the reciprocal if it is a fraction, by inverting it, such that ( 4 ÷ 3 ) is the reciprocal of the fraction ( 3 ÷ 4 ), and is quite simply also the same as saying 1 ÷ ( 3 ÷ 4 ). Another thing to be aware of with these fractions, is that, for example, ( 3 ÷ 5 ÷ 4 ) ÷ 7 = ( 3 ÷ 5 ) ÷ ( 4 ÷ 7 ), but not 3 ÷ 5 ÷ 4 ÷ 7. 3 ÷ 5 ÷ 4 ÷ 7, though, does equal ( 3 ÷ 5 ) ÷ ( 4 × 7 ), which also equals 3 ÷( 5 × 4 × 7 ).
Along with this, there are a number of other facts with fractions which are very useful to know :
If a ÷ b = x ÷ y ( a is to b what x is to y ) ay = xb
Example : 3 ÷ 6 = 12 ÷ 24, so that 3 × 24 = 6 × 12
Because : if, as we said, a ÷ b = x ÷ y, this also means that a = b × ( x ÷ y ), which equals bx ÷ y, so that since bx ÷ y = a, then we see that bx does equal ay. All this is simple manipulation of formulae by changing the subject. As long as we know what we’re doing.
Not so dirty Double Cross
So, what if you want to add fractions with different denominators ? Sure, you could cross multiply, where you multiply the numerator of each fraction by the denominator of the other, then multiply both denominators together, but there is another way.
I have come up with what I call the Fractional Difference Formula, which allows us to add or subtract fractions with different denominators and numerators.
Imagine you have a two fractions, ( y ÷ x ), and the other, ( y + b ) ÷ ( x + a ), where y + b represents whatever y is equal to at the time, plus the value of b to make a new number, and the same with x and a.
Say, for example, we wanted to add ¾ to ⅔. If we say that three quarters is represented by the symbols ( y ÷ x ), then two thirds would be equal to ( y + b ) ÷ ( x + a ), where 2 is y + b, and 3 is x + a.
In this case, since we decided that ¾ = ( y ÷ x ), then y = 3, and x = 4, so to make y + b equal to 2, b must = - 1, and then for x + a to be equal to 3, a also equals - 1, ( but not necessarily always so. ) It is also true then that a, b, x and y can be either positive or negative.
Now our formula to add these two is :
( y ÷ x ) + [ ( y + b ) ÷ ( x + a ) ] = { [ x( 2y + b ) ] + ay } ÷ ( x² + ax )
{ [ 4×( 6 + -1 ) ] + -3 } ÷ ( 16 + -4 ) = 17 ÷ 12, which is indeed correct.
( Here we see x², which, as I mentioned before, is just a shorthand way of saying x times x. )
Another formula exists if we wish to subtract any fractions, so let’s try ¾ - ⅔. The equation for this is : ( y ÷ x ) - [ ( y + b ) ÷ ( x + a ) ], = ( ay - xb ) ÷ ( x² + ax )
and so my formula for working this out will be :
( ay - xb ) ÷ ( x² + ax ) = ( -3 - - 4 ) ÷ ( 16 + -4 ) = ( 1 ÷ 12 ), which is also certainly the correct answer.
By the Formula
Now, whether or not you find cross multiplying easier, this is still the kind of formula that can be very useful, especially if you have one of those programmable scientific calculators which allows you to plug formulae in, and can automatically give you an answer once you give it the value of each variable. These two equations were developed over a period of time as I experimented with various formulae before realising that I could whittle them down to two basic ones to handle all eventualities. The formulae themselves can be shown to work by applying some basic algebra, using the same method one would need to employ to cross multiply the normal way :
( y ÷ x ) + [ ( y + b ) ÷ ( x + a ) ]
= [ y( x + a ) + x( y + b ) ] ÷ x( x + a )
= ( yx + ay + xy + xb ) ÷ ( x² + ax )
= ( 2xy + ay + xb ) ÷ ( x² + ax )
= [ x( 2y + b ) + ay ] ÷ ( x² + ax ), which is a simplified form for ease of calculation.
The second formula, for subtracting one fraction from another, is therefore also achieved the same way, by cross multiplication, even though at the start, I had actually worked these equations out a different way, using a table of values, only for the cross multiplication to confirm them.
( y ÷ x ) + [ ( y + b ) ÷ ( x + a ) ]
= [ y( x + a ) - x( y + b ) ] ÷ x( x + a )
= [ ( xy + ay ) - ( xy + xb ) ] ÷ ( x² + ax )
= ( ay - xb ) ÷ ( x² + ax )
So these two interesting formulae will work for the subtraction and addition of any pair of fractions you can think of. All you need be aware of, is that if the numerator or denominator on one fraction differs from the other, your b and a values are the differences between the two numbers, and do not represent numbers in a fraction themselves.
Don't be so Mean
Next, let us look at what in Mathematics is known as the Geometric Mean, where, if we know then that a ÷ b = b ÷ y, then b² = ay, so that b = √(ay)
If you are not already familiar with the small numbers raised up to the right of an ordinary number as we see here with b², we shall be studying more of these later. All you need to know is that b², which is pronounced b squared, is the same as saying b times b, so that if b equalled 9, then b² would be the same as 9², or 9 × 9, which is 81. Now, back to our Geometric Mean, an example of this using numbers represented by the letters, is :
4 ÷ 10 = 10 ÷ 25 ; 10² ( = 10 × 10 = 100 ) = 4 × 25,
and the reason for this working is explained in identical fashion to the one before, by manipulating the fractions to change the subjects.
See, if b ÷ a = y ÷ b, then ay = b² For instance, 3 ÷ 9 = 1 ÷ 3, and 1 × 9 = 3²
This again works when you manipulate the fractions and change the subject, so let’s look next at adding fractions with different denominators, and see what happens. Here’s a formula from Physics to do with how light is emitted. 1 ÷ f = 1 ÷ v + 1 ÷ u
If we see this, we might want to find out what f equals, so how do we do that ? Well, 1 ÷ v + 1 ÷ u obviously equals the reciprocal of f, (1 ÷ f), so all we do is cross multiply, then flip the fraction, thus : 1 ÷ v + 1 ÷ u = ( v + u ) ÷ uv, so f itself = uv ÷ ( v + u ).
The same cross multiplication will work to manipulate any formula in order to change its subject. When we cross multiply, all we do is multiply each denominator of one fraction by the numerator of the other, add or subtract those totals within the numerator, and divide by the product of both denominators
Moving On Even Further
We continue this journey in the next Hub, The Very Next Step - Squares and the Power of Two and if You are curious, take a look at the other Hubs, The Maths They Never Taught Us - Part One, The Maths They Never Taught Us - Part Two , And then there were Three - a Study on Cubes, Moving on to Higher Powers - a First look at Exponents, The Power of Many More - more on the Use of Exponents, Mathematics - the Science of Patterns , More on the Patterns of Maths , Mathematics of Cricket , The Shape of Things to Come , Trigonometry to begin with, Pythagorean Theorem and Triplets, Things to do with Shapes, Pyramids - How to find their Height and Volume, How to find the Area of Regular Polygons, The Wonder and Amusement of Triangles - Part One, The Wonder and Amusement of Triangles - Part Two, the Law of Missing Lengths, The Wonder and Amusement of Triangles – Part Three : the Sine Rule, and The Wonder and Amusement of Triangles - Part Four : the Cosine Rule.
Also, feel free to check out my non Maths Hubs :
Bartholomew Webb , They Came and The Great New Zealand Flag
Just take a good look then see if you can come up with anything along the same lines. By all means Your comments are very welcome, as well as feedback and suggestions which would be given due credit, or indeed have a go and publishing Your ideas Yourselves, but firstly, by all means, add Your comments - it's a free Country.
Disclaimer
Any reference to any Copyright or Registered Trademark is credited as such. Some discoveries are my own, but may also have been found independently by others as Mathematics is a living language. Some information has been referenced in a number of publications, most in the public domain, as well as on Wikipedia ( copyright 2013 Wikimedia Foundation ).