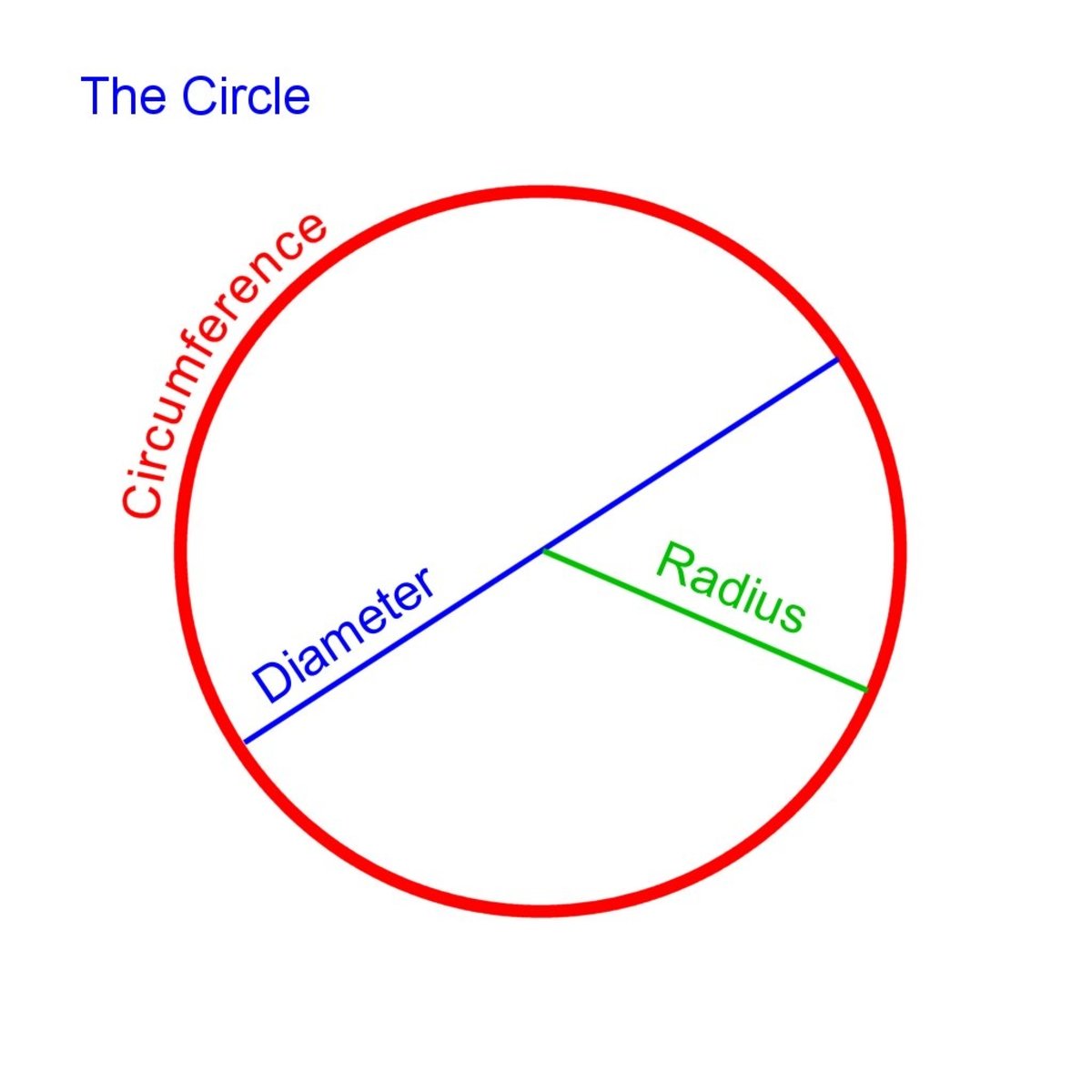
Meaning and Purpose of Mathematics

The unpredictable weather, the changing climate, and the destructive earthquake can all be understood, studied, and forecasted with the help of mathematics. The motion of the Earth around the Sun, the gravitational force between objects, and the solar energy that makes life possible are revealed, understood, and calculated with the help of the mathematics. We use mathematics to balance the budget and run the economics, to build durable and workable structures and machines, and to unlock the secret inside the atom and the origin of the Universe. Nature no longer works in its mysterious ways but in numbers that obey the rules and equations as defines in the mathematics. We invented the mathematics as we tried to understand how Nature works and how to exploit its vast hidden resources. After more than 2000 years of developments, today, mathematics is broken down into specific branches according to complexity and application.

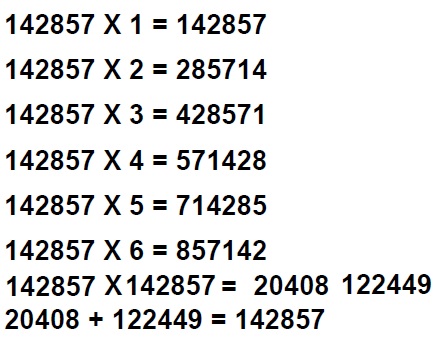
Arithmetic

Arithmetic is the most basic math that deals with simple number manipulations – addition, subtraction, multiplication, and division. It is so vital to the survival in the man-made world that it is taught starting from the grade school. Few adults will ever forget memorizing the multiplication table during those innocent years. Without the knowledge of arithmetic, a person will find it difficult to purchase things with money, to understand the passage of the exact times, and not to mention how to save money for the old age. For example,

1. If one buys 4 pounds of orange at $1 a pound (1x4=$4) and Pays $10 for the purchase,

2. One plans to save half of the money returned (10-4=$6) for old age (6/2=$3) on a weekly basis.

3. If the person is 20 years old now, by the time one is 65 (65-20=45), the person will have saved 45x52x3=$7020.

Algebra

Algebra uses variables (X, Y, A, B, etc.), expressions (X+Y, A/B, etc.), and equations (X-Y = AxB) to quantify, visualize, generalize, and eventually, solve the problems. The problem can be as simple as finding :

1. The slopping side of a right-angled triangle - C² = A² + B²), or

2. The non-intrusive attractive force between any 2 objects - F = [G x M1 x M2] /D², or

3. Mass to energy transformation – E = M x C², etc.

   With Algebra, our life is no longer full of uncertainty and based on subjective feelings. The structure of the objects found in the wild and the occurrence of the natural phenomenon all follow some forms of algebraic formulas. We are using it to lay the ground work to unlock the secrets of Nature in cold hard numbers and comprehensive equations.

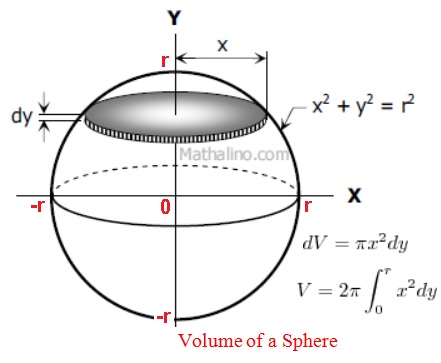
Calculus

Calculus introduces the concepts of limit, infinity, infinitesimal, integration, derivative, and function to help us find area and volume of irregularly shaped object ( ∫ f(X)dX ) and to visualize and analyze event that changes instantaneously and over times ( df(X)/dX ). To start, a function is needed to describe and represent the subject matter. It is normally a mathematical equation expressed with algebraic variables that can be referenced in one, two, or multi- dimensions.

1. f(X) denotes a function of 1 variable and describes events that occur in 2 dimensions,

   for f(X) = 4X³+2X-7, then

   ∫ f(X)dX = X⁴+X²-7X + C, for area between X=2 and X=5, ∫ f(X)dX =615 – 6 = 509

   df(X)/dX = 12X² +2X, for rate of change @X=5, df(X)/dX = 310

2. f(X,Y) denotes a function of 2 variables and describes events that occur in 3 dimensions,

   for f(X,Y) = 4X³+2Y²-7XY+3, then

   for volume between X=2 and X=5, Y=1 and Y=3,

   ∫∫ f (X,Y) dXdY =∫ (∫ [4X³+2Y²-7XY+3] dX) dY = ∫ [X⁴+2XY²-7X²Y+3X] dY

   = ∫ ( [625+10Y²-175Y+15] - [1+2Y²-7Y+3] ) dY = ∫ (636 + 8Y²-182Y) dY

   =636Y + (8/3)Y³ – 91Y² = 1161 – 543 = 618

   for rate of change @ X=2 and Y=3,

   ∂ f (X,Y)/ ∂X = 12X²-7Y = 48 – 21 = 27,

   ∂ f (X,Y)/ ∂Y = 4Y - 7X = 12 – 14 = -2,

3. f(X,Y,Z) denotes a function of 3 variables and describes events that occur in 4 dimensions,

   f(X,Y,Z) = 4X³+2Y²-7Z+3XYZ-10, etc.

Linear Algebra

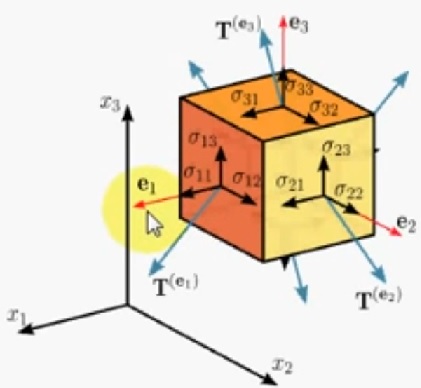
It deals with element or object that has not only a magnitude but also a direction of movement (called vector) like the wind, fluid, electric field, mountain terrain, etc. It introduces a coordinate system to study, analyze, and visualize the vector in motion and its interaction with the surroundings. The coordinate system can be two, three, to multi- dimensions. It is an invaluable tool in the formulation of the wave equation that opens a window into the inner space of the atom and the space-time continuum equation that acts as a road map to the outer space of the Universe. With the help of Linear Algebra, Einstein was able to materialize his thought experiment into concise mathematical equations that can be applied to the understandings of the Black hole and the Big Bang.

1. Δh = (dh/dx) Δx, change in Height = Gradient x Distance

   Δh(x,y) = (∂h/∂x) Δx + (∂h/∂y) Δy, for 2 dimensions

   Δh = (∂h/∂x₁) Δx₁ + (∂h/∂x₂) Δx₂ + . . . + (∂h/∂x_n) Δx_n, for n dimensions

   = ∑_n (∂h/∂x_n) Δx_n

   2. (Δs)² = (Δx) ² + (Δy) ², displacement in 2 dimensions

   (Δs)² = (Δx₁) ² + (Δx₂) ² + . . . + (Δx_n) ² , displacement in n dimensions

   = ∑_mn [δ _mn (Δx_m) (Δx_n)], δ _mn = 1 for m = n, 0 for m ≠ n

   3. Δx_m = (dx_m /dy_u) Δy_u, in curve space

   Δx_n = (dx_n /dy_v) Δy_v, in curve space

   (Δs)² = ∑_mn [δ _mn (dx_m /dy_u) (dx_n /dy_v) Δy_u Δy_v ], in curve space

   (Δs)² = G_mnΔy_uΔy_v, G_mn = metric tensor for curve space

New Frontier

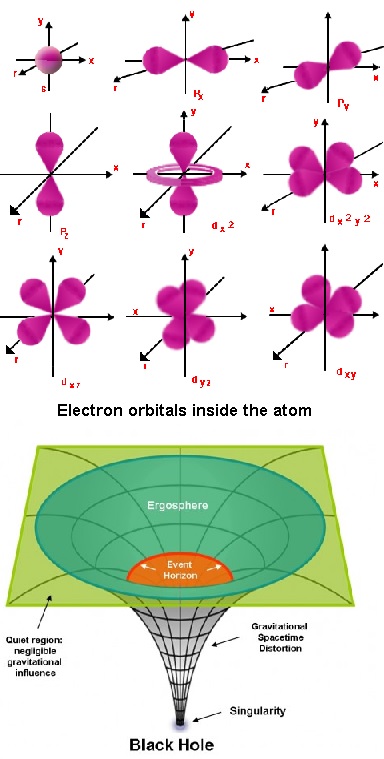
In our unstoppable and determined pursuit in the understanding of how Nature works, we have developed and accumulated a concise and detailed knowledge base – Astrology, anthropology, biology, chemistry, mathematics, physics, etc. All of them use some discipline of mathematics to assist their understandings and advancements. It is especially so in the field of Physics where mathematical equations are used to describe, analyze, and predict observable as well as undetectable phenomenon. In the study of the infinitesimal world inside the atom to the unreachable unimaginably vast world of the celestial bodies in the Universe, mathematical equations have become the primary tool to prove old theories, to formulate new insights, and to visualize bold ideas. For example:

1. The Einstein Cosmological constant – G_uv + g_uv Λ = 8πT_uv . This equation describes how the space is curved by the objects in the Universe where the constant Λ unintentional predict our expanding Universe that was once thought to be static.

2. The Schrodinger wave equation – (∂²Ψ/∂² X²) + [(8π²m/h²) x (E-V) Ψ] = 0. This equation describes how the fundamental particles behave and interact inside the atom and sets the stage for the emergence of the Quantum Mechanics.

   Mathematics allows us to use logics, reasons, and cold hard numbers to guide our thinking and endeavors in the quest of the meaning and purpose of life.