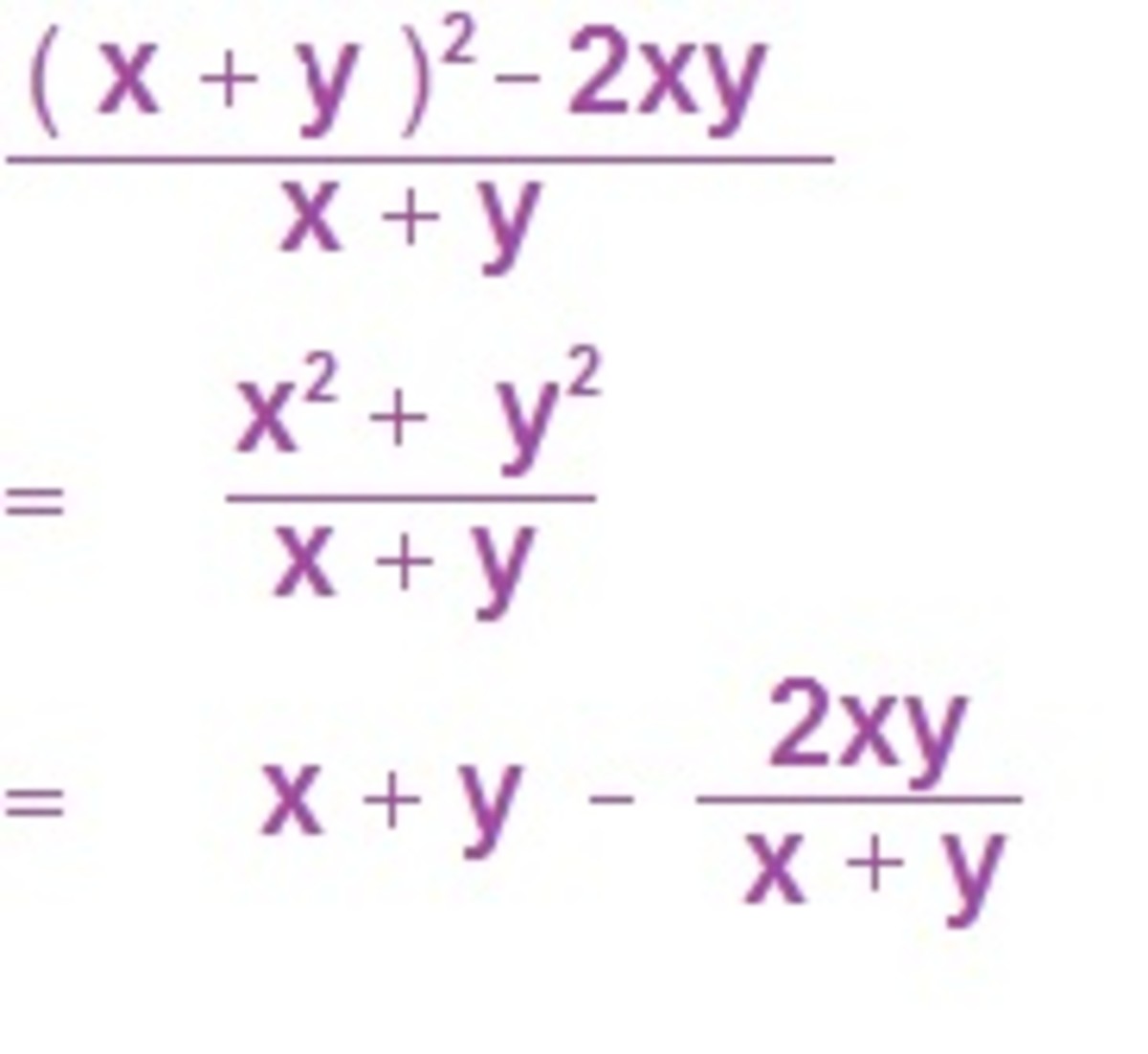The Maths They Never Taught Us - Part Two
Plus, how many Times ?
As noted in Part One of this Hub, The Maths They Never Taught Us - Part One , for the purpose of Mathematics, seeing we are only multiplying numbers without knowing what they represent, we are normally just interested in their total. An interesting thing to note is that we could actually compare the addition version of each multiplication, and see how they measure up to each other.
Thus :
5 + 5 + 5 + 5 = 4 + 4 + 4 + 4 + 4
implies
5 + 5 + 5 + 5 =
4 + 4 + 4 + 4 + 4
Let me Explain
If we pair each five with the four below it, we end up with one extra four not paired to a five, but for each of the four fives we did get to pair up, we see that the five exceeds the value of the four with which it has been paired by one. These four ones ( one for each lot of five ), add up to equal the one four left over.
To put this another way, we say we have four lots of five, to compare with five lots of four. We leave the four lots of five as it is, but we refer to the five lots of four as four lots of four plus one lot of four. If we then compare the four lots of five with the four lots of four, we get a difference of four more on the side of the four lots of five, which is equal to the one lot of four that we took out.
Now knowing this rule, that the order the factors are when multiplied makes no difference to the value of the product, is one thing, but this still leaves us with the task of having to multiply numbers together ; even large ones. Of course, don’t get me wrong. I am completely in favour of the use of calculators to make all those especially awkward, potentially tedious and complicated problems easy to solve, but not at the cost of a person having at least a reasonable ability to work out numbers, since you may not always have your battery powered adding machine with you.
My late father has always told me, how, long before he entered the freezing works, he was employed as a delivery boy, working in butchers’ and grocers’ shops. In those days, back in the good old nineteen fifties, he had to measure out and pack products, and do all his working out of weights and prices in his head and on paper, and in good old Imperial Weights and Measures, which are harder, but wholesome. He was very good at it, and always remained so. I guess he had to. After all, the modern, hand held electronic calculator didn’t come out until about 1971.
I believe it is quite satisfying and enlightening to be able to add, subtract, divide and multiply certain numbers together, in your head, especially to get an instinctive feel for numbers and how they work, and I also reckon that everyone should know their times tables ( see Multiplication table ) up to ten times ten, or at least make a reasonable attempt to learn as much of it as they can, since once these basics are mastered, the rest of the multiplication of larger numbers becomes easier, seeing that those lower numbers form the basis for all of the rest of the numbers we come across.
It is of course true that not everyone has the same ability, and multiplication and even addition is certainly hard to do, but in life some things are just that, hard, and once in a while, there is no really easy way out, and we might actually need to achieve any of our goals in life by putting in the effort, which takes considerable hard work. It is also true that there are quite a lot of people out there who do have the ability to learn all this, and yet don’t use it.
So, since I have made mention of it, let’s first of all look at the multiplication table of all numbers from one to ten, to see if we can even identify a few answers we know, as well as some of the patterns. We shall also come back to this table from time to time, as it relates to other concepts, and it would certainly serve your interests to become familiar with it. There are different types of numbers within this table, which we shall look at in good time, at The Very Next Step , And then there were Three and Moving on to Higher Powers .
Times Table From One To Ten
x
| 1
| 2
| 3
| 4
| 5
| 6
| 7
| 8
| 9
| 10
| ||
1
| 1
| 2
| 3
| 4
| 5
| 6
| 7
| 8
| 9
| 10
| ||
2
| 2
| 4
| 6
| 8
| 10
| 12
| 14
| 16
| 18
| 20
| ||
3
| 3
| 6
| 9
| 12
| 15
| 18
| 21
| 24
| 27
| 30
| ||
4
| 4
| 8
| 12
| 16
| 20
| 24
| 28
| 32
| 36
| 40
| ||
5
| 5
| 10
| 15
| 20
| 25
| 30
| 35
| 40
| 45
| 50
| ||
6
| 6
| 12
| 18
| 24
| 30
| 36
| 42
| 48
| 54
| 60
| ||
7
| 7
| 14
| 21
| 28
| 35
| 42
| 49
| 56
| 63
| 70
| ||
8
| 8
| 16
| 24
| 32
| 40
| 48
| 56
| 64
| 72
| 80
| ||
9
| 9
| 16
| 27
| 36
| 45
| 54
| 63
| 72
| 81
| 90
| ||
10
| 10
| 20
| 30
| 40
| 50
| 60
| 70
| 80
| 90
| 100
| ||
Go Forth And Multiply !
Moving right along, do you find multiplication of large numbers difficult without your calculator, or at least your slide rule ? There are some interesting techniques which can make this task easier, if you wish to calculate things in your head, or at least in your head on paper. And now, let’s look at a typical multiplication problem, to see if we can calculate using some shortcuts.
15 × 12 = ?
See, what we can actually do is break this down into a number of other problems :
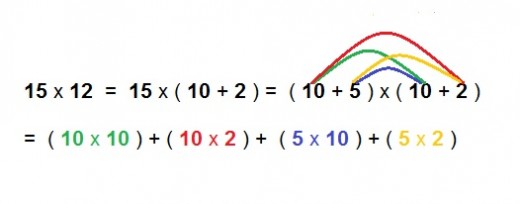
En Guard !
It is seen that the thing which happens when we multiply two two digit numbers together, is that we convert each two digit number into its value of tens and of ones, and multiply each numeral in one two digit number by each of the other numerals in the other two digit number. You may learn this technique later in Algebra as the FOIL method. This is short for FIRST, OUTER, INNER, LAST, which refers to the positions within the parentheses of the numbers we multiply, where for instance, FIRST refers to the multiplication of the two first numbers in each term. In the above example, since we are multiplying 10 + 5 by 10 + 2, then the first number in 10 + 5 is 10, as it is also in 10 + 2, as clarified below.
Illustration of how FOIL is carried out

About the Image
We see then, both from working out the addition above, and the original multiplication, that the answer to this is 180. Personally, I would have kept the number 15, and multiplied it first by 10, then by 2, and added them together to get the right answer, but it is interesting to look at it this way, just to see how numbers are multiplied together.
Also, be very aware of the relevance of those sets of parentheses, for you will, if you haven’t yet, come across what was known when I was in school as BODMAS, ( see Order of Operations ) which I mentioned slightly a while ago, and which tells you which order to work each part of this problem out in. The main thing you need know about BODMAS, is that you work out whatever is in Brackets first, then the Exponents ( those numbers raised like squared and cubed ), then Division and Multiplication, followed finally by Addition and Subtraction.
FOILED Again !
There is an easy trick to multiplying certain numbers together, especially if you do know all your Squares. Imagine you wish to find the product of 13 and 11, and don’t know how. Find the number which is halfway between them. That is twelve. All you do in this case, at least, is multiply twelve by itself, and subtract one :
12 × 12 ( = 144 ) - 1 = 143 which is the answer.
" Oh, Christopher, " you all say, " you are truly magnificent ! But pray tell, how do you do it ? "
By basic Algebra, My Precioussss. If you use the famous FOIL method I showed you before, you shall not be foiled. In this case, if you multiply two numbers with a numerical difference of two ( that is, 13 does equal 11 + 2 ), the answer is always one less than the Square of the number that comes between them, and in the sections to follow I shall show how it all works.
First of all, recall that we looked at the idea of using algebraic letters to represent mathematical variables in the previous Hub, and trusting You all understand the ideas behind this, I shall continue in that vein. Just be sure to know the difference between a letter ( either a Latin one, as used in the English Language, or a Greek), utilised as a variable, as opposed to one employed to represent a constant. In Maths we use the letter e to represent the base of the Natural Logarithm ( which we shall be looking at soon enough ), and this value for e never changes. Neither does that for pi, symbolized by the Greek letter π, which gives us the value of the ratio between the diameter and circumference of a circle, where the circumference is always π ( = 3.1415926 . . . ) times the diameter.
Whereas if we assign a value to the letter x, this value may not change within any strictly algebraic equation using that same x, but can be changed when moving on to a different problem, depending upon which value we decide to assign to the letter x. Since we can change our value of x we call it a variable. Although in some cases, the value of x can change if we are dealing with a function, but we shall look at this later. Enough to say that for a given problem if we assign a value for x, the value will stay fixed, at least for each FOIL problem.
Imagine you assign the letter x to the number between the two you wish to multiply. Therefore, the numbers either side of it can be designated as ( x + 1 ) and ( x - 1 ), respectively, and respectfully. So that, in our above example, x = 12, ( x + 1 ) = 13, and ( x - 1 ) = 11. We multiply these by the FOIL method, and get :
( x + 1 )( x - 1 ) = x² - x + x - 1,
Once again, as I explained before, this x² is just a quick way of saying x times x, and is also said as x squared. In the above equation, the -x and x cancel out, since this is the equivalent of saying x minus x, which equals zero, so we are left with x² - 1, ( which, to be clear, is x times x, minus one ), and is indeed what we ended up doing. Also, within this problem, the value of x will remain as 12, and will not change, unless we decide to designate x² - 1 as a function, which means that in general terms, whatever value x is given, ( x + 1 )( x - 1 ) will always equal x² - 1. And as noted, to make this more clear, we shall look more into this idea of functions later.
Others by way of Example
Now remember that this particular set up only works if the factors are two apart. So, let’s look at other examples of numbers which are more or less than two apart, just to get the overall idea :
17 × 18 = ? Here let us say x = 17 ; therefore ( x + 1 ) = 18, so if we expand x( x + 1 ), we get x² + x, which equals :
17² + 17 = 17 × 17 + 17 = 289 + 17 = 306, which is correct. Although if you can square 17, you might just as well, in this case at least, have been able to directly multiply 17 × 18.
Next, look at this one : 23 × 27. Here the middle number is 25, which again we call x. The other two this time are ( x + 2 ) and ( x - 2 ). When we multiply that, we end up with x² - 4, ( = x times x, minus four ), since once again the middle two terms cancel out. In fact, if you follow the pattern of this, and are multiplying x plus a number by x minus the same number, you have x times itself, or x squared, minus the number times itself, or the number squared, since the 4 of x² - 4 from above is equal to two squared, and two was the difference we had between numbers.
That of course only works if your sum and difference are the same. If not, you may have to FOIL each pair of parentheses just to be safe. All you need on top of this technique, of course, is to have memorised as many squares as you can, and as I said once before, we shall be looking at squares and similar numbers soon enough. In addition, memorising other multiplication problems from times tables is also a very good idea.
As one last example, imagine you are asked to multiply 23 by 26. We see for a start there is no middle whole number between the two. You could set x as 24.5, which will work, but then You are dealing with a whole lot of fractions, which may be harder to multiply. So say you know for a fact that 20² is 400. What you do is set x to equal 20, and thus 23 is ( x + 3 ), while 26 is of course ( x + 6 ), so you multiply :
( x + 3 )( x + 6 ) = x² + 9x + 18 = 20² + 9 × 20 + 18 = 400 + 180 + 18 = 598.
The main thing is that doing it this way does not become more awkward and complicated than doing it the other way, by multiplying the two numbers ordinarily. After all, the idea here at least is to make things easier and quicker to work out. In addition, in the above example you could have decided instead that x was equal to 21, and therefore this would make 23 = x + 2, and 26 = x + 5, and then you could multiply these out by the FOIL method. You would find :
( x + 2 )( x + 5 ) = x² + 7x + 10. Now this is different from what we had before, but remember that on this occasion, x is equal to 21, when before x had been equal to 20, and calculating this equation we get 23 by 26 equals x² + 7x + 10 = 21² + 7 x 21 +10 = 441 + 147 + 10 = 598, which again is what we wanted, so it does work, but just be aware of which number we assigned to x, and work them out from there. Also note we have turned one multiplication into the sum of in this case three others, but these may be easier ones, and this is still preferable if one knows their squared numbers at least.
I shall show some other less normal methods of calculation that the individual may or may not prefer.
GELATOSIA ( Jelly or Ice Cream ? )
Below is an example of what is known as Gelosia Multiplication. The idea is to set up a grid, with the two numbers to be multiplied together along the top and down the right hand side, respectively, and the answer once the work is performed, is to be read from the top left, in an L shape, down to the bottom right. This is in fact similar to the table used in that known as Napier’s Bones, which also allows ease of multiplication in this way. John Napier was himself the one who invented Logarithms, as we shall later see.
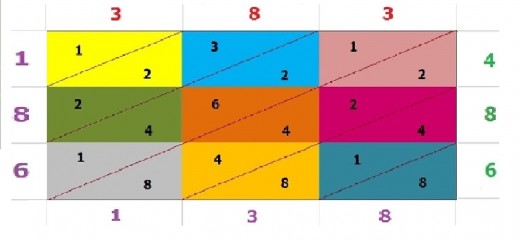
In the example, we are multiplying the numbers 383 and 486, to get the answer 186,138. What we do is set up our grid, with in this case nine spaces for the products to go into. So we multiply each of the digits in one of the factors by each of the digits in the other. For instance in the top right hand side, we have as the last digit of the multiplicand ( 383 ), the number 3, and to its right, the the first digit in the multiplier ( 486 ), the number 4. When we multiply these two our answer is 12, and you see that when we put 12 in the top right corner, inside a square, with a top right to bottom left diagonal line separating the two digits. Each product has been shaded in its own colour for clarity, while each factor of the problems at hand is of a different colour, and so is the overall answer.
We continue in this fashion, until we obtain, in this case, nine, products. Since we are only multiplying one digit numbers, our answers will only have at most two digits. To work out our answer, we then begin at the bottom right corner square, and add all the digits in each diagonal, in this grid. This is shown in the last version of the array, with all the digits to be added together lined up in top right to bottom left diagonals, with their sums at the bottom left, and the digits that are carried if the sum is above 9, to go to the top right of the diagonal above, and are counted in the next sum.
In this first square, we have the number 8 below the diagonal line. Thus we place the number 8 on its own below. Next we go to the square above, where 8 from 486 had be multiplied with the 3 out of 383 to give 24 as the product. We take the 4 from this 24 then add to it the number 1 that is on the same top right to bottom left diagonal, which itself was from the 18 obtained by the product of the 3 out of 383 and the 6 from 486, then add to this the number 8 from the 48 to the left of the 18, to give us a total of 13. We place the 3 in the answer, so that so far, the last two digits of our answer are 38, then we carry the 1 to the top right hand square, to be added with the numbers in the third diagonal up, and so on, basically adding along the diagonals from top right to bottom left. Always remember to carry the extra number if your diagonal adds to a number of two digits.
The only consideration with this method is whether it is quicker to carry out the multiplication the normal way, taking into account how long it may take to draw up a grid. The beauty of this system, though, is that instead of carrying out one big awkward multiplication, all you are doing here is a greater number of much easier ones, plus a little addition, so that the only thing you need ensure is to carry out your steps correctly, put all your numbers in the right place, and you’ll be fine.
Example of Gelosia : 383 x 486 = 186,138
The Gelosia Products Explained
Having seen the above grid for the Gelosia multiplication problem, below shows the explanations for how we arrived at the products within each individually coloured cell, by a slight rearrangement of each of the cells in the first grid.

Lining up the Sums in Obedience
In the diagram below the numbers are repositioned to show how they are added along the top right to bottom left diagonal.
They are colour coded to show how numbers each of the same colour add to the total on the bottom left.
Those digits in parentheses () indicate the tens column of the sum. This is then to be carried to the top right of the diagonal above and included in the next sum.
The colour of the asterisk * next to each carried number indicates the line it has been carried from.
Same Gelosia Table With Sums Lined Up, And Showing Positions of Carried Numbers ( in parentheses )
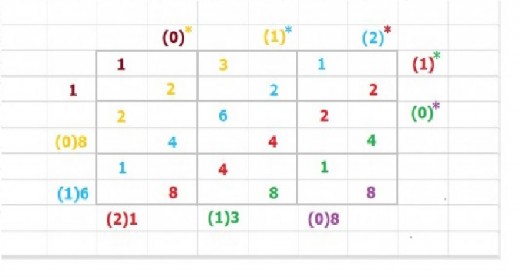

The way it works is reasonably simple. Imagine we wanted to multiply the two numbers above in question, and decided to do it the normal way. I would carry it out in the following fashion :
383 x 486 = (300 + 80 + 3) x (400 + 80 + 6)
= (300) x (400 + 80 + 6) + (80) x (400 + 80 + 6) + (3) x (400 + 80 + 6)
= (300) x (400) + (300) x (80) + (300) x (6) + (80) x (400) + (80) x (80) + (80) x (6)
+ (3) x (400) + (3) x (80) + (3) x (6) = 186,138
So, if You think about it, when we do not regard as yet the tens and hundreds columns, we are basically multiplying each digit in the first three digit number by each one in the second, and carrying the numbers above ten for each sum allows us to keep track of those tens and hundreds, so to speak.
Russian Peasant / Egyptian Style
This next method of easy multiplication is based pretty much on the work we just did with fractions, where if you double one side of an equation, you must halve the other side in order to even it out.
For example, let’s look at the problem 86 × 47.
So, if we multiply 86 by two, then in order to still get the same answer, we subsequently divide 47 by two, but with this particular process, we ignore the fractions. We then do the same to these second lot of numbers, and continue until the number we are dividing by two each time gets down to one. To work out the answer from this we only add the right hand side numbers together, that are next to the odd* numbers in the left hand column, and from this we get our answer. Thus, we end up with the following :
Russian Peasant or Egyptian Example
Russian Peasant 86 47 43* 94* 21* 188* 10 376 5* 752* 2 1504 1* 3008* 3008 + 752 + 188 + 94 = 4042 which is indeed the answer
Why Russian Peasant Works
Now the reason it works, is because, when we go from 43 to 21, we have ignored fractions, so the whole answer at that stage would be 21.5 × 188, a difference so far of 94. After this we halve 21 to give ourselves 10, instead of 10.5. The additional difference because of this second rounding down is equal to 188. The next time we halve and round away the fraction, is when we go from 5 to 2, which would have been 2.5, giving us a further discrepancy of 752.
These just happen to be the three numbers we add to our final number of 3008, to give us our total correct answer, so that by taking the three numbers next to the odd numbers, we undo the rounding error, and we take the last number, 3008, because this is what our original factor doubles to.
Now, why the numbers we need happen to be the ones occurring next to odd numbers as we go down, is because this is where we do our rounding. I can also say about this system, is that it does work, as long as you don’t mind working out twice a number one way, and half the other number rounded down to go with it.
All of this comes easier if you practise your manipulations of numbers, so that by being familiar with easier equations, harder ones do become easier to do, if only on paper.
We move away for now from the realm of multiplication to the third part of these Hubs on the Basics, but in some ways keeping with idea that results in maths can work in more than one way.
Moving On
We continue this journey in the next Hub, Part Three of this same Title, at The Maths They Never Taught Us - Part Three, and if You are curious, take a look at the other Hubs, The Maths They Never Taught Us - Part One, The Very Next Step - Squares and the Power of Two , And then there were Three - a Study on Cubes, Moving on to Higher Powers - a First look at Exponents, The Power of Many More - more on the Use of Exponents, Mathematics - the Science of Patterns , More on the Patterns of Maths , Mathematics of Cricket , The Shape of Things to Come , Trigonometry to begin with, Pythagorean Theorem and Triplets, Things to do with Shapes, Pyramids - How to find their Height and Volume, How to find the Area of Regular Polygons, The Wonder and Amusement of Triangles - Part One, The Wonder and Amusement of Triangles - Part Two, the Law of Missing Lengths, The Wonder and Amusement of Triangles – Part Three : the Sine Rule, and The Wonder and Amusement of Triangles - Part Four : the Cosine Rule.
Also, feel free to check out my non Maths Hubs :
Bartholomew Webb , They Came and The Great New Zealand Flag
Just take a good look at them, and note how interesting it all is, then see if you can come up with anything else along the same lines. By all means Your comments are also welcome, aw well as feedback and suggestions which would be given due credit, or indeed have a go and publishing Your ideas Yourselves, but firstly, by all means, add Your comments - it's a free Country.
Disclaimer
Any reference to any Copyright or Registered Trademark is credited as such, as in the previous Hub. As also previously noted, some discoveries are my own, but may also have been found independently by others. Other concepts such as Gelosia multiplication , also known as Lattice multiplication , is at least 700 years old, and Russian peasant multiplication is even older. Some information has been referenced in a number of publications, most in the public domain, as well as on Wikipedia ( copyright 2013 Wikimedia Foundation ).
- Sign In to HubPages
Login to your HubPages account