LagrangianMechanics

In order to understand the Brachistochrone problem, it has to be seen within the context of Euler's calculus of variations, Lagrange's algebraic method and the work of Bernoulli. This work is then a translation from these sometimes rigorous mathematical proofs to a language that most people can understand. Euler began with a geometric approach, but later adapted to what was viewed as Lagrange's more rigorous mathematical approach better capable of dealing with abstract concepts. Mathematics is an attempt at shorthand expression of complex ideas and a lot of symbolism borrowed mainly from the Greeks, had to be used in order to make the shorthand work. Symbols are important in order to generalize the shorthand so that it can apply to any set of variable, known and unknown to arrive at specific answers in particular special cases. Of course, to understand the shorthand, one has to understand the basic rules of mathematics and protocol of operations.

Calculus was co-invented by Newton and Leibniz to solve difficult problems and its basic idea is to break down complex things like variations or changes of time, velocity, irregular solids and irregular areas into small chunks that could be calculated more easily and then added together to arrive at a close approximation of an answer. By breaking down something like time into short units, we can see how motion is changing moment by moment. The shorter the time we take from the start to the end, is the derivative of time and this allows for greater accuracy in final calculation. However, the smaller the derivative, the more calculations are required in the summation to get the whole pattern. This is called the principle of least action and is still in use now. Calculus allowed the analysis of three dimensional space and time and has its foundation on algebra and on non-linear pre-calculus. Calculus comes in many varieties and each has its function in analysis. Calculus is sometimes integrated with geometric forms, Cartesian and Polar projections for some of the more arcane problems of modern physics and cosmology. Euler and Lagrange were both interested in solving cosmological problems and Lagrange in particular was successful. But Lagrange could not have done it without Euler’s ground breaking work on variations, which is considered the foundation of the variation of mechanics by modern physicists. It is variations that allow us to understand the rate of acceleration in free fall from the start moment and a second moment shortly thereafter. As the shortest; or least time was required, the second became the benchmark of measuring gravitational acceleration. Using observation and calculus in tandem, we can understand how fast something falls at any given moment and how far it has moved of a specific instant. Without this, we would not have something like the escape velocity rockets need to leave the Earth. Further, by using calculus, we have developed these used in algorithms in modern computing. Algorithms use a combination of calculus and computer language in order to turn static problems into visible motion. Any digital orrey or for that matter, any other problem solving program, run on a computer uses a host of calculus and computer language in unison called algorithms.

Lagrange went on to fuse his work with Newtonian mechanics then in the vogue for solving motions of the planets incorporating conservation laws of physics and symmetry. Euler also employed a technique to solve the brachistrochrone problem by breaking it down into three components. An interval of time was broken down into numerous sub-intervals of time. The original interval was then replaced by the sum or all the numerous sub intervals in a process of algebraic substitution as both were equal. Euler then employed a geometrical visualization of the whole. As we often find for something already in motion, such as in the case of planets, we have to "jump in" somewhere in the "middle" while the motion is already in occurrence. From this we can proceed forward, backward and tease out things like all the orbital elements and find out the "shape" of an orbit over a time frame of hours, days or years.

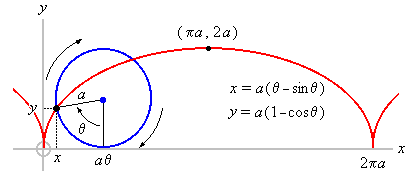
The orbital motion, speed and directions are constantly changing and the algebraic slope of a motion can be determined from between a start time and end time; usually very short, especially for rapidly moving objects. This done repeatedly can tell us if a body is speeding up or slowing down and this allows us to determine a lot about a moving body like a planet or satellite. The whole can be solved by finding the maxima and minima of all the calculations. Bernoulli’s brachistochrone problem is about finding a plane curve between two points along which a particle descends in the shortest time under the influence of gravity. A multiplicity of these plane curves are then added end to end to get the general change in the whole and this can be "smoothed out" intuitively, following the brief intervals that have been calculated and added together in a whole. In addition, the so called isoperimetric problem was solved. The isoperimetric problem finds the plane curve which encloses the greatest area for a given perimeter. This was one of the offshoots of Newton's laws of planetary motion; the basis of much of orbital mechanics outside of relativistic influences.

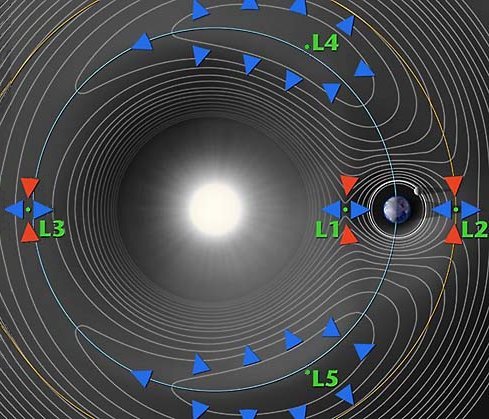
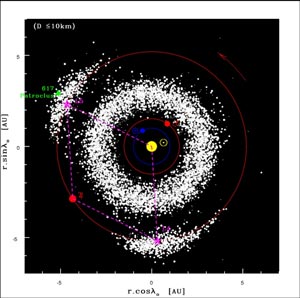
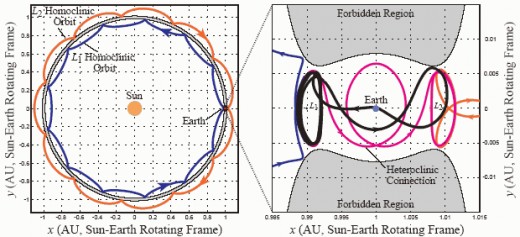
What Euler began in finding points of gravitational balance, Lagrange completed. Euler found what is now called Lagrange points 1, 2 and 3. Lagrange added points 4 and 5 and all are now named after him. As the solar system is a place of many bodies, the calculus can rapidly become unwieldy, even for the best of minds. Modern algorithms and "number crunching" computers have taken over the tedious amounts of variation, integral and summation calculations required for such monster calculus tasks. The many bodied or problem eventually went on to become known as the 'n-bodied problem', where n represents any number of bodies greater than two that are gravitationally interacting. Once more, Lagrange broke down the problem into smaller chunks and studied the Earth-Moon-Sun combination and ignored the rest. By solving for the brachistochrone problem, he could determine what the moment of gravitational influence on all three bodies together in any orbital configuration, bit by bit for the entire orbit. In the process, he discovered points in the lunar orbit around the Earth that are in gravitational equilibrium between the two. They were centered at 60 degrees ahead of and behind the moon in its orbit. This finding was later vindicated from hard observational science when asteroids were found caught in Jupiter's Lagrange points 4 and 5 in its orbit around the sun. To date, approximately 4,800 Trojan asteroids have been found orbiting both of the Lagrange points in Jupiter's orbit and have been called the Trojan and Greek camps. The lunar orbit similarly has a tiny "Trojan" at one of the Lagrange points, as does Mars' orbit around the Sun. It is thus reasonable to say that the Earth's orbit also has them. Going back to the n-bodied problem where all influences are considered, we find that the objects in orbit around Lagrange points do so due to the influence of all the other planets. In Jupiter’s case, the major influences come from Saturn and the Earth. Solving the total n-bodied problem is an immense challenge. Early results show that all orbits of all bodies around the sun produce a complex orbit called a Poincare orbit for each case. It is this that has shown us a space superhighway that we can use, exploiting the Lagrangian points and Poincare orbits.

The brachistrochrone problem then is simply a method of finding the least action of a particular motion, specifically under the influence of gravity within a short measured time. This is done a huge number of times and all the calculations are added one upon another, mapped out geometrically or defined in rigorous mathematical terms. This is crucial in understanding a lot in modern physics. To grasp the importance of this, we now measure much in quantum physics in terms of nanoseconds and shorter. Solving for the brachistrochrone problem has allowed us to develop machines such as effective rocketry and to keep space probes moving safely by planets and moons. Behind this are the important names already given above.

Reference for equations

http://faculty.matcmadison.edu/alehnen/brach/MathFest2008-Brachistochrone.html