What are the next three numbers in this series: 1, 5, 19, 49, . . .
What are the next three numbers in this series: 1, 5, 19, 49, . . .
For a bonus, what is the equation?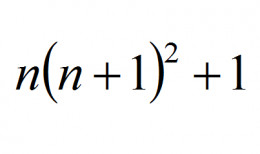
The next three numbers in the series are: 101, 181, & 295.
The equation is [n(n+1)^2]+1
Thanks for the brain teaser.- calculus-geometryposted 11 years ago
0
You can fit infinitely many equations to the points, so there are infinitely many sequences that can start with 1, 5, 19, 49. Here are some more obscure ones I found....
3^n - (n^3 - 12n^2 + 5n)/3. For n = 0, 1, 2, and 3 it gives you 1, 5, 19, and 49. For n = 4, 5, 6 the next three terms are 117, 293, 791.
2^n + (5n^3 + 12n^2 + n)/6. For n = 0, 1, 2, and 3 it gives you 1, 5, 19, and 49. For n = 4, 5, 6 the next three terms are 102, 187, 317.
Since 49 = 2*19 + 2*5 + 1*1, you could also fit the linear recursive sequence A(n) = 2*A(n-1) + 2*A(n-2) + A(n-3) to the points. Then the next three terms would be
2*49 + 2*19 + 5 = 141
2*141 + 2*49 + 19 = 399
2*399 + 2*141 + 49 = 1129
You can actually work out an explicit equation for this, but it invoves finding the roots of the polynomial x^3 - 2x^2 - 2x - 1 = 0.An answer more complicated than the problem - and enlightening!
This answer is mind boggling. I will bookmark this for further study.
Related Discussions
- 5
What answer are you guys getting for this math equation ? 2(x+19)=171-17(x-19)
by crystaalrose 13 years ago
What answer are you guys getting for this math equation ? 2(x+19)=171-17(x-19)I keep...getting 24 but in my answer key it says the answer is 6. What exactly am I doing wrong? Can someone solve it step by step ? please. Appreciated.
- 41
Average age of death for COVID-19 higher than that for natural death?
by Kyler J Falk 3 years ago
How do you feel about this statement? Personally with all the disinformation going around, such as the tit-for-tat argument around whether or not someone actually died from COVID-19 but being included in the death rate regardless, I'm having trouble formulating any clear thoughts on this COVID-19...
- 54
Could Covid 19 Numbers be False?
by Readmikenow 3 years ago
Hospitals are paid more for Covid 19 patients“So, hospitals get an extra $13,000 if they diagnose a death as COVID-19,” a widely shared meme on Facebook claimed. “And an additional $39,000 if they use a ventilator!” One post of the meme, shared by hundreds, was captioned: “And then we wonder why...
- 11
The CDC Inflated Covid fatality numbers by 1,600 percent
by Readmikenow 3 years ago
So, what is real when it comes to Covid? Can we believe what the government is telling us? Not correctly reporting numbers at this level requires effort. What would be the motivation?"CDC Inflated Covid fatality numbers by 1,600 percentA peer-reviewed study contends the...
- 10
What this figure presents?
by flysky 10 years ago
What this figure presents?
- 4
What does the number next to my "hubs" mean?
by Sydney J 12 years ago
What does the number next to my "hubs" mean?









