The Maths They Never Taught Us - Part One
The Basics
Let us begin this Article by an explanation of the the Title. When I speak of The Maths they Never Taught Us, I do not mean that teachers or the education system in any country is particularly lax, but rather that there are things in Mathematics that either were once taught, and no longer are, depending on which Country You are in, or some things that have been left out for various reasons, and I am especially looking at my own experiences in learning, which may or may not be the same as those of others. Suffice to say, that the following are certainly things we do need to know.
We thus commence our exploration into the World of Mathematics by a look at what the British television character Basil Fawlty® once said would be his wife Sybil's® specialist subject on the Mastermind (TV series)® : " the bleeding obvious ". By this I mean certain mathematical and linguistic traits we take for granted or do not even understand, where we may all get confused as to what is meant when something is said. I say the obvious, as it may even seem so to some, but these explanations are primarily for those who may not as easily grasp such concepts, with no judgment on their intelligence or ability. Perhaps we could all do with such explanations, as some things are in fact better not left unsaid.
A prominent example of what I am trying to point out is the reason why for example, the 1900s is referred to as the Twentieth Century, although it begins with the number 19, and not 20. I shall explore this kind of thing and certain others, in order to clarify these meanings. Then in the Hubs to follow I shall get into basic mathematical concepts as well as some which are often overlooked, or not fully appreciated.
So why indeed do we refer to the time we are in now as the 21st Century when we are still only in the Twenty Hundreds ? Yes, we are told that this is the time we are in, but are not always informed as to why it is referred to as such. Let us think back to the beginning of our A.D. ( Anno Domini ) era, from which we take our current dates. If we believe such, we understand that Christ was supposed to have been born on December 25th, 1 A.D., and so in countries with a Christian tradition, we take our dates from there, with those Before Christ being referred to as B.C.
As an aside which I shall look at in other Hub, if one looks through the King James Bible properly, and understands that Dionysius Exiguus, who gave us such dates, was out by a few years, it may be closer to the truth to say that the Baby Jesus was born in about September, 4 or 5 B.C., although other sources may differ. But given the dating system we do have, we then say that the years from 1 A.D. to 100 A.D. inclusive, covering a whole hundred years, make up the First Century A.D., since this is the first lot of one hundred years from the official time of Christ's Birth ( see Nativity of Jesus ).
Now this will only work if one counts all of 1 A.D. and goes through to the end of 100 A.D. This then gives another of the obvious things I am here to point out, that although the length of time from the 25 December 1 A.D. to the 25 December 100 A.D. will make 99 years, we can make up the whole century by ( arbitrarily ) deciding simply to say that the First Century A.D. will begin at the very start of the 1st January 1 A.D., just as midnight had past of the 31 December of the previous year, and this same century will last up until midnight on the 31 December 100 A.D.
So if we take each single year as it is from the very beginning of its 1st of January until midnight at the end of its 31st of December, this is one whole year, and since we are going from 1 A.D. to 100 A.D. inclusive, this is 100 separate years in total, and indeed, as noted, one whole century. Accepting this, we take the Second Century A.D. to be from the very start of the First of January, 101 A.D. to the very end of the 31st of December of 200 A.D. So it is called The Second Century A.D., even though most of its years are in the 100's.
Y not 2K, OK ?
This pattern is therefore repeated, so that the years from the beginning of Tuesday the First of January, 1901, until midnight of Friday the 31st of December, 2000, were referred to as the Twentieth Century, yet most years are in the 1900s. This brings to light an interesting issue from, if some of You can remember, say, 14 years ago, ( at the time of this writing, November, 2013 ), as 1999 drew to a close, and the term Y2K ( with reference to the Year 2000 Problem ) came more into prominence. People assumed the 21st Century and therefore the New Millennium it ushered in began at the stroke of Saturday the 1st of January, 2000, but Horn and Abbot's Trivial Pursuit™ even had as a kind of trick question, what the first day of the 21st Century would be. This was where people might have been expected to give 1st of January, 2000 as the wrong answer, but if we take our whole A.D. System as being from the very start of 1 A.D., then all subsequent years ending in a 1 will begin centuries and even decades.
Therefore, for practical purposes the Y2K Bug was assumed to attack computer systems as we clicked round to 2000, since we thought they would assume it was the same as 1900, and this made people think it was the start of the Millennium. In reality, this Millennium did not begin until Monday the 1st of January, 2001. ( A study of dates and how they work, re perpetual calendars and the ways in which the days of the week alter with the dates as years go by, will follow in another Hub ).
Related to this idea is that of decades beginning with the year ending in a 1. Now what this strictly means is that the nineteen seventies, say, did not really begin until Friday the 1st of January, 1971, and sure, that is logical and correct. But naturally, when any talks of the seventies I am sure they mean, as I do, the time from the very start of Thursday the First of January, 1970, until Auld Lang Syne on Monday 31 December, 1979, and does not exclude 1970, nor include 1980. Sure, in reality, 1980 was in fact the last year of the 1970s, but perhaps we can allow our minds a little laxitude if only on that matter, and say instead that the seventies were the inclusive time I gave, with years like 1970 and 1980 as those transitional periods into the next era, but remember that the other option is more technically valid.
Include me in
Another aspect of numbers about which we get confused, and has been mentioned here, is the idea of what I call Inclusiveness. If I mention a range of dates, say from the Fifth of January up to the Fifteenth, we might say that this covers ten days, but we would only be right if we are taking our measure from a given time on the Fifth until the very same time of day on the Fifteenth, and so the total time within that range would be ten days. But if we instead take each day in its entirety, we are dealing with a total of eleven different days. Were we rather to consider our range of time to be just past midnight as the Fifth of January begins, thereby including all of this date, right up to midnight at the very end of the Fifteenth of January, then this covers eleven days inclusive, these being the 5th, 6th, 7th, 8th, 9th, 10th, 11th, 12th, 13th, 14th and 15th.
Another matter we shall look more at later is the confusion over winning targets in Cricket. Depending on the format, basically one teams sets a total, the other tries to chase it down. Say for example that in a match where each team gets one innings, the first team scores 307 runs, so the winning target for the second team is now 308. This is the score needed to win. But to tie, they would only need this 308. Sometimes people confuse the target with the amount of runs the first team scored, and forget that the target has to be one run above the first score in order to ensure victory by scoring more runs. Sometimes one might see that with say one ball left the chasing teams needs two runs to win, and when they get only one run, they think they have lost and forget that the scores are in fact tied.
Now sometimes in cricket though, there will be the situation, in Test Matches especially, that one team has batted first, then the other. Now say the second team had a lead of 78 runs, then the first begins their second innings. Here this first are in a very slight danger of an Innings Defeat, because they now need at least these 78 runs to make the other team bat again to chase a score that has been set, but that is not very likely in these days, since teams try to avoid being bowled out for less than 78 runs, although it is not impossible. However, an Innings Defeat is much more likely if the lead was 378 runs. Some get confused like that - I have been - in this case, it is a minimum of 378 runs just to make the others bat again, not to win or tie. If they get exactly 378 runs, then the opposing team needs only one run to win, which should not be too hard. ( Incidentally, the lowest Test Innings score was by New Zealand against England at Eden Park on Friday 25th of March 1955, where NZ scored only 26 all out, and lost by an Innings and 20 runs - my late father told me years ago he remembered at the time, and it caused a bit furore then. )
Now in the case we are discussing, of a 78 run lead, as yet there is no target, since it is only the third innings, and the graphics supplied by TV will say that the second team leads by so many runs, so then that is their actual lead. The target in a sense is for the first team to wipe out the deficit and force the other team to bat again. In this case a minimum of 78 runs is required.
Say they made exactly that, then after three innings, as noted, the second team needs only one run to win, and if their batsmen go out and get one without loss, they will win by ten wickets. If instead of the first team making the necessary 78 runs to force the second one to bat again, the second team bowled the first team out for a paltry 53, this second team would win by an innings and 25 runs, because on this occasion, 78 was the overall lead, not the target, and by getting only 53, the first team fell 25 runs short. But the first team could instead have set a target by say, having trailed by these 78 runs, then ending up all out for 406, giving them an overall lead of 406 - 78 runs, which is 328 runs, and therefore a target of 329 for the second team to bat to in order to win. We in New Zealand do not assume even 26 runs is enough to avoid an innings defeat, as in 1955.
Another matter that might cause confusion is the idea of placements in say Olympic style events. Imagine a 110 yard dash, and two runners win the race - not even the microscopic evidence in the finish photo can separate them. So what about the person who comes after ? Some could argue they get a silver, but if one thinks about it, this should be wrong. Two people crossed the line before them, and we assumed all else is above board if you know what I mean, so even though they share the gold and get one gold medal each, third place is still third place, because after all, if two finish ahead of you, you would expect that, and a runner should not be rewarded more than they deserve just because two better runners could not be separated. Each of them gets the gold because they earned it, and since the third placed runner could not conceivably have done ought to make them do so, they have come in third place behind two others, so third place is what they get, and if they wanted more they shoulda run fasta.
Maybe You Can Count Your Thumb
Thinking on all these concerns, having watched TV and Movies over the years I have noted the odd arithmetical error from time to time. Now these are not just where one is confused about a range of dates, but are actually statements that simply do not add up. Right now I cannot remember a specific example, but I recall something along the lines of someone mentioning a character born a certain year, but getting their age off by two years or so, and this not due to any mistakes about Inclusiveness or anything like that - in these cases it was all quite simply bad adding.
If anyone can help me, from decades ago I recall that one of the last scenes in the original TV version of The Hitchhiker's Guide to the Galaxy, had a man spelling out a question. The answer to this was supposed to be the Meaning of Life, the Universe and Everything, which the computer Deep Thought said is 42. But in this scene the person seems to spell out " What is 9 times 7 ? ", but the answer to this is 63, ( which may even be the answer to Life, the Universe and Everything plus 21 or something ). Perhaps he had put the tile with the number 6 upside down, and made it a 9, although I think I remember he spelled out the numbers. If anyone can confirm this, this would be good. I have not seen that scene in say over 30 years. ( Yes, I am that old, and I do feel even older ).
Oh, Heck, No ! ( after all, Children might be logging on )
Let us now address the more understandable confusion we can get about ages and dates. Imagine someone has September 25th as a birthday. Indeed they do. One of my nephews, as well as Will Smith, Catherine Zeta-Jones and her husband Michael Douglas. For a good deal of the year, if one asked them what year they were born in and they gave it, then without knowing the date, one might make a false assumption about their age. Look at Smithy. He was born the same year as myself, 1968, and, as I said, on September 25, while I was brought in on January the Second. Now back in 1988, with its people wearing bad hairstyles and all, for all but one day of the year, the First of January, I was 20 years old. But Mr. Smith was 19. Yet someone may have assumed, that since he was born in 1968 and it was then 1988, that he too was twenty. So when I hear the year someone is born in, I have to consider what time of the year it is now and work out the probability they are the age they may be assumed to be. In fact, the only date we can be sure of anyone's age, based on knowing only their year of birth, is the 31st of December. This is the worst date to be born on, only in the sense of therefore not being the right age people would guess at. The best date for guessing then, is January the First.
To do with this is some confusion as to which year of life one is in. This was looked at previously with the idea of the 1900s being the Twentieth Century. In 1988, up to perhaps the end of September 24, and in fact, all the way back to September 25, 1987, Willard Carroll Smith, Jr., was in his twentieth year, which is what we are in from as soon as we turn 19 right up to before we become twenty, even though his age is given in 19. In fact, if we say a joker is 19, which we date from the day of his birth, we mean he is at least 19, which is why some young kids, in an effort to make themselves seem older, will say they are seven and a half, when called seven years of age, where they are in their eighth year. Interesting that girls will continue this trend of trying to seem older until they get there, and once they hit say 35, every successive birthday will be their 21st. Some will even seem convincing.
Dinner with Agrippina and Nero - Mushrooms, Anyone ?
Having looked at and thought about dates, and doing so also from an interest in History, I realized something that had never occurred to me. We acknowledge that the Anno Domini Years begin at what we now call the First of January, 1 A.D. ( when Jesus was perhaps in reality about three or four ), but the year before that is denoted 1 B.C. ( I understand others will differ on what they call these or even on their agreeing to our way of reckoning dates, since the Jews and Moslems ( see Muslim) each have different systems, but I am using here the dating system relevant to me and what I am comfortable with ).
So we have no Year Zero in Gregorian calendar System. ( Actually the calendar or dates as we know them were supposedly not worked out until the time of, as mentioned, Dionysius Exiguus, about 525 A.D., but as also noted he may have gotten the Birth of Christ wrong. At 1 B.C. to 1 A.D. the dates are noted as they appeared in the Julian calendar and are out by some days, until the change over to the Gregorian which we shall look at in another place, with certain explanations, as to why the Julian Calendar got out of sync with the Universe, not just being due to inaccurate setting of Christ's Birth. ) Now because there is no zero, when we work out the age of a person who was born in the B.C. era and lived into the A.D. one, we need to be careful. Since there is only one year in difference between 1 B.C. and 1 A.D., where this 1 A.D. follows right after 1 B.C., someone born in 1 B.C. would only be one year old on the same date in 1 A.D.
Extending this, if we look for example at Tiberius Claudius Caesar Augustus Germanicus, ( 1 August 10 B.C. – 13 October 54 A.D. ) who was Roman Emperor from 41 to 54, we can work out that since he was born on what we now deem to be the First of August ( birthday for all horses ), 10 B.C., then on the First of August 1 B.C., he turned nine. One year later, the First of August, 1 A.D., he would then have been ten, so that 53 years later, on the First of August 54 A.D., Claudius turned 63, which is the age given as to what he lived to. We take our age to this up to the day before our next birthday, so Willard Smith Junior was 19 up to and including the 24th of September, 1988, even though in effect he was simply a day short of twenty, and sure, one could argue he was effectively twenty years of age, but not officially, until the 25th of September, 1988, and if one wanted to be even more pedantic, not until his exact time of birth, although these days we don't normally consider that necessary, otherwise imagine me at five having to wait up to just before midnight on the 2nd of January, 1973, to blow out the candles and get my presents. Again we say when one is say 19 we mean he ( or she ) is at least nineteen. So Claudius was 63, and yet to be honest, before I was aware of how to work out these dates properly, if I had seen he was born 1 August 10 B.C., and died ( poisoned fungus, I understand, by Nero and his mother Agrippina the Younger ), 13 October 5.4. A.D., I once would have added 10 to 54 to get 64, and that would have been wrong.
Looking now at a slightly different example, let us note the man first known as Octavian, and more familiarly, Augustus ( 23 September 63 B.C. – 19 August 14 A.D.). He founded the Roman Empire, and became its first Emperor, ruling from 27 B.C. until his death in 14 A.D.. On the 23 September 1 B.C. he turned 62, so that on the 23 September 1 A.D., Augustus then made it to 63, such that if he had lived until the 23 September 14 A.D., he would be 76, but died five weeks short, and as such is recorded as having lived to be 75, by which we mean at least 75, and the rest is History. So all one need do to work out ages for a person who live from B.C. into A.D. is add the years together, but remember to subtract one as there is no Year Zero, but also be aware of what date the person was born on, and the date they then died, then one shall get the age right.
Work this one out, Sherlock !
Let us look at another aspect of how our impressions of time can tend to give us the wrong idea. Imagine two babies born about the same time in different parts of the World. First of all, Hamish McDavish, born in Invercargill on Thursday 7th of November, 2013 at 7:15 pm, New Zealand Daylight saving time, and Dudley Wright, brought into this World at 11pm Pacific Standard Time,( PST ) Wednesday the 6th of November, 2013, in Vancouver, British Columbia. Now don't go all goo goo, ladies, I made them both up. What I am trying to illustrate here is that, although young Dudley appears to be twenty and a quarter hours older, he was in fact born 45 minutes after Hamish, due simply to the difference in Time Zones between the two Dominions. This shows us that sometimes things are not always as they seem, and so when dealing with anything we need to be sure of all the details so we do not come to any wrong conclusion.
Let us look at one more way in which years of birth could give us the wrong impression. Imagine two men who lived as near neighbours in the County of Devon a very long time ago, the first, Master Jedediah Trumthwake, from 1638 – 1719, the other, Kingdom Murrycroft, from 1639 – 1718. At face value, it would appear that the older man lived about two years longer, since he was born the previous year to the other, and died in the year after he did. But did he necessarily live so much longer ? Let us look at their respective birthdays :
Jedediah : December 31st, 1638 – January 1st, 1719¸ having lived Eighty Years and One Day.
Kingdom : January 1st, 1639 – December 31st, 1718¸ having lived One Day short of Eighty Years.
So in this case, at least, the older one actually live two more days rather than two more years.
But then, if we had :
Jedediah : January 1st, 1638 – December 31st, 1719¸ having lived One Day short of Eighty Two Years.
Kingdom : December 31st, 1639 – January 1st, 1718¸ having lived Seventy Eight Years and One Day.
In effect we have added nearly two years to the older man’s time, and taken just about two years off the younger one, to give a difference in age at death of almost four years.
This is why it is important to think about how old a person really is, and what the dates of life of especially a historical person really represent, which unfortunately is not always obvious when such dates are given, as most sources only deal in years, and also when dates of historical events are given, sometimes the day of the week they occurred on, is not, and that we shall deal with in a later Hub.
It Works Either Way
You would of course have already learnt in school that for certain operations of numbers, it doesn’t actually matter in which order the numbers are put.
For Example : 4 × 5 = 5 × 4, and 4 + 5 = 5 + 4 But : 4 ÷ 5 ≠ 5 ÷ 4, while 4 - 5 ≠ 5 - 4
Now it is important to make one thing clear. The first two statements using multiplication and addition are always true, whereas with division and subtraction, the second two statements are almost always true. To show this in a general way, I shall introduce the use of letters of the alphabet to symbolize algebraic variables, which we shall also look more into in some of the Hubs to come.
With use of algebraic variables a and b to symbolize possible values that any number might take, what we mean to say, is that although a × b always equals b × a, and a + b always equals b + a, a ÷ b does not normally equal b ÷ a, and a - b does not normally equal b - a. The only exception is actually when a = b. So that for example, if a = 5, and b also = 5, then as much as 5 × 5 = 5 × 5, and 5 + 5 = 5 + 5, we see also that 5 ÷ 5 = 5 ÷ 5, and 5 - 5 = 5 - 5.
This, as stated, is the only exception where the value of both numbers on which you are performing these operations is exactly the same. Otherwise, if the two numbers are different, then, as noted, only the operations of multiplication and addition can be performed regardless of the order in which the numbers are put in the equation.
But why ? You see, it’s all very well in any subject to say that something is true simply because it is, or just because somebody says so. If you try that one on, they’ll slap your fingers with a cold, wet ruler, for in modern mathematics you must always be able to prove what you say.The best way of doing this is to show an example of what you are trying to put across, and in particular, one which is clear and accurate. Well, looking at an example of addition, this at least seems reasonably straightforward :
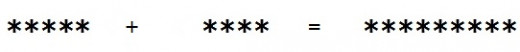
Move the Plus Sign one Space to the Left :
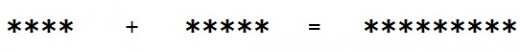
Now note that there is a total of nine asterisks, wherever the plus sign is placed, since the plus sign itself is not actually a part of the sum. That is, it is not to be counted as one of the asterisks, but is rather the actual symbol of operation. If we do the sums without it, we then get the following .
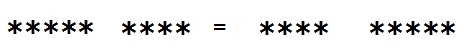
This is relatively easy to see, since you can quite simply flip the first collection of asterisks 180° over, to make it look identical to the second collection. Now, as to the matter of multiplication, we can also have a way of visualising this fact, that the order the factors are in makes no difference whatsoever to the final value of the product.

Here we have two examples of multiplication, 5 × 4 and 4 × 5, both of which equal twenty. We say five times four, because we mean to say that we are having the number five on four occasions, that is, that we are actually adding four lots of five, so that 5 × 4 is in fact the same as saying : 5 + 5 + 5 + 5, which is like saying five, four times. In much the same way, therefore, to express 4 × 5 is simply the equivalent of working out : 4 + 4 + 4 + 4 + 4. But since it would be long and sometimes very tedious, especially to add long chains of numbers together, we are taught the shortcut of multiplication.
Now as an interesting side note, just because four times five does equal five times four, this does not mean that they are always the same thing. Yes, they do give the same number, but imagine you are packing a product on an assembly line, and they want you to pack four of a product into a box, then five of these smaller boxes, each one containing the four products you’ve just packed, into a larger box. It would certainly do no good to do it the other way round, if the product only fits into the boxes a certain way, and there you are trying to ram five of goodness knows what into a space made for only four. So in some situations the arrangements of the numbers multiplied might not really matter, but in others they certainly will.
We continue this look at multiplication in the next Hub, Part Two of this same Title, at The Maths They Never Taught Us - Part Two, and if You are curious, take a look at my other Hubs, such as
The Maths They Never Taught Us - Part Three , The Very Next Step - Squares and the Power of Two , And then there were Three - a Study on Cubes, Moving on to Higher Powers - a First look at Exponents, The Power of Many More - more on the Use of Exponents, Mathematics - the Science of Patterns , More on the Patterns of Maths , Mathematics of Cricket , The Shape of Things to Come , Trigonometry to begin with, Pythagorean Theorem and Triplets, Things to do with Shapes, Pyramids - How to find their Height and Volume, How to find the Area of Regular Polygons, The Wonder and Amusement of Triangles - Part One, The Wonder and Amusement of Triangles - Part Two, the Law of Missing Lengths,
The Wonder and Amusement of Triangles – Part Three : the Sine Rule, and The Wonder and Amusement of Triangles - Part Four : the Cosine Rule.
Also, feel free to check out my non Maths Hubs :
Disclaimer
Any reference to any Copyright or Registered Trademark is credited as such, for example, mention of Fawlty Towers, which is a Trademark of BBC Television and Trivial pursuit , now owned by Parker Brothers / Hasbro . Some discoveries are my own, but may also have been found independently by others as Mathematics is a living language, and it was Ralph Waldo Emerson who described the demise of any language that does not keep growing. Some information has been referenced in a number of publications, most in the public domain, as well as on Wikipedia ( copyright 2013 Wikimedia Foundation).